非對稱共面波導彎曲結構模式轉換的研究

陳宏巍 房少軍

（大連海事大學，信息科學技術學院，遼寧 大連 116026）

引 言

共面波導（Coplanar Waveguide，CPW）由于具有易于串并聯(lián)、低損耗、低色散、集成度高等優(yōu)點被廣泛應用于微波集成電路之中［1-2］.在設計復雜電路時，共面波導彎曲結構、T型結等這些不連續(xù)電路是不可避免的［3］.然而，這些不連續(xù)部分常會在傳輸偶模信號的同時激勵起奇模信號，造成電路的傳輸損耗較高.

歸納以往的研究，抑制奇模信號在CPW彎曲結構中傳輸?shù)姆椒ㄖ饕腥N:一是在CPW的地平面上跨接空氣橋，對奇模信號形成短路，而對偶模信號影響較小［4］；二是應用上或下屏蔽平面，由于屏蔽平面與地平面的電位相同，使得奇模信號在這種情況下很難傳輸［5］；三是增加補償電路結構，例如:在共面波導較長縫隙的介質(zhì)上周期地打孔或?qū)⑤^短的縫隙設計成齒狀結構［6-8］，由于提高或者降低了一側縫隙中信號的傳輸速率，使得共面波導兩側縫隙的信號相位始終相同，也能對奇模信號起到抑制作用.然而所有這些方法都具有一定的局限性.主要體現(xiàn)在兩方面:一是由于改變了傳輸線的結構，增加了設計和制作難度；二是傳輸線結構的改變勢必改變傳輸線的特性阻抗，對于原先設計為直線的CPW，中間引入一段特性阻抗不同的傳輸線，必然會使整體的阻抗匹配惡化.需要特別指出的是，文獻［8］提出采用共面波導-非對稱共面波導（CPW-ACPW）周期結構提高CPW彎曲結構的性能，但是其原理仍屬于第三種方法，且沒有對非對稱共面波導（Asymmetric Coplanar Waveguide，ACPW）彎曲結構進行深入分析.

在過去的幾十年中，許多學者使用不同的方法分析了CPW彎曲結構.其中，Omar等人應用矩量法詳細研究了空氣橋的長度、寬度和高度對CPW彎曲結構的影響［9］；MingDong WU應用混合勢積分方程分析了無空氣橋的CPW彎曲結構［10］，詳細研究了CPW彎曲結構的模式轉換特性，指出在某些特定頻段CPW彎曲結構中模式轉換是不可避免的.然而，上述分析方法均為頻帶較窄的頻域算法，近年發(fā)展起來的時域多分辨率分析（Multi-Resolution Time Domain，MRTD）方法可以在較寬的頻帶內(nèi)保持良好的精度.并且該方法與當前流行的時域有限差分法（Finite Difference Time Domain，F(xiàn)DTD）相比，除了有較低的數(shù)值色散外，其最突出的特點是每個波長采2個點可達到FDTD每個波長10個點的精度，其空間網(wǎng)格個數(shù)只有三維FDTD的1／125.由此可見，MRTD算法對計算機資源的節(jié)省是相當可觀的［11］.

Tripathi于1974年將傳輸在非對稱平行耦合雙線中的信號分解為c模和π模信號［12］，并證明了偶模和奇模是其在平行耦合雙線對稱時的特例.而事實上CPW和ACPW分別屬于對稱的和非對稱的平行耦合雙線.本文利用時域多分辨率分析（MRTD）算法和從Y參數(shù)提取了c模、π模特性阻抗的方法，對ACPW彎曲結構模式轉換性能進行了分析.最后，提出了一種吸收π模的實驗裝置，并將其應用于CPW和ACPW彎曲結構的測試.

1 理論分析

1.1 ACPW中的c模和π模

圖1為ACPW彎曲結構端口電壓、電流的定義以及c模信號示意圖.圖中和為c模信號位于槽1和槽2的正向電壓分布，和為c模信號位于槽1和槽2的反向電壓分布.如果用、I、和表示c模信號位于槽1和槽2的正向、反向電流分布，則可以定義槽i的c模特性阻抗為

如果將公式（1）中的下標c換成π，即為π模特性阻抗定義.并且c模電壓與π模電流之間，以及π模電壓與c模電流之間有如下關系［13-14］為

式中Rc、Rπ為兩個槽的模式電壓比，如果Rc=1、Rπ=-1，則c模退化成偶模，π模退化成奇模.

圖1 端口電壓、電流和c模信號示意圖

1.2 散射矩陣

令ACPW彎曲結構上端口1處的位置坐標z=0，則端口1上的電壓和電流滿足下列方程為

式中，V11、I11、V21和I21分別為圖1所示端口1上兩個槽的電壓和電流.解方程（3）可以計算出瞬時c模和π 模的正、反向電壓和，進一步對這些信號做傅里葉變換，得到頻域的正、反向電壓和，接下來利用下列公式:

可以得到端口1歸一化c模、π模的入射波和反射波ac1、bc1、aπ1和bπ1.在端口2上做同樣的處理，可以得到端口2上歸一化c模、π模的入射波和反射波ac2、bc2、aπ2和bπ2.最終，入射波、反射波和散射矩陣的關系可以寫為

式中 Tij（i=c，π；j=c，π）為傳輸系數(shù)，Γij（i=c，π；j=c，π）為反射系數(shù).在應用 MRTD算法時，通常需要對彎曲結構計算模型激勵4次，才能計算出散射矩陣的16個未知元素.但是ACPW彎曲結構具有互易性和對稱性，因此只要對計算模型激勵2次即可.

2 數(shù)值計算與測試

2.1 數(shù)值計算結果與討論

在應用MRTD方法（選用Daubechies尺度函數(shù)為基函數(shù)）計算時，導體設為理想導體和零厚度，并使用7層的PML吸收層.其中所使用的網(wǎng)格尺寸如表1所示，p階消失矩的Daubechies尺度函數(shù)的關聯(lián)系數(shù)a（i）如表2所示［15］.計算所使用的物理參數(shù)包括:介電常數(shù)10.2，介質(zhì)厚度0.635mm，導體厚度0.035mm，中心導體寬度1.925mm，ACPW兩個槽寬分別為0.385mm和1.350mm.

表1 MRTD計算參數(shù)

表2 p階消失矩的Daubechies尺度函數(shù)的關聯(lián)系數(shù)

在MRTD計算結果的基礎上，從Y參數(shù)出發(fā)提取了相位常數(shù)、特性阻抗和模式電壓比［16］，并與Ansys公司高頻結構仿真器（High Frequency Structure Simulator，HFSS）的仿真結果進行對比.圖2為這兩種方式獲得的相位常數(shù).圖中高頻部分一致性較好，低頻部分HFSS的仿真結果偏低，這是因為，在HFSS仿真的模型中必須以理想導體作為端口邊界，抑制了π模信號的傳輸.表3為兩種方式計算的特性阻抗及模式電壓比.其中兩種方式獲得的模式電壓比及c模特性阻抗比較接近，而π模特性阻抗偏差較大，但是這并不影響對非對稱共面波導彎曲結構的分析.

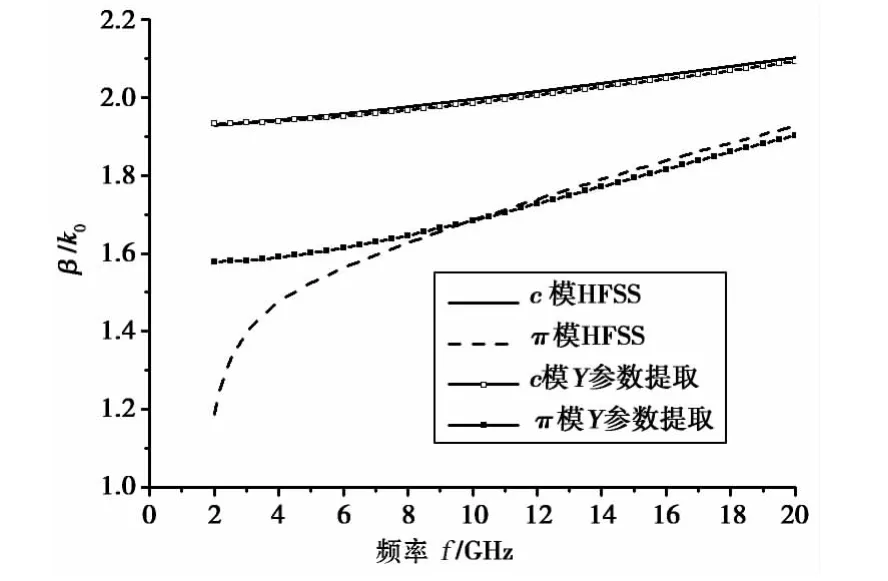
圖2 歸一化的c模和π模傳播常數(shù)

表3 特性阻抗和模式電壓比

利用公式（5）可以計算出傳輸系數(shù)隨頻率變化的曲線，如圖3所示.

圖3 ACPW彎曲結構的傳輸系數(shù)

在13GHz附近傳輸系數(shù)Tπc、Tcπ達到了最大值約-3.8dB，同時傳輸系數(shù)Tcc、Tππ減小為最小值約-3dB.這說明某一種模式信號在端口1激勵，到達端口2時，低于41.7%的能量轉換為另一種模式的信號.相比之下，偶模信號經(jīng)過CPW彎曲結構以后，在特定的頻段內(nèi)完全轉換為奇模信號［5］.從HFSS與MRTD算法仿真對比來看，2階消失矩的MRTD方法計算結果與HFSS仿真的結果較為接近.

2.2 實驗結果分析

矢量網(wǎng)絡分析儀測試端口為同軸形式的接口，然而這種接口只能傳輸TEM模，直接測試ACPW彎曲結構的結果只能是c模和π模的混合信號.因此，不能直接使用矢量網(wǎng)絡分析儀測試ACPW彎曲結構散射矩陣的各個元素.如果設定ACPW中心導體為0電位，那么對c模而言ACPW導體的電位為“-0-”；對π模而言電位為“+0-”，如圖4（a）所示.如果在兩個地平面之間跨接一個電阻，起到吸收π模信號的作用；同時，將中心導體變細使阻抗連續(xù)，確保c模信號的傳輸，如圖4（b）所示.這樣既可以測試到c模信號，又降低了π模信號的干擾.

使用Taconic CER-10板材加工制作了有吸收電阻和無吸收電阻的ACPW彎曲結構以及有吸收電阻的CPW彎曲結構，實物照片如圖5所示.三種彎曲結構的物理參數(shù)與仿真計算的物理參數(shù)一致，其中吸收電阻為80Ω，CPW的槽寬為0.7mm.

圖4 吸收π模的實驗裝置

圖5 CPW和ACPW彎曲結構的實物照片

圖6為三種彎曲結構的S參數(shù)測試曲線對比.由圖可知，ACPW彎曲結構加入吸收電阻后，｜S21｜曲線變得很平坦，說明電阻起到了對π模的抑制作用.從圖中還可以看到，ACPW彎曲結構的｜S21｜沒有在整個頻段，而是僅在較高頻段大于CPW彎曲結構的｜S21｜.這是因為在頻率較低時，電阻吸收了一部分ACPW彎曲結構c模信號能量，而對CPW彎曲結構的偶模信號影響很小；在較高頻段時，雖然仍有一部分c模信號能量被電阻吸收掉，但是ACPW彎曲結構c模信號轉換成π模信號的能量很小.所以，表現(xiàn)出在較低頻段ACPW彎曲結構｜S21｜測試結果偏低的現(xiàn)象.結合理論分析，可以確定:與CPW彎曲結構相比，ACPW彎曲結構模式間能量轉換更小.

圖6 三種彎曲結構的測試對比

3 結 論

文中提出了一種基于MRTD算法的c模、π模分解技術.通過結合MRTD算法和從Y參數(shù)提取特性阻抗的方法，推導出了4×4階的散射矩陣計算公式；在此基礎上研究了ACPW彎曲結構的模式間能量轉換現(xiàn)象.對比CPW彎曲結構，發(fā)現(xiàn)ACPW彎曲結構的模式間能量轉換較小.此外，提出了一種吸收π模的實驗裝置，對理論分析的結論進行了驗證.研究結果表明ACPW彎曲結構性能好于CPW彎曲結構，實際工程中應當用ACPW彎曲結構代替CPW彎曲結構設計微波電路.

［1］WEN C P.Coplanar waveguide:A surface strip transmission line suitable for nonreciprocal gyromagnetic device applications［J］.IEEE Trans Microwave Theory and Techniques，1969，17（12）:1087-1090.

［2］JACKSON R W.Considerations in the use of coplanar waveguide for millimeter-wave integrated circuits［J］.IEEE Trans Microwave Theory and Techniques，1986，34（12）:1450-1456.

［3］HIROTA T，TARUSAWA Y，OGAWA H.Uniplanar MMIC hybrids-aproposed new MMIC structure［J］.IEEE Trans Microwave Theory and Techniques，1987，35（6）:576-581.

［4］RIAZIAT M，ZUBECK I，BANDY S，et al.Coplanar waveguides used in 2-18GHz distributed amplifier［C］／／IEEE MTT-S International Microwave Symposium Digest.Baltimore，June 2-4，1986:337-338.

［5］OMAR A A，CHOW Y L.Coplanar waveguide with top and bottom shields in place of air-bridges［J］.IEEE Trans Microwave Theory and Techniques，1993，41（9）:1559-1563.

［6］張 卉，王均宏.奇模抑制孔縫陣列速度補償型彎曲共面波導［J］.電波科學學報，2009，24（2）:228-232.ZHANG Hui，WANG Jun Hong，Velocity compensated CPW bend for odd-mode suppression by hole array［J］.Chinese Journal of Radio Science，2009，24（2）:228-232.（in Chinese）

［7］KIM H，F(xiàn)RANKLIN-DRAYTON R.Wire-bond free techinique for right-angle coplanar waveguide bend structures［J］.IEEE Trans Microwave Theory and Techniques，2009，57（2）:442-448.

［8］李曉明，房少軍，裴 慧，等.一種非對稱共面波導相位補償彎曲結構［J］.電波科學學報，2011，26（1）:84-89.LI Xiaoming，F(xiàn)ANG Shaojun，PEI Hui，et al.Novel CPW-ACPW phase compensated structure in CPW bend［J］.Chinese Journal of Radio Science，2011，26（1）:84-89.（in Chinese）

［9］OMAR A A，CHOW Y L，ROY L，STUBBS M G.Effects of air-bridges and mitering on coplanar waveguide 90°bends:theory and experiment［C］／／IEEE MTT-S Digest.Atlanta，June 14-18，1993，823-826.

［10］WU Mingdong，DENG Shengming，WU R B，et al.Full-wave characterization of the mode conversion in a coplanar waveguide right-angled bend［J］.IEEE Trans Microwave Theory and Techniques，1995，43（11）:2532-2538.

［11］李炎紅，楊 峰，聶在平，等.基于MRTD的微帶天線的輻射分析［J］.電波科學學報，2010，25（4）:674-678.LI Yanhong，YANG Feng，NIE Zaiping，et al.Microstrip antenna radiation based on MRTD method［J］.Chinese Journal of Radio Science，2010，25（4）:674-678.（in Chinese）

［12］TRIPATHI V K.Asymmetric coupled transmission lines in an inhomogeneous medium［J］.IEEE Trans Microwave Theory and Techniques，1975，23（9）:734-739.

［13］MONGIA R K，BAHL I J，BHARTIA P，et al.U-niformly Coupled Asymmetrical Lines［M］.London:Artechhouse，1998.

［14］KRAGE M K，HADDAD G I.Characteristics of coupled microstrip transmission lines-I:Coupledmode formulation of inhomogeneous lines［J］.IEEE Trans Microwave Theory and Techniques，1970，18（4）:217-228.

［15］高強業(yè).時域多分辨方法研究及其在電磁散射中的應用［D］.南京:南京航空航天大學，2011.GAO Qiangye.A Study on the Multiresolution Timedomain Method and Its Applications to Electromagnetic Scattering Problems［D］.Nanjing:Nanjing University of Aeronautics and Astronautics.

［16］TRIPATHI V K，LEE H.Spectral-domain computation of characteristic impedances and multiport parameters of multiple coupled microstrip lines［J］.IEEE Trans Microwave Theory and Techniques，1989，37（1）:215-220.