中考數學合情推理能力的題型析解

山東省寧陽縣教育局教科研中心 尚延亮 （郵編：271400）

合情推理是從已有的事實出發，憑借經驗和直覺，通過歸納和類比等推斷某些結果.在解決問題的過程中，合情推理能產生新知識、新思想、新理論.可見，在某些情況下，教學生合情推理、教會學生猜想，遠比教學生論證推理與教證明要有意義得多.最近幾年的數學中考命題者們在這方面進行了有益而大膽的探索，試卷中出現了一些引導學生進行合情推理題目，本文從2013年各地的中考試卷中選擇部分有代表性的題目進行分析.希望對指導老師們的教學有所啟迪.

1 與數形結合思想聯系在一起，考查學生類比推理的能力

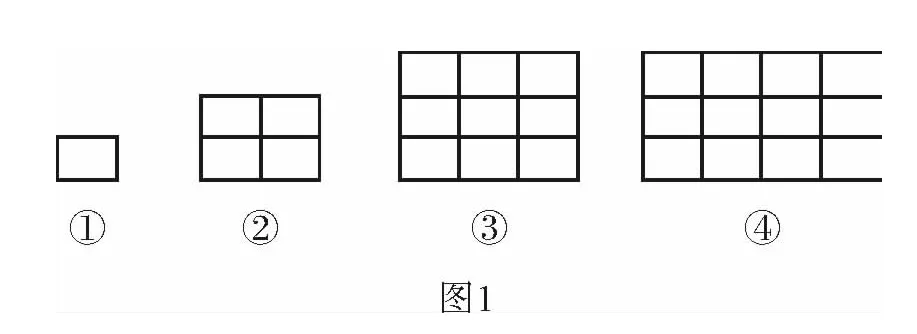
例1 （重慶卷第10題）下列圖形（如圖1所示）都是由同樣大小的矩形按一定的規律組成，其中第（1）個圖形的面積為2cm2，第（2）個圖形的面積為8cm2，第（3）個圖形的面積為18cm2，…，則第（10）個圖形的面積為（ ）.

A.196cm2B.200cm2

C.216cm2D.258cm2

解析 本題創設了一個探究圖形個數的“數形結合”的數學模型，考查了與圖形面積有關的規律探究問題，解答時，需要從簡單到復雜進行探究：圖中每一個小矩形的面積為2cm2，

第（1）個圖形的面積為2＝2×12（cm2）；

第（2）個圖形的面積為8＝2×22（cm2）；

第（3）個圖形的面積為18＝2×32（cm2）；

第（4）個圖形的面積為32＝2×42（cm2）；

……

由此，可以類比猜想得到規律：第10個圖形的面積為2×102＝200（cm2）.故選B.

點評 類比推理是根據兩個或兩類對象有部分屬性相同，從而推出它們的其他屬性也相同的一種推理.它是一種常用的合情推理形式.

從分析的過程看，本題是借助于“圖形”的形象性與直觀性逐步得到最終解決的.本題除了考察學生的類比猜想能力外，還滲透了數形結合的思想，使復雜問題簡單化，抽象問題具體化，化難為易，獲得簡便易行的成功方案.本題給我們的啟發有二：一是在數學學習中，當遇到一個問題涉及到很多或無窮多情形時，我們可以從問題的簡單情形或特殊情形入手，通過簡單情形或特殊情形的試驗，從中發現一般規律或作出某種猜想，從而找到解決問題的途徑.二是在教學中，千萬不要就知識點而講知識點，一定要把這些“顯知識”背后所“隱含”的數學思想揭示出來.做到用數學思想方法來“統領”知識點，以達到優化知識結構的目的，因為只有這樣被“優化”起來的知識結構才具有生命力和創造性.

2 在算式的計算中，考查學生歸納猜想規律的能力

例2 （山東省濱州卷第18題）觀察下列各式的計算規律過程：

5×5＝0×1×100＋25，

15×15＝1×2×100＋25，

25×25＝2×3×100＋25，

35×35＝3×4×100＋25，

……

請猜測，第n個算式（n為正整數）應表示為＝________.

解析 本題以簡單的整數計算為載體，以考查學生歸納猜想的能力為主.觀察給定的4個算式可以發現，等式的左邊都是［10（n－1）＋5］×［10（n－1）＋5］，等式的右邊都是（n－1）×n×100＋25，即100n（n－1）＋25，所以第n個算式（n為正整數）應表示為［10（n－1）＋5］×［10（n－1）＋5］＝100n（n－1）＋25.

點評 歸納推理是從特殊到一般的推理，歸納推理是一種合情推理.給定幾個代數計算式子，在計算的過程中通過歸納、猜想得到有關的規律，然后用代數變形的方式求某個式子的值或證明猜想的正確性，并利用歸納得到的規律解答給定的問題是一種常見的題型，解答這樣的問題需要較強的觀察能力、分析判斷能力、類比歸納等能力.在教學過程中，教師應結合具體的教學內容，經常設計一些類似的題目讓學生去分析和思考，學生的歸納猜想能力，必將得到較大的提高.

3 考查學生用統計的知識進行估算的能力

例3 （廣東卷第20題）某校教導處為了解該校七年級同學對排球、乒乓球、羽毛球、籃球和足球五種球類運動項目的喜愛情況（每位同學必須且只能選擇最喜愛的一項運動項目），進行了隨機抽樣調查，并將調查結果統計后繪制成了如表1和圖2所示的不完整統計圖表.

（1）請你補全下列樣本人數分布表（表1）和條形統計圖（圖2）；

（2）若七年級學生總人數為920人，請你估計七年級學生喜愛羽毛球運動項目的人數.

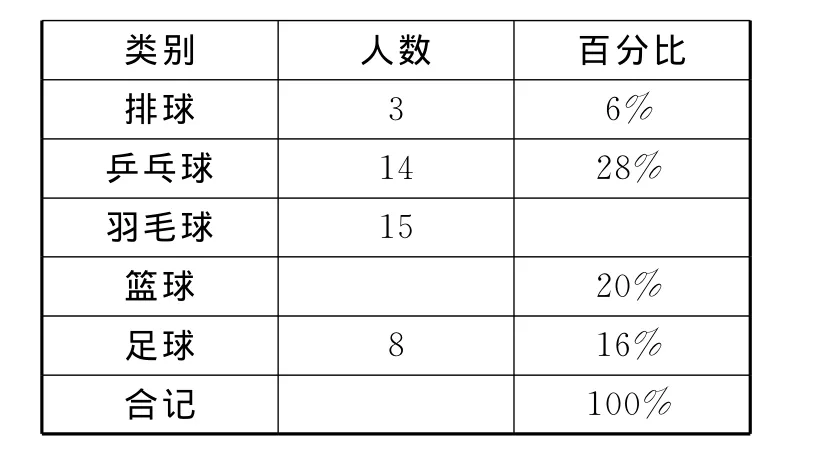
表1 樣本人數分布表

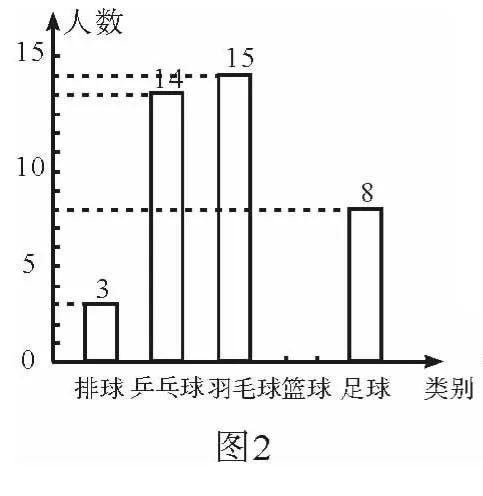
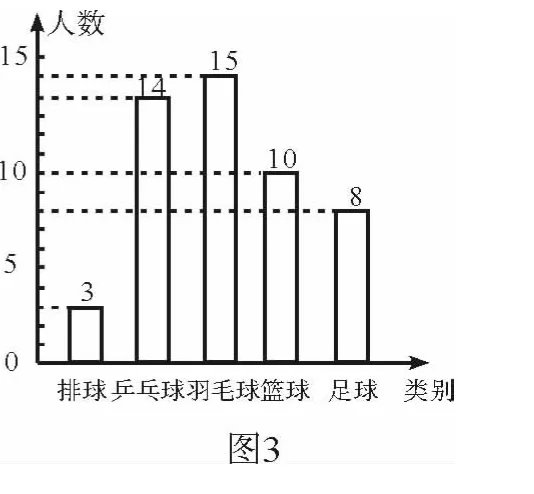
解析 （1）羽毛球占的百分比為100%－6%－28%－20%－16%＝30%，調查的人數為15÷30%＝50.所以喜歡籃球的人數為50×20%＝10.補全條形統計圖如圖3所示.（2）用樣本估計總數，得920×30%＝276（人）.即七年級學生喜愛羽毛球運動項目的約有276人.

點評 統計推理是用樣本的資料對總體的某些性質進行估計或推斷的不完全歸納推理.統計推理是從樣本到總體的推理，是一種常用的統計推理.

本題以學生感興趣球類運動進行調查為載體，得到了一些基本數據，主要考察同學們對基本統計概念的理解情況，對給定樣本數據進行處理的能力以及用樣本屬性估計總體屬性的能力.要求同學們能掌握這些概念和計算方法，正確理解樣本數據的特征，能根據計算結果作出準確的判斷.用樣本估計總體是中考對“統計初步”知識考查的題型之一，求解的方法是用總體乘以考察對象在樣本中所占的比例.類似這樣的問題對于培養學生“通過分析數據作出判斷”的能力是非常有益的.

4 在解答探索型問題的過程中，考查學生的合情推理能力

例4 （云南省八地市卷23題）如圖4，四邊形ABCD是等腰梯形，下底AB在x軸上，點D在y軸上，直線AC與y軸交于點E（0，1），點C的坐標為（2，3）.

（1）求A、D兩點的坐標；

（2）求經過A、D、C三點的拋物線的函數關系式；

（3）在y軸上是否存在點P，使△ACP是等腰三角形？若存在，請求出滿足條件的所有點P的坐標；若不存在，請說明理由.

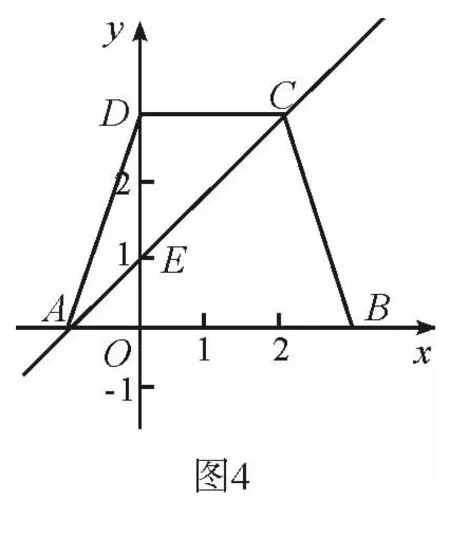
分析 （1）根據E、C兩點的坐標求直線EC的解析式，進而求出點A的坐標，由點C的坐標可得到點D的坐標.（2）根據A、D、C三點的坐標，用待定系數法求出拋物線的解析式.（3）觀察圖形，可以猜想到在y軸上存在點P，使△ACP是等腰三角形.而且這樣的點P有多個.

解 （1）、（2）省略.

（3）存在.

①作線段AC的垂直平分線，交y軸于點P1，交AC于點F，如圖5所示.

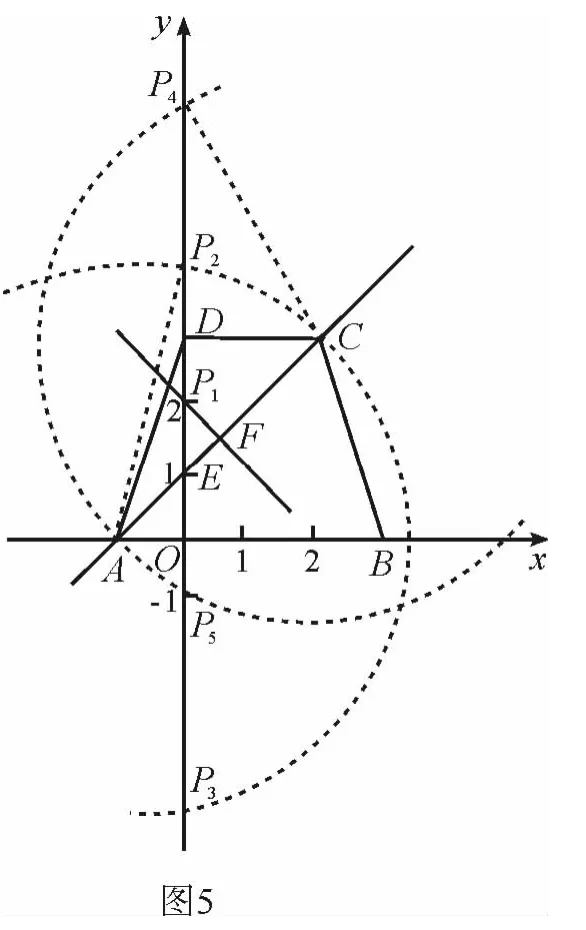
由OA＝OE，△OAE為等腰直角三角形，∠AEO＝45°，

求得 ∠FEP1＝∠AEO＝45°，所以△FEP1為等腰直角三角形.

②以點A為圓心，線段AC長為半徑畫弧，交y軸于點P2、P3.可求得圓的半徑長AP2＝AC＝3.連接AP2，則在Rt△AOP2中，

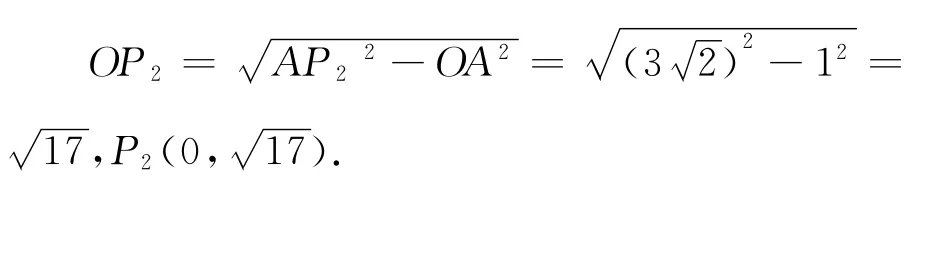
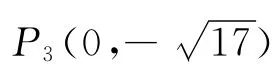
③以點C為圓心，線段CA長為半徑畫弧，交y軸于點P4、P5，則圓的半徑長CP4＝CA＝3，在Rt△CDP4中，CP4＝ 3，CD＝2，，

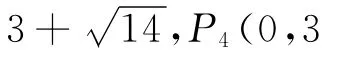
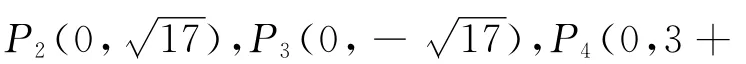
點評 本題是以三角形為載體的探索型問題.所謂探索型問題就是問題的條件或結論不直接給出，需要經過觀察、分析、分類、推理、化歸、特殊化、一般化、數形結合及猜想等一系列的探索活動，才能完成解答.解答這樣的問題，需要學生具有一定的閱讀理解能力，比較強的綜合分析與判斷猜想能力.

就本題而言，前兩問比較容易，第三問是需要探索的問題，解答的關鍵在于能憑借直觀猜想到存在這樣的點P使△ACP是等腰三角形，然后通過作圖探究點P的坐標.

總之，我們在教學中要夯實基礎知識、滲透常見的思想方法，通過分析、綜合，把所學的知識序列化、結構化.養成勤于思考、善于猜想的良好習慣，強調、重視論證推理的同時，強化合情推理的教育.精心設計教學，結合具體的教學內容，對教學內容進行二次改造，按照“問題情境—建立模型—求解驗證”的思路引導學生進行觀察、實驗、分析、比較、聯想、類比、歸納素材，以培養學生的數學猜想意識、猜想習慣、猜想能力.讓同學們在經歷觀察、試驗、猜測、驗證、推理與交流的過程中，體驗數學知識的形成過程.