平面幾何知識(shí)解決2013年高考解析幾何問題的六個(gè)切入點(diǎn)

福建省寧德市民族中學(xué) 鄭一平 （郵編：355000）

解析幾何是高中數(shù)學(xué)的重點(diǎn)內(nèi)容，也是高考考查的重要內(nèi)容之一.它的特點(diǎn)是用代數(shù)方法研究解決幾何問題，關(guān)鍵是用“數(shù)形結(jié)合”的思想把幾何問題轉(zhuǎn)化為代數(shù)問題.尤其是新課程改革增加了平面向量與導(dǎo)數(shù)之后，向量、導(dǎo)數(shù)與解幾的交匯更成為高考的熱點(diǎn)問題之一.這類問題涉及知識(shí)面廣、綜合性強(qiáng)、題目新穎、靈活多樣，有時(shí)解題過程繁雜，許多學(xué)生經(jīng)常出錯(cuò).實(shí)際上涉及解析幾何問題若能充分挖掘問題條件中隱含的幾何特征，利用平面幾何知識(shí)去解決，則能化難為易、化繁為簡，收到意想不到的效果.下面從2013年高考試題談平面幾何在解析幾何中的應(yīng)用時(shí)的六個(gè)切入點(diǎn).

1 以圓冪定理為切入點(diǎn)

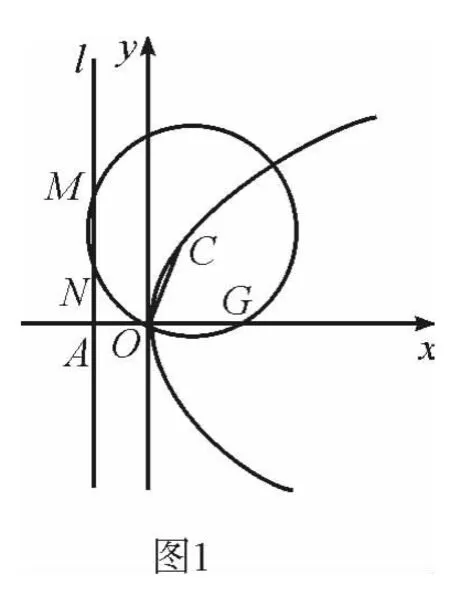
例1 （2013年福建高考文科試題）如圖1，拋物線E∶y2＝4x的焦點(diǎn)為F，準(zhǔn)線l與x軸的交點(diǎn)為A.點(diǎn)C在拋物線E上，以C為圓心，｜OC｜為半徑作圓，設(shè)圓C與準(zhǔn)線l交于不同的兩點(diǎn)M、N.

（I）若點(diǎn)C的縱坐標(biāo)為2，求｜MN｜；

（II）若｜AF｜2＝｜AM｜·｜AN｜，求圓C的半徑.

分析與略解 本題主要考查拋物線的方程、圓的方程與性質(zhì)、直線與圓的位置關(guān)系等基礎(chǔ)知識(shí).問題（1）比較簡單.問題（2）根據(jù)條件圓心C在拋物線上且過原點(diǎn)，按常規(guī)思路有標(biāo)準(zhǔn)答案中的解法：

（Ⅰ）拋物線y2＝4x的準(zhǔn)線l的方程為x＝－1，由點(diǎn)C的縱坐標(biāo)為2，得點(diǎn)C坐標(biāo)（1，2），所以點(diǎn)C到準(zhǔn)線l的距離d＝2，又｜CO｜＝.所以

（Ⅱ）抓住圓的幾何特征結(jié)合垂徑定理，從圓冪定理為切入點(diǎn)有下列簡潔解法：

設(shè)圓C與x軸交于不同的兩點(diǎn)O、G.由圓冪定理知：｜AO｜·｜AG｜＝｜AM｜·｜AN｜.

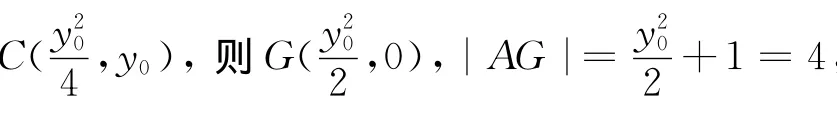
評析 涉及拋物線與圓的位置關(guān)系問題，關(guān)鍵要抓住圓心在拋物線上、圓過原點(diǎn)這些幾何特征，結(jié)合垂徑定理和根與系數(shù)關(guān)系得問題解.方（II）根據(jù)條件抓住幾何特征通過圓冪定理解決，顯然比標(biāo)準(zhǔn)答案所給的方法簡單明了，關(guān)鍵就是充分利用了圓的幾何性質(zhì)化難為易、化繁為簡，收到事半功倍的效果.下面再舉數(shù)例說明：

2 以平面幾何中面積比、線段比為切入點(diǎn)

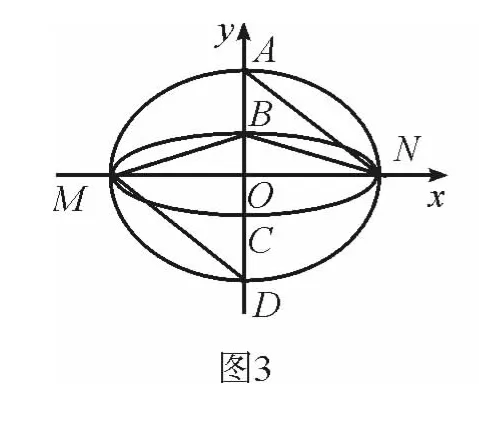
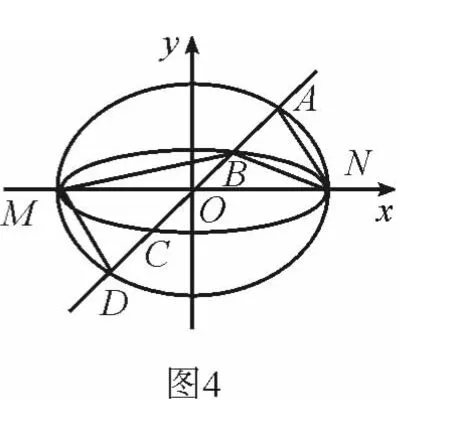
例2 （2013年湖北高考試題）如圖2，已知橢圓C1與C2的中心在坐標(biāo)原點(diǎn)O，長軸均為MN且在x軸上，短軸長分別為2m、2n（m＞n），過原點(diǎn)且不與x軸重合的直線l與C1、C2的四個(gè)交點(diǎn)按縱坐標(biāo)從大到小依次為A、B、C、D.記λ＝m，△BDM和△ABN的面積分別為S1和S2.

（Ⅰ）當(dāng)直線l與y軸重合時(shí)，若S1＝λS2，求λ的值；

（Ⅱ）當(dāng)λ變化時(shí)，是否存在與坐標(biāo)軸不重合的直線l，使得S1＝λS2？并說明理由.

分析與略解 根據(jù)條件涉及線段的比以及三角形面積問題，因此抓住圖形間的幾何關(guān)系從線段成比例為切入點(diǎn)思考比較佳.

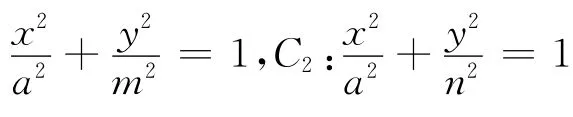
故當(dāng)直線l與y軸重合時(shí)，若S1＝λS2，則λ＝＋1.

解法2 如圖3，若直線l與y軸重合，則｜BD｜＝｜OB｜＋｜OD｜＝m＋n，｜AB｜＝｜OA｜－｜OB｜＝m－n.

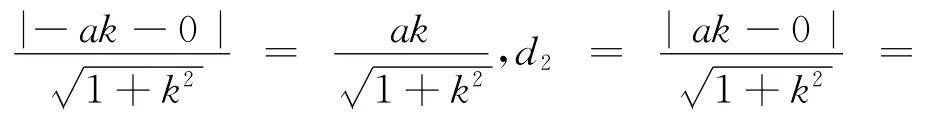
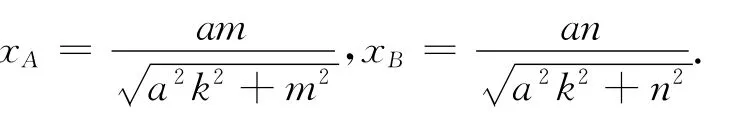
根據(jù)對稱性可知xC＝－xB，xD＝－xA，于是

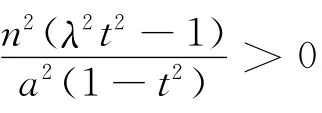
解法2 如圖4，若存在與坐標(biāo)軸不重合的直線l，使得S1＝λS2.根據(jù)對稱性，

不妨設(shè)直線l：y＝kx（k＞0），點(diǎn)M（－a，0），N（a，0）到直線l的距離分別為d1、d2，則

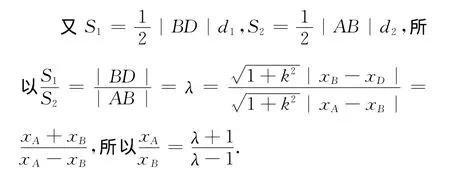
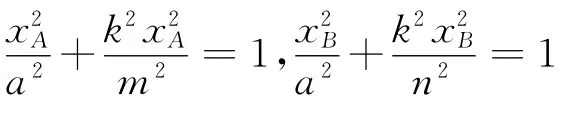
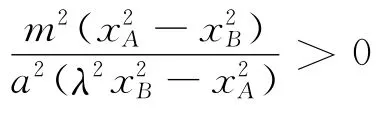
評析 本題若能通過條件結(jié)合圖形抓住三角形面積與邊或高的關(guān)系，利用比例推理計(jì)算求得結(jié)果，過程涉及點(diǎn)到直線距離和弦長等公式的應(yīng)用，通過圖形中的幾何特征的挖掘發(fā)現(xiàn)解題思維突破口是解題的關(guān)鍵.

3 以兩圓圓心距與兩半徑間的位置關(guān)系為切入點(diǎn)

例3 （2013年高考新課標(biāo)卷I）已知圓M：（x＋1）2＋y2＝1，圓N∶（x－1）2＋y2＝9，動(dòng)圓P與M外切且與圓N內(nèi)切，圓心P的軌跡為曲線C.

（Ⅰ）求C的方程；

（Ⅱ）l是與圓P，圓M都相切的一條直線，l與曲線C交于A，B兩點(diǎn)，當(dāng)圓P的半徑最長時(shí)，求｜AB｜.

分析與略解 由已知得圓M的圓心為M（－1，0），半徑r1＝1，圓N的圓心為N（1，0），半徑r2＝3.設(shè)動(dòng)圓P的圓心為P（x，y），半徑為R.

（Ⅰ）由圓P與圓M外切且與圓N內(nèi)切1即｜PM｜＋｜PN｜＝（R＋r1）＋（r2－R）＝r1＋r2＝4，由橢圓的定義可知，曲線C是以M、N為左右焦點(diǎn)，長半軸長為2，短半軸長為的橢圓（左頂點(diǎn)除外），其方程為

（Ⅱ）對于曲線C上任意一點(diǎn)P（x，y），由于｜PM｜－｜PN｜＝2R－2≤2，即R≤2，當(dāng)且僅當(dāng)圓P的圓心為（2，0）時(shí)，R＝2.所以當(dāng)圓P的半徑最長時(shí)，其方程為（x－2）2＋y2＝4，當(dāng)l的傾斜角為90°時(shí)，l與y軸重合，可得｜AB｜＝2.

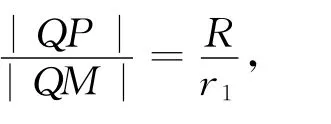
評析 涉及圓與圓、圓與直線位置關(guān)系問題抓住圓的幾何特征，結(jié)合垂徑定理、點(diǎn)線距離、弦長公式等溝通條件與結(jié)論間的關(guān)系是解決問題的關(guān)鍵.

4 以向量的幾何意義為切入點(diǎn)

例4 （2013年上海市春季高考試題）已知拋物線C：y2＝4x的焦點(diǎn)為F.

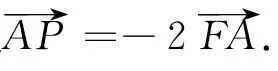
（2）在x軸上是否存在點(diǎn)Q，使得點(diǎn)Q關(guān)于直線y＝2x的對稱點(diǎn)在拋物線C上？如果存在，求所有滿足條件的點(diǎn)Q的坐標(biāo)；如果不存在，請說明理由.

分析與略解 由條件直接利用向量的幾何意義求解.（1）設(shè)動(dòng)點(diǎn)P的坐標(biāo)為（x，y），點(diǎn)A的坐標(biāo)為（xA，yA），則＝ （x－xA，y－yA），因?yàn)镕的坐標(biāo)為（1，0），所以＝ （xA－1，yA），由＝－2得（x－xA，y－yA）＝－2（xA－1，yA）.

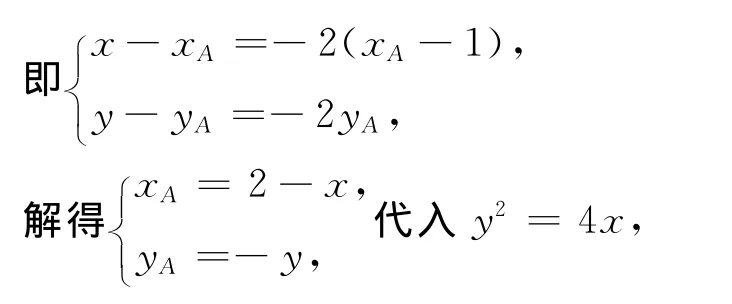
得到動(dòng)點(diǎn)P的軌跡方程為y2＝8－4x.

（2）設(shè)點(diǎn)Q的坐標(biāo)為（t，0）.點(diǎn)Q關(guān)于直線y＝2x的對稱點(diǎn)為Q′（x，y），

若Q′在C上，將Q′的坐標(biāo)代入y2＝4x，得4t2＋15t＝0，即t＝0或t＝－.所以存在滿足題意的點(diǎn)Q，其坐標(biāo)為（0，0）和（－，0）.

5 以特殊三角形的性質(zhì)、幾何特征為切入點(diǎn)

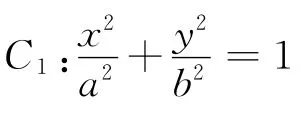
（Ⅱ）記直線AP、BP、AQ、BQ的斜率分別是k1、k2、k3、k4，求證：k1·k2＋k3·k4為定值；

（Ⅲ）過Q作垂直于x軸的直線l，直線AP、BP分別交l于M、N，判斷△PMN是否可能為正三角形，并說明理由.

分析與略解 本題考查直線、橢圓、雙曲線等基礎(chǔ)知識(shí)，考查運(yùn)算求解能力和探究能力，數(shù)形結(jié)合思想、化歸與轉(zhuǎn)化思想.

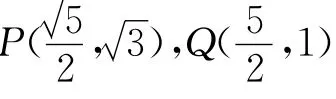
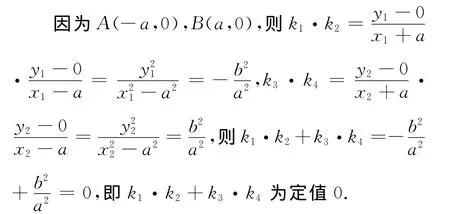
（Ⅲ）解法1 由條件假設(shè)△PMN為正三角形，下面分點(diǎn)P在x軸上方和下方兩種情況：

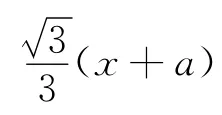
綜合上述，當(dāng)a＝且點(diǎn)P為橢圓的頂點(diǎn)（0，b）或（0，－b）時(shí)，△PMN為正三角形.

解法2 分析條件中隱含的幾何特征，考慮用等腰三角形兩底角相等幾何性質(zhì)處理：假設(shè)△PMN為正三角形，則 ∠MPN＝ ∠PMN＝60°，又MN⊥x軸，則 ∠PAB＝30°，∠PBA＝30°，即ΔPAB為等腰三角形.

綜合上述，當(dāng)a＝且點(diǎn)P為橢圓的頂點(diǎn)（0，b）或（0，－b）時(shí)，△PMN為正三角形.

評析 顯然問題（III）的解法2過程直觀簡潔，避免了分類討論和計(jì)算.關(guān)鍵就在于抓住了等腰三角形的幾何特征.

6 以圓錐曲線的幾何意義為切入點(diǎn)

例6 已知?jiǎng)訄AA經(jīng)過點(diǎn)B（1，0），且和直線x＋1＝0相切.（1）求圓心A的軌跡E方程；（2）設(shè)點(diǎn)P（x0，y0）為曲線E上的任意一點(diǎn)，點(diǎn)M的坐標(biāo)為（x0＋2，0），過點(diǎn)M作直線PB的垂線，垂足為N，當(dāng)x0變化時(shí)，線段PN的長度是否為定值？若是，請寫出這個(gè)定值，并證明你的結(jié)論；若不是，請說明理由.

分析與略解 本小題主要考查拋物線的標(biāo)準(zhǔn)方程與性質(zhì)、直線的方程及其位置關(guān)系、點(diǎn)到直線的距離公式等基礎(chǔ)知識(shí)，考查推理論證能力、運(yùn)算求解能力，考查函數(shù)與方程思想、化歸與轉(zhuǎn)化思想、分類與整合思想.

（I）解法1 （定義法）依題意，由拋物線定義知，軌跡E是以B（1，0）為焦點(diǎn)，直線x＝－1為準(zhǔn)線的拋物線，所以軌跡E的方程是y2＝4x.

所以軌跡E的方程是y2＝4x.

（II）線段PN的長度為定值2，證明如下：

解法1 當(dāng)x0＝1時(shí)，點(diǎn)P（1，±2），PB⊥x軸，點(diǎn)N與點(diǎn)B重合，｜PN｜＝｜PB｜＝2.

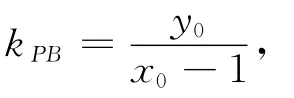
綜上，線段PN的長度為定值2，

綜上，線段PN的長度為定值2.

解法3 （幾何法）當(dāng)x0＝1時(shí)，點(diǎn)P（1，±2），PB⊥x軸，點(diǎn)N與點(diǎn)B重 合，｜PN｜＝｜PB｜＝2.當(dāng)y0＝0時(shí)，點(diǎn)P（0，0），點(diǎn)M（2，0），點(diǎn)N與點(diǎn)M重合.｜PN｜＝｜PM｜＝2.當(dāng)x0≠1且y0≠0時(shí)，過點(diǎn)P作PH⊥x軸于H，則｜MH｜＝2.

因?yàn)椋黀B｜＝x0＋1，｜MB｜＝x0＋1，，所以｜PB｜＝｜MB｜，所以RtΔPBH≌RtΔMBN.得｜BH｜＝｜BN｜，因此｜PN｜＝｜MH｜＝2.

綜上，線段PN的長度為定值2.

以上可以看出，平面幾何在解析幾何中有著廣泛的應(yīng)用，在解題中要有幾何意識(shí)，善于挖掘條件中隱含的幾何因素，結(jié)合有關(guān)知識(shí)去解決.