探索四面體的余弦定理案例及思考

浙江省溫州市溫州中學 劉旭飛 （郵編：325014）

這是筆者在市優質課評比中的課題——平面與空間中的余弦定理，它是承接普通高中課程標準試驗教科書選修2－2第二章2.1節《合情推理和演繹推理》后閱讀與思考的內容.它主要將三角形與四面體類比，由三角形余弦定理類比猜想得到四面體的余弦定理，同時由證明三角形余弦定理的方法類比得到證明四面體的余弦定理的方法.為什么要這么證？又是如何想到這種證法的？筆者認為，關注探究式教學的自然性、合理性，引導學生數學思維的自然形成、發展和深化，是我們一線教師急需關注的.現將課堂教學過程整理如下，與大家交流.

1 引入

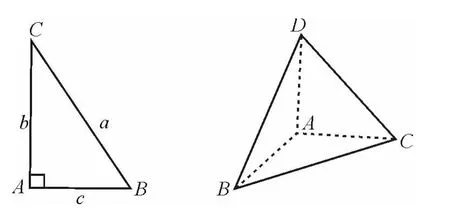
黑板上畫一個三角形.

教師：大家請看，這是平面里的三角形，在空間里選擇什么圖形作為它的類比對象呢？

學生：四面體.

教師：直角三角形呢？（學生暫時無法說出）

教師：直角三角形由平面直角坐標系中的原點、x軸上一點、y軸上一點構成.（黑板演示）

學生：直角四面體（在某一個頂點處三條棱兩兩垂直的四面體，叫直角四面體），可以把直角四面體放在空間直角坐標系中.

教師：很好，把兩個類比對象的共性理解得越清楚，類比的結論的可靠性就越好.

教師：不管是二維還是三維的幾何圖形都是由基本元素組成.下面我們看看這兩個圖形元素之間的對應.（引導學生完成下表）

2條直角邊和一條斜邊 3個“直角面”和1個“斜面”_3條邊的長度a，b，c 4個面的面積SA，SB，SC，S D_________∠A＝90° ∠BAC＝∠BAD＝∠CAD＝90°

記S＊為頂點＊所對三角形的面積.

教師：從二維平面到三維空間的類比，通常可抓住幾何要素的如下對應關系：線與面；邊長與面積；面積與體積；角與二面角；……

2 直角三角形與直角四面體類比

2.1 類比直角三角形的射影定理，猜想直角四面體的射影定理

教師：在直角三角形ABC中，過A作BC的垂線交BC于D（如圖1），類比這個過程，該在直角四面體中作什么？

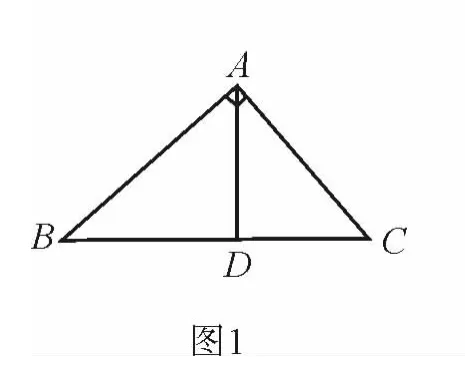
學生：過A作平面BCD的垂線交平面BCD于O（如圖2）.

教師：很好，由圖1可得：BA2＝BD·BC，這是直角三角形的射影定理，類比到直角四面體有什么結論呢？

教師：這就是直角四面體的射影定理，根據三垂線定理和面積公式易證，留給同學們課后完成.

2.2 類比直角三角形的勾股定理，猜想直角四面體的勾股定理

教師：由圖1有：AC2＝CD·BC，與BA2＝BD·BC相加可得：AC2＋AB2＝BC2，這就是直角三角形的勾股定理，能否類比到直角四面體呢？

教師：這就是直角四面體的勾股定理，怎么證明？

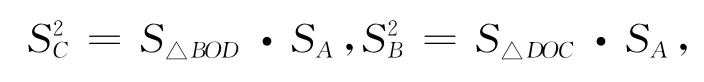
教師：非常好，這里不僅僅是內容層面的類比，更有方法層面上的類比.

3 三角形與四面體類比

教師：三角形的余弦定理是勾股定理的推廣，直角四面體的勾股定理能否推廣？能否類比三角形的余弦定理？

教師：類比三角形的余弦定理，試給出四面體余弦定理的猜想.

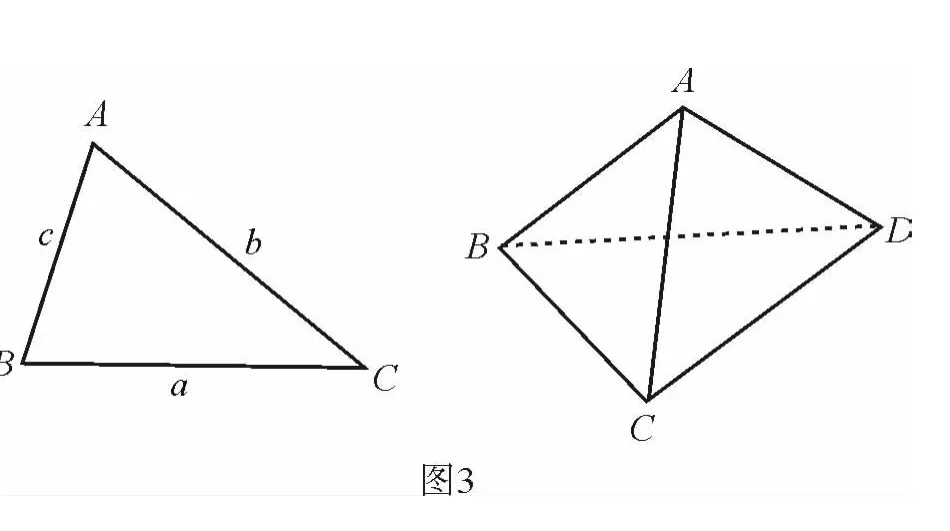
三角形的余弦定理：a2＝b2＋c2－2bccosA.

記（＊，×）表示頂點＊與×所對面在四面體內所成的角.

學生：

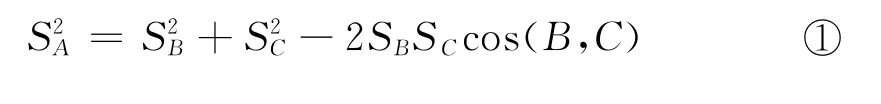
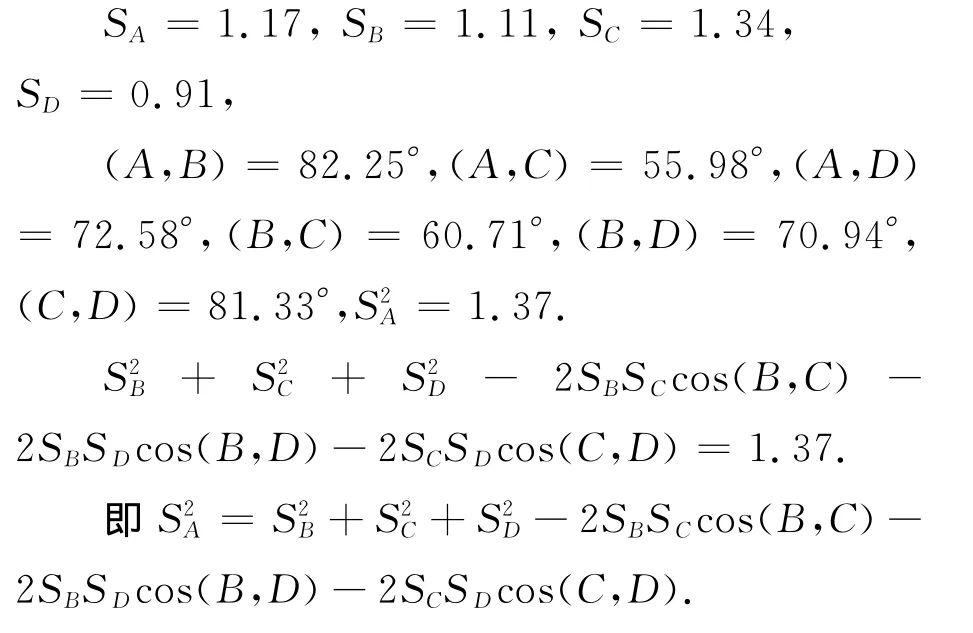
拖動點A、B、C、D改變四面體的形狀，② 式仍然成立.

教師：類似2式的式子有幾個？

學生：還有3個.（學生黑板演示）

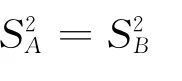
教師：（2）式如何證明？（學生暫時無法說出）

教師：能否借鑒前面直角四面體勾股定理的證法？

一學生說：和前面一樣，我們先證明三角形的余弦定理？

教師：很好，我們可以在平面中尋找靈感，然后類比到空間.那么如何證明三角形的余弦定理呢？（學生可能會利用向量來證明三角形的余弦定理，而且這種證明方法也是可以類比到空間中

教師：大家覺得這個結論正確嗎？

學生：不對，應該是：

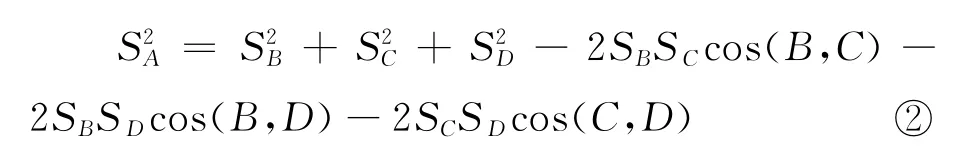
教師：為什么？

學生：可以用特殊情形檢驗，比如正四面體.

教師：嗯，這樣做是比較明智的.類比的結論是否正確我們要先進行判斷，然后進行調整，①式不正確，調整后的②式正確嗎？（大概一半的學生回答正確）

利用《幾何畫板》驗證，如圖3，測量、計算數據如下：的余弦定理，但需要用到向量的外積，留給學生課后去找資料完成.）

教師：三角形中是否有類似直角三角形的射影定理？

教師：過A作BC的垂線交BC于點D，有什么結論？（如圖4）

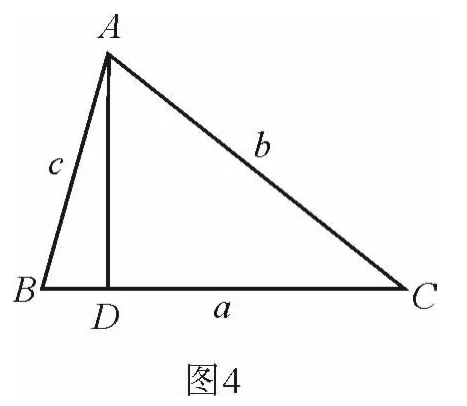
學生：a＝ccosB＋bcosC. ①

教師：很好，這就是三角形的射影定理，還有類似的式子嗎？

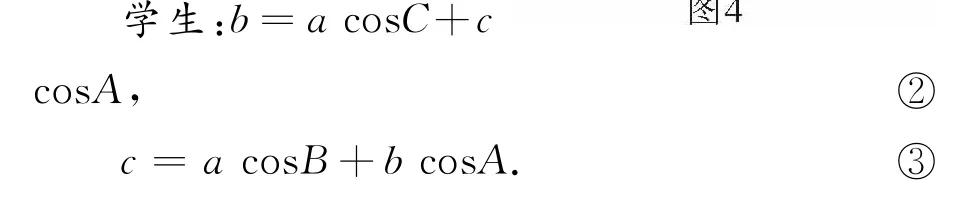
教師：由三角形的射影定理能否證得三角形的余弦定理？

學生：將②，③代入①消去cosB、cosC，得a2＝b2＋c2－2bccosA.

教師：請大家考慮一下如何證明四面體的余弦定理？（學生分組討論）

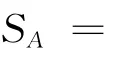
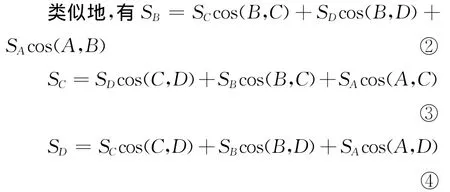
教師：不錯，這就是四面體的射影定理.

學生：將 ②，③，④ 代入 ①，消去cos（A，D），cos（A，C），cos（A，B）.即得

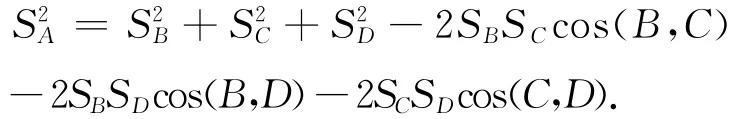
其他學生驚訝：太好了.

教師：很好，同學們我們回顧一下這節課的結構模式：

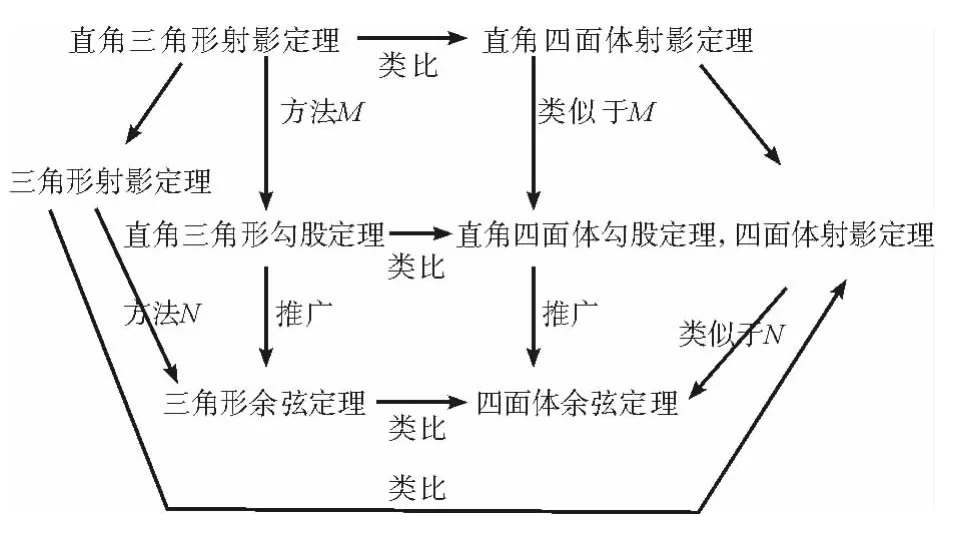
從中體會了類比方法的重要作用，類比不僅被用來發現問題，而且還能提供解決問題的思想和方法.事實上，這節課我們做了這么一件事情——將類比進行到底.

4 幾點思考

（1）學生在做類比問題的時候，總覺得沒有把握，好像是在猜謎，本質的問題是：學生對于可作類比的兩個對象之間的共性或者相似性把握不夠清楚，帶有很大的隨意性.所以教師應該引導學生關注類比對象元素是怎樣對應的，有什么合理性，這樣可以最大限度地幫助學生減少類比的盲目性.

（2）既要學會猜測，也要學會論證.在證明之前應該做適當的估計，可以借助于特殊化或者極端化的思想來檢驗.解決立體幾何問題一般來講常用的兩種思路是：一是轉化為平面幾何問題；二是尋找一個平面幾何相似的對象，通過類比獲解.這說明類比在解決立體幾何問題中的作用是不可忽視的，所以要引起高度的重視.

（3）通過直觀地觀察立體幾何，學生無法精確認識其中的數學規律，利用幾何畫板測量出各對象的數量，然后通過拖動，在動態變化中進行觀察，觀察圖形中的各種數量關系、探索圖形中的不變量，有助于學生概括數學規律和進行理性思考，豐富了學生的感性經驗.《幾何畫板》既有利于發揮學生的想象力、鼓勵學生進行數學猜想，又可以迅速、準確地反饋和檢驗學生的猜想和直覺，加強學生的反思.