平頭鋼彈侵徹鋼靶板過載特性的數值分析

盧玉斌，程永生，孫遠程

(1.中國工程物理研究院電子工程研究所，四川 綿陽 621900;2.西南科技大學制造過程測試技術教育部重點實驗室，四川 綿陽 621010)

現代戰爭要求彈丸材料的力學性能、戰斗部引信和裝藥的安定性必須滿足高過載要求。其中，引信的過載特性最重要，一方面引信強度必須能承受高過載;另一方面，為了實現彈藥在最佳炸深爆炸，引信的延時要與侵徹行程相互協調，而所有這些工作都建立在對侵徹過程中彈體過載特性的準確認識基礎上，所以對彈體侵徹過程中過載特性的研究就很重要［1-3］。

由于目標介質的多樣性和實驗條件的復雜性，使得研究硬目標侵徹過載特性存在較大困難。到目前為止，對不同介質侵徹過載的研究主要有兩種方法:① 實驗研究，隨著實驗技術的發展，可用彈內存貯技術來記錄彈丸侵徹介質時的過載曲線;②數值仿真，目前已經有一些大型商用軟件可以用來計算侵徹過程，如LS-DYNA、Autodyn、Dytran等。數值計算可使侵徹過程可視化，得到大量的時間變量，增加對侵徹機理的理解［4］。

文獻［5］指出，侵徹過載隨時間的變化規律與彈丸的著速、著角、結構參數以及靶板厚度等因素有關。本文對平頭鋼彈侵鋼靶板的過載特性進行了數值模擬，分析了彈體的長徑比、彈體著速、彈體結構響應等因素對彈丸過載特性的影響。

1 有限元計算模型

根據穿甲工程力學的理論［6］，仿真模型的建立基于如下基本假設:彈丸和靶板為均勻連續介質;整個侵徹沖擊過程為絕熱過程，不計空氣阻力，不考慮重力的作用，不考慮靶板的側邊效應，忽略靶板的整體運動;彈丸和靶板的初始應力為零。

為了說明彈體著速、長徑比及剛體假設等對侵徹過載特性的影響，本文彈體與靶板采用相同的材料，均為4043鋼，從而可以不考慮材料的影響。在有限元模擬中，采用LSDYNA有限元軟件，為了降低計算規模和節省計算時間，取1/4模型進行分析，設置非反射邊界和對稱邊界。靶板的長和寬為800 mm、厚度為10 mm，彈體直徑均為40 mm。采用Johnson-cook本構模型［7］，材料主要參數如表 1所示［8］，參考應變率取為1 s-1，參考室溫取為20℃。對于模型中材料失效參數的取值，D2～D5均取為0，然后對D1進行參數敏感性分析，通過比較由數值模擬獲得的剩余速度確定出D1=1.9。然后進行網格敏感性分析，并比較彈體的剩余速度，發現當彈體的總體網格尺寸取為2 mm，靶體長和寬劃分50份(Bias factor設置為2)、厚度劃分4份時能夠兼顧計算精度和時間。已劃分網格的有限元模型如圖1所示。

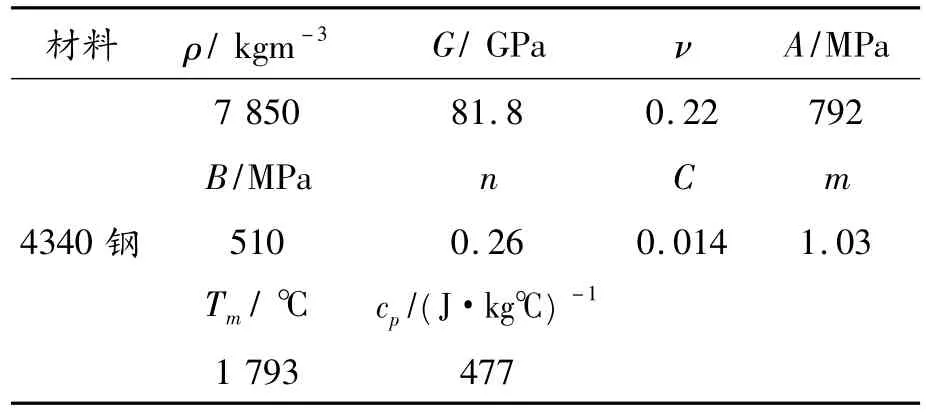
表1 材料主要參數［8］

圖1 劃分網格的有限元模型

2 數值模擬結果及分析

當彈體長度為500 mm(長徑比為12.5)、彈體速度為470 m/s時，靶板尚沒有貫穿。彈體前端、質心、后端位置處的過載時間曲線如圖2所示。由圖2可知，撞擊前端處的過載峰值極高、脈寬較窄，而質心和后端位置處的過載峰值已大大降低，且脈寬變長。從質心到后端位置的一系列節點處的過載曲線可以看出，靠近后端節點處的過載曲線較為平滑，過載峰值較低，且存在一個節點位置處的過載第一峰值最低，該節點距離后端面為48 mm。由有限元模擬結果直接得到的彈體上的剛體過載曲線如圖3所示，其過載峰值相較耦合了應力波響應的彈體質心處原始過載曲線(圖2)的峰值要低。彈體上不同位置處的應力-時間曲線如圖4所示，由圖可知，靠近彈體前端位置處的應力波以塑性應力波為主，隨著單元位置逐漸向彈體后端變化，應力波逐漸轉變為彈性應力波，且在過載峰值最低處，由于壓縮波和反射拉伸波的疊加，導致該處應力波的峰值最小，應力波曲線較為光滑。

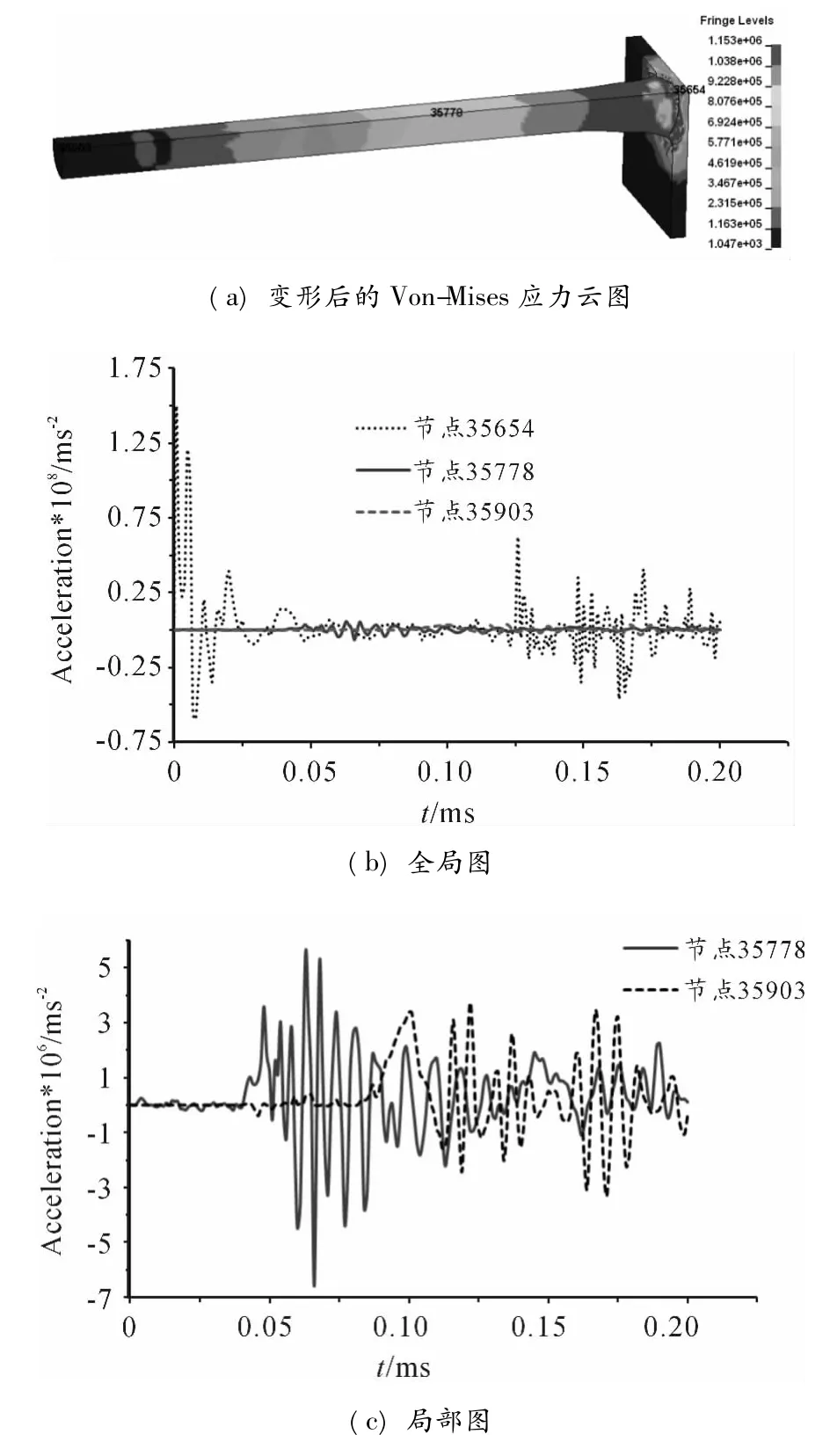
圖2 彈體前端、質心、后端的過載曲線，v=470 m/s，l/d=12.5

當彈體速度增加到800 m/s時，靶板已被完全貫穿。與彈體速度v為470 m/s時的剛體過載曲線相比，v為800 m/s時的剛體過載峰值增加，約為前者的1.7倍，與彈體速度的比值相當。由彈體上不同位置處的過載曲線結果發現當彈體速度增加時，前端和質心處的過載曲線上的峰值增加，而后端的過載曲線上的峰值降低。過載第一峰值最小的節點距離后端面為44 mm。

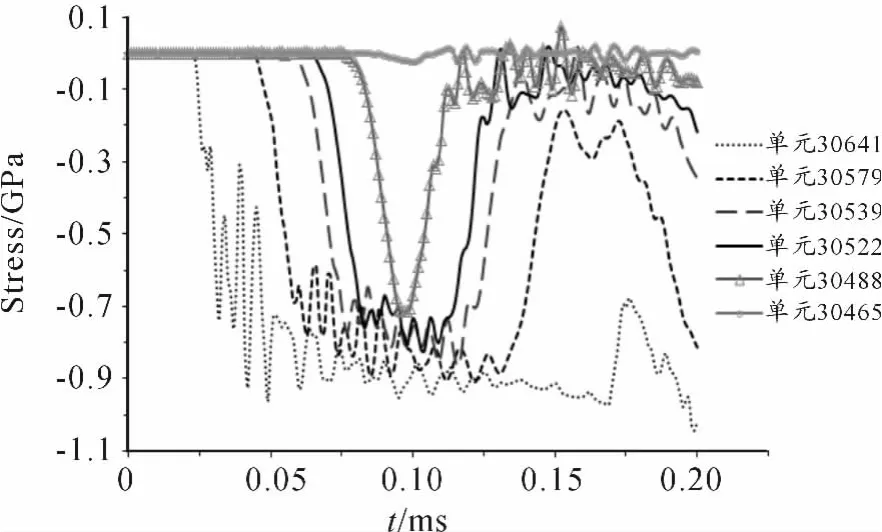
圖4 彈體上不同位置處的應力波曲線，v=470 m/s，l/d=12.5

為了進行對比，在有限元模擬中將彈體設置為剛體進行了分析。當彈體速度v=470 m/s時，彈體上不同節點處的剛體過載曲線如圖5所示。由圖5可知，其過載峰值與將彈體考慮為彈塑性變形體時的相比，約為前者(圖3)的3.43倍。并且已將靶體貫穿。

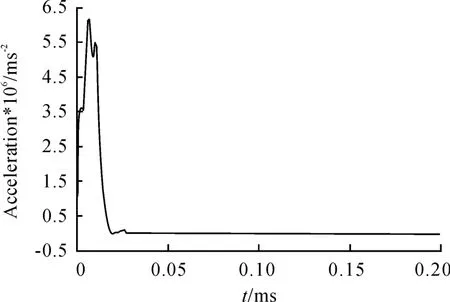
圖5 彈體為剛體時的過載曲線，v=470 m/s，l/d=12.5

當彈體的長徑比縮短為5時，不同彈體速度時彈體上的剛體過載曲線如圖6所示。彈體速度v=470 m/s和v=800 m/s與v=130 m/s時彈體速度的比值分別約為3.6倍和6.1倍，剛體過載曲線上過載峰值的比值則分別約為2.7倍和5.0倍，同時可發現剛體過載趨于0值所需的時間基本隨著彈體速度的增加而減少。與彈體長徑比為10時相比，在相同的彈體速度下(v=470 m/s、800 m/s)，剛體過載分別為前者的2.57倍和2.67倍。不同彈體速度時彈體前端、質心、后端位置處的過載時間曲線結果表明，隨著彈體速度的增加，前端的過載曲線上的峰值隨之增加，后端的過載曲線上的第一個峰值隨之降低，而質心處過載曲線上的第一個峰值先增后降。不同彈體速度時彈體上不同節點處的過載曲線結果表明，同樣存在一個靠近后端面的節點位置，該處過載的第一個峰值最小，對應于 v=130 m/s、470 m/s、800 m/s，該節點與后端面的距離分別為34 mm、4 mm、12 mm，呈現先降后增的趨勢。

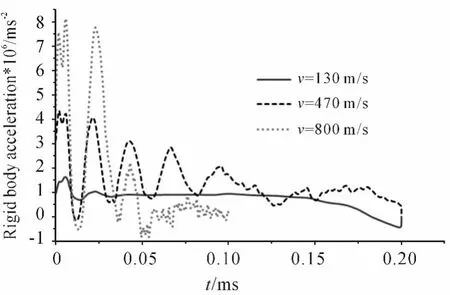
圖6 彈體上的剛體過載曲線，l/d=5

當彈體的長徑比進一步縮短為1.5時，不同彈體速度時彈體上的剛體過載曲線如圖7所示。彈體速度v=1000 m/s和v=800 m/s與v=470 m/s時彈體速度的比值分別約為2.1倍和1.7倍，剛體過載曲線上加速度峰值的比值則分別約為2.6倍和1.8倍。與彈體長徑比為5時相比，在相同的彈體速度下(v=470 m/s、800 m/s)，剛體過載分別為前者的3.3倍和3.4倍。不同彈體速度時彈體上不同節點處的過載曲線結果顯示，同樣存在一個靠近后端面的節點位置，該處過載的第一個峰值最小，對應于v=470 m/s、800 m/s、1000 m/s，該節點與后端面的距離分別為4 mm、6 mm、6 mm。

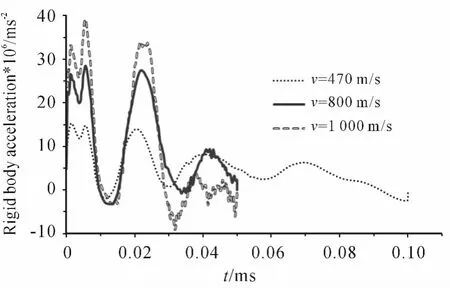
圖7 彈體上的剛體加速度曲線，l/d=1.5

不同長徑比、彈體速度以及將彈體設置為剛體時的質心和后端處過載曲線的第一峰值、以及彈體上某處過載曲線第一峰值最小時與后端面的距離總結在表2中。通過表2中的數據可得到前述關于侵徹過載的變化規律。

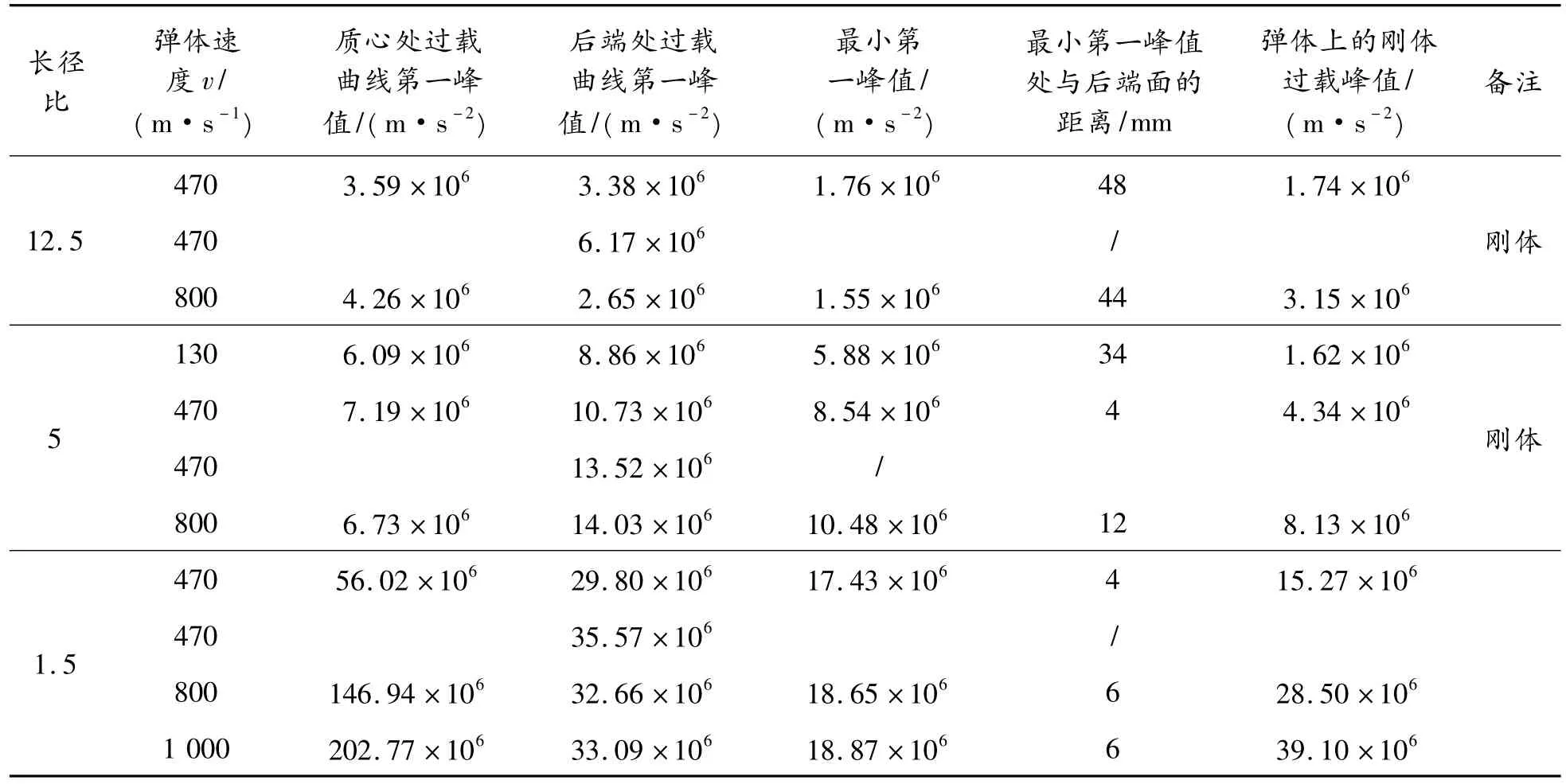
表2 不同條件時過載峰值總結

3 結論

通過對具有不同的著靶速度和長徑比的鋼質平頭彈體侵徹鋼靶板的仿真，分析了彈體過載的變化情況，得到如下結論:

(1)靠近彈體后端節點處的過載曲線較為平滑，過載峰值較低，且存在一個節點位置處的過載第一峰值最低，該節點與后端面的距離和彈體的長徑比及彈體的入靶速度均有關系，變化范圍為4～48 mm。

(2)靠近彈體前端位置處的應力波以塑性應力波為主，隨著單元位置逐漸向彈體后端變化，應力波逐漸轉變為彈性應力波，且在過載峰值最低處，由于壓縮波和反射拉伸波的疊加，導致該處應力波的峰值最小，應力波曲線較為光滑。

(3)由有限元模擬結果直接得到的彈體上的剛體過載曲線的過載峰值相較彈體質心處的原始過載曲線的峰值要低，說明原始過載曲線中耦合了應力波響應的影響。

(4)彈體長徑比相同時，隨著彈體入靶速度的增加，彈體上的剛體過載曲線的過載峰值隨之增加，侵徹深度同樣增加;當彈體入靶速度相同時，隨著彈體長徑比的減小，彈體上的剛體過載曲線的過載峰值隨之增加，侵徹深度隨之降低。

(5)把彈體設置為剛體得到的過載曲線的過載峰值與將彈體考慮為彈塑性變形體時彈體上的剛體過載曲線的加速度峰值相比，約為后者的好幾倍，前者的侵徹深度也較大。

［1］劉璞，施坤林，黃惠東.鋼板侵徹過載的三維數值模擬［J］.探測與控制學報，2006，28(1)：25-28.

［2］劉立軍，祖靜，范錦彪，等.動能子彈侵徹鋼板加速度測試與分析［J］.傳感器與微系統，2010，29(6)：15-17.

［3］Zhang W，Cheng L J，Xiong J J，et al.Ultra-high g deceleration-time measurement for the penetration into steel target［J］.International Journal of Impact Engineering，2007，34(3)：436-447.

［4］劉偉釗，陳侃，李蓉，等.不同介質侵徹過載特征參量有限元仿真方法［J］.科學技術與工程，2011，11(5)：3494-3497，3500.

［5］屈新芬，商順昌，楊晴.影響彈丸侵徹性能的因素分析及引信方案探討［J］.信息與電子工程，2003，1(3)：51-55.

［6］趙國志.穿甲工程力學［M］.北京：兵器工業出版社，1992：106-107.

［7］LivermoresoftwareTechnologyCorporation. LS-DYNA Keyword User’s Manual(970v)［Z］.Livermore，2003.

［8］張清爽.彈丸侵徹裝甲鋼板過載特性數值模擬［J］.彈箭與制導學報，2009，29(4)：133-135.

［9］張迪.擴展有限元法在彈靶侵徹中的應用［J］.重慶理工大學學報：自然科學版，2012(5)：43-46.