基于模式搜索算法的結構被動控制系統參數優化研究

徐慶陽，李愛群，丁幼亮，胡燦陽

(1.南京審計學院國際審計學院 江蘇公共工程審計重點實驗室，南京 211815;2.東南大學 土木工程學院，東南大學混凝土與預應力混凝土結構教育部重點實驗室，南京 210096)

設置被動控制系統的結構減震設計關鍵，在于合理地確定阻尼器的位置與參數［1］。較早的結構減震研究主要關注減震裝置在結構中的可行性，并通過大量算例來對比不同參數或布置下減震效果的差異［2-3］，直接將優化方法應用于減震控制的研究還較少［4］，并且在進行減震結構優化分析時均要對結構進行簡化［5］，影響了優化方法在復雜工程中的應用。

1 結構減震裝置參數優化的數學模型

結構減震系統的優化需要確定設計變量、目標函數與約束條件來建立數學模型［6］。減震結構優化是期望在合理的減震成本基礎上將地震作用下的結構響應降低到某一限值以下，其數學模型可以通過下式來表達:

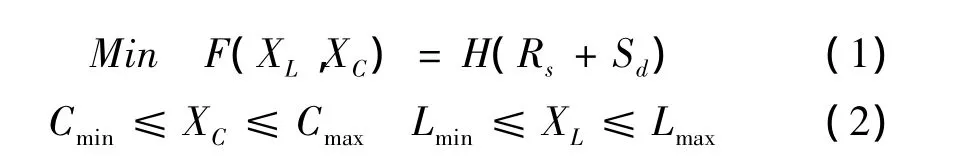
式中:XL為減震裝置位置變量，XC為減震裝置參數變量，Rs為減震結構地震響應，Sd為減震裝置的數量表達式。減震結構被動控制系統參數優化模型的目標函數無法表達為設計變量的具體函數形式，更無法求得其關于設計變量的導數或梯度函數。這就要求優化算法在搜索過程中不依靠目標函數的梯度、能在搜索過程中自動獲取和積累有關搜索空間的知識，并能自適應地控制搜索過程。

減震參數優化問題中設計變量取值空間往往是連續的，尋優的過程為沿著可行解的取值范圍進行搜索。僅僅利用目標函數值的信息直接建立搜索求解的方法稱為直接搜索法(direct search method)。以往研究結果表明［7-8］，結構減震效果與減震裝置主要參數的關系曲線往往為一單峰凹凸曲線，不依賴求導的搜索方法將在結構減震參數優化分析中具有較好的適用性［9］。

2 模式搜索算法原理及其實現

2.1 模式搜索算法理論基礎

模式搜索算法解無約束優化問題的需要確定一個可供選擇的搜索方向模式和一個試探性移動的準則。這個模式的一般表示式為矩陣［10］:

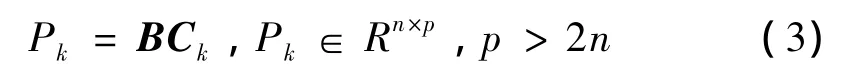
其中:B∈Rn×n稱為基矩陣，在每一步迭代中是不變的。C∈Zn×p，稱為生成矩陣，并記為:

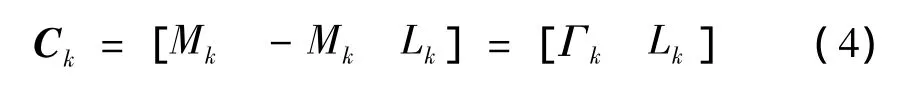
Mk∈M?Zn×n，M是由整數元構成的n階非奇異方陣的集合，Lk∈Zn×(p-2n)，至少包含一零向量列。模式搜索法的搜索方向一般取Pk的某一列，Ck包含零向量表明迭代中會出現不能移動的情況。

模式確定后，考慮進行試探性移動。對于步長Δk∈R，Δk＞0，定義試探步:

① sk∈ΔkPk≡Δk［BΓk，BLk］;② 若 min{f(xk+y)，y∈ΔkBΓk}＜f(xk)，則 f(xk+sk)＜f(xk)，這時記sk=sk’且 xk+1=xk+sk。sk是模式 Pk的某一列乘以步長Δk的得到的。條件②表明，只要前2n個方向中的某一個方向能使目標函數值得到下降，那么，sk也應該能使函數值得到下降。

2.2 基本模式搜索算法

當目標函數f(x1，x2，…，xn)無法用具體解析表達式來描述時，采用模式搜索法求解目標函數極值問題的計算步驟為［11］:

(1)任選初始近似點B1，以它為初始基點進行探索;

(2)為每一獨立變量xi(i=1，2，…，n)選定步長為=［0，…，0，δi，0，…，0］。式中，Δi是第 i個分量為δi，而其他所有分量均為零的向量;

(3)計算出初始基點B1的目標函數值f(B1)，若點B1+Δ1的目標函數值f(B1+Δ1)＜ f(B1)，就以B1+Δ1為臨時矢點，并記為T11。若B1+Δ1不比B1點準，就試驗B1-Δ1，如果它比B1點準，就以它為臨時矢點。否則，仍以B1為臨時矢點。即:

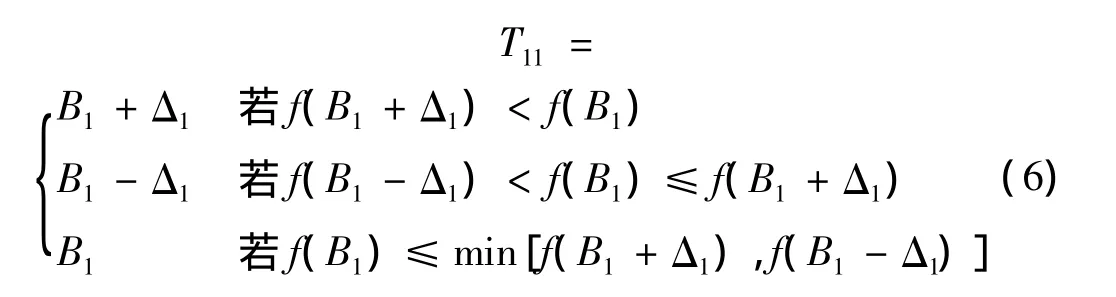
對于下一個獨立變量x2進行類似的攝動。這時，用臨時矢點T11代替原來的基點B1。N個變量都攝動之后，得到臨時矢點T1n，并令 T1n=B2，原來的基點B1和新基點B2確定了第一個模矢。

(4)將第一個模矢延長一倍，得到第二個模矢的初始矢點T20，T20=B1+2(B2-B1)=2B2-B1;

(5)在T20附近進行如上的探索，建立臨時矢點T21，T22，…，T2n，以 T2n為第三個基點 B3。這樣，B2、B3就確立了第二個模矢。第三個模矢初始矢點為T30，T30=B2+2(B3– B2)=2B3– B2;

(6)繼續上述過程，對于第i個模矢，如果f(Ti0)＜f(Bi)，但沿各坐標方向的所有攝動均得不出比Ti0更好的點，則不把這個模矢延長。若f(Ti0)＜f(Bi)，且由Ti0產生不出比Bi更好的點，則退回到Bi，并在Bi附近進行探索。如果能得出新的下降點，即可引出新的模矢;否則，將步長縮小，以進行更精細的探查。當步長縮小到要求的精度時，即可停止迭代，確定已找到最優點。

2.3 約束問題的模式搜索算法

大部分優化問題均存在約束條件，包括等式約束和不等式約束。其形式如下:

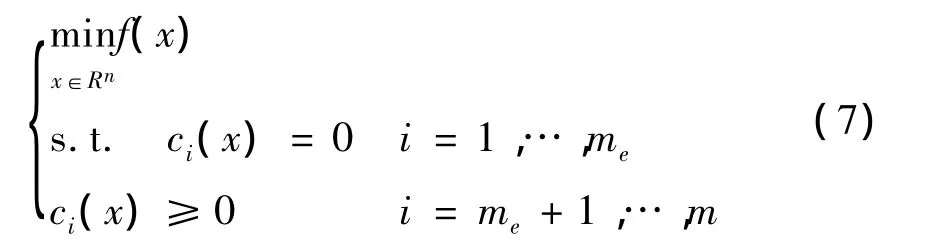
解決此類優化問題的常用方法是罰函數法，利用目標函數f(x)和約束函數c(x)所構成的具有“罰性質”的函數［12］:

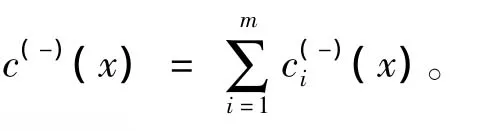
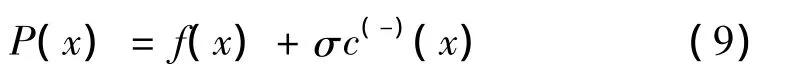
其中:σ＞0為常數，稱為罰因子。

本文主要針對簡單罰函數和乘子罰函數，結合前面的模式搜索算法，給出簡單罰函數模式搜索算法和乘子罰函數算法。

3 模式搜索算法在減震優化中的實現

減震參數優化分析包含兩個部分的內容:結構地震響應分析與模式搜索算法尋優。這里通過Matlab編制目標函數程序，實現模式搜索優化程序對減震結構有限元分析結果的調用，從而實現優化程序與有限元程序的互動，流程圖1所示。

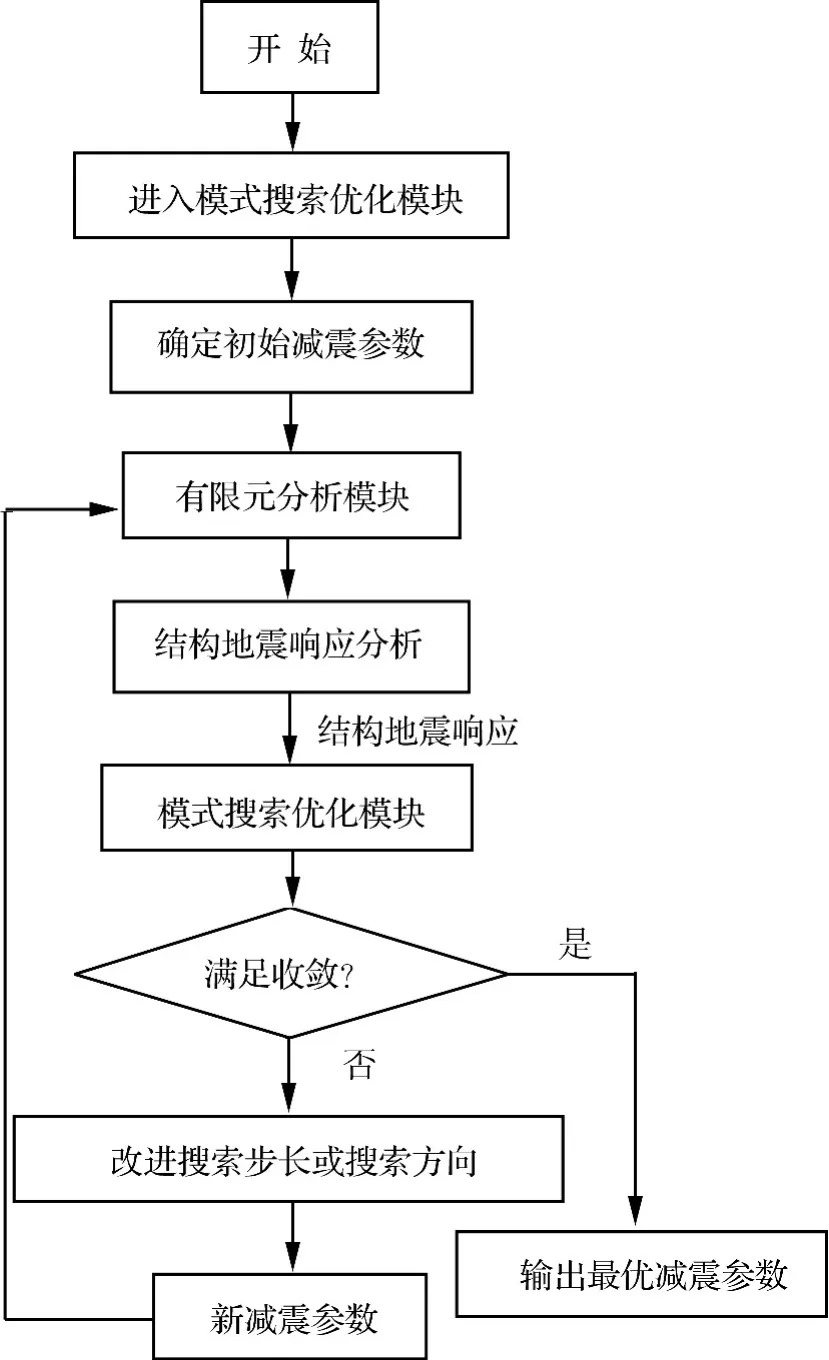
圖1 結構減震優化的模式搜索算法流程圖Fig1 Pattern search algorithm flowchart for seismic parameter optimization of reduction structure

3.1 多峰值多元函數最小化分析

為驗證模式搜索算法在多峰值模型尋優過程中是否能有效準確地找到全局最優解，首先選取一典型多峰值函數Shubert函數，用來驗證本文程序在多參數尋優分析中的有效性。

圖2為該函數的三維示意圖，具有兩個獨立變量x、y的Shubert函數定義如式(10)所示。該函數存在多個局部最小值，但僅存在唯一全局最小值。這里采用本文的優化程序來進行Shubert函數全局最優解的尋優，尋優過程與結果如圖3所示。

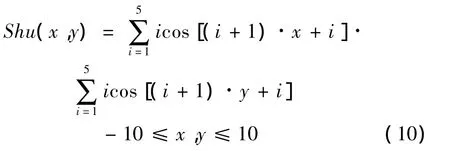
圖中左上為優化過程中目標函數值的變化過程，右上為優化過程中相對步長值的變化過程，左下為每一步尋優計算目標函數的次數，右下為最終得出的最優目標函數值。初始起點選擇為［-1，-1］，尋優步數共計56步，最終因搜索相對步長小于設定限制而達到收斂。最優函數值為-186.730 9，對應自變量取值為［4.858 06，-0.800 32］。

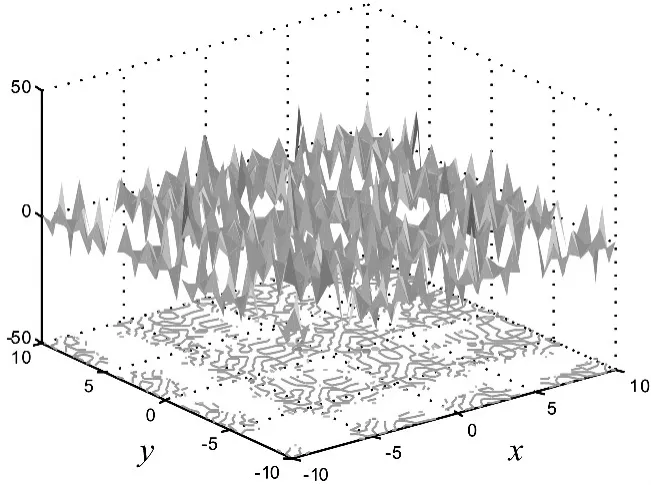
圖2 Shubert函數三維圖形Fig.2 Three-dimensional graphic of Shubert function

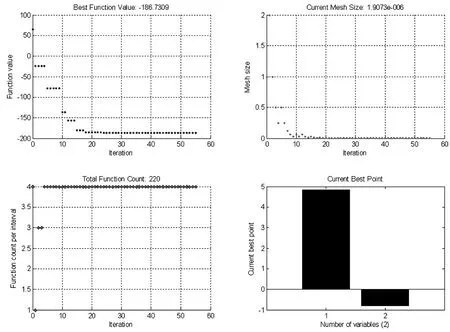
圖3 Shubert函數采用模式搜索算法優化過程Fig.3 Optimization process of Shubert function by using pattern search algorithm

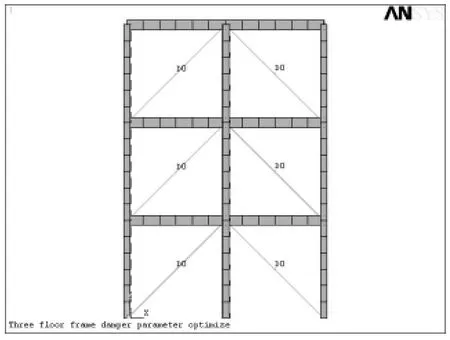
圖4 平面框架有限元模型Fig.4 Finite element model of plane frame

結果顯示，采用模式搜索算法可以有效準確地求得多峰多元問題的全局最優解。

3.2 三層雙跨平面框架減震參數優化分析

為進一步驗證算法在結構減震參數優化分析中的可行性，選用一雙跨三層混凝土框架進行分析。結構有限元模型如圖4所示。框架柱截面面積0.16 m2，梁截面面積0.18 m2，粘滯流體阻尼器沿對角線布置。

設計變量為阻尼器的阻尼系數，目標函數為結構基底剪力，優化程序將尋找使結構基底剪力達到最小值所對應的阻尼系數。

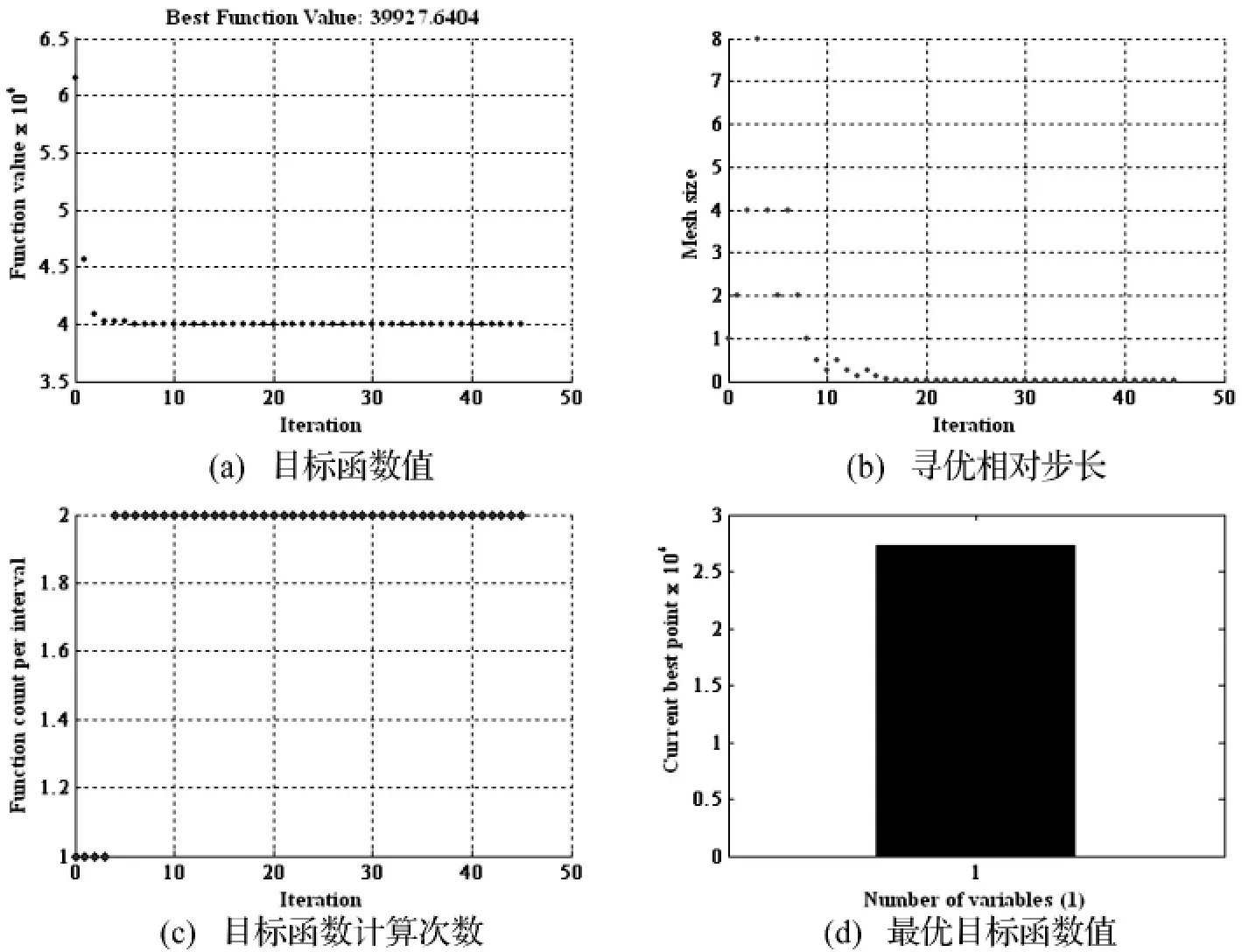
圖5 框架模型減震參數優化過程Fig.5 Damper parameter optimization process of one frame through pattern search algorithm

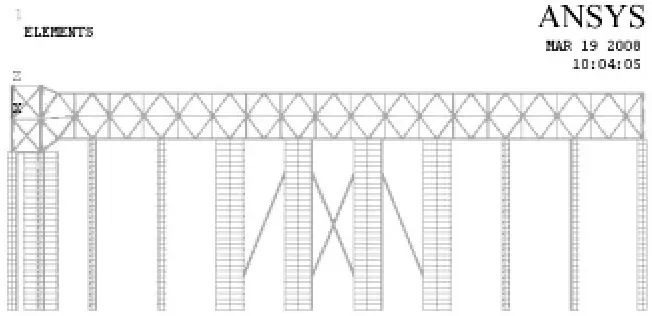
圖6 平面排架有限元分析模型Fig.6 Finite element model of plane frame

初始阻尼系數定為50 000 N·s/m。圖6為模型采用線性粘滯流體阻尼器減震參數優化的過程與優化結果，其中(a)為優化過程中目標函數值的變化過程，(b)為優化過程中相對步長值的變化過程，(c)為每一步尋優計算目標函數的次數，(d)為最終得出的最優目標函數值。結果顯示最優阻尼系數為2 733 790 N·s/m，對應的結構基底剪力為39 928 N，未減震結構基底剪力為98 792 N，最優減震幅度達到59.58%。尋優步數共計46步，最后尋優步長小于設定值因而收斂。在第6步時目標函數已基本接近最優值。

4 平面排架減震參數優化分析

這里選取某單榀排架來進一步驗證優化算法在減震參數優化分析中的可靠性與穩定性。該平面排架為某大跨機庫結構中的一榀，上部為鋼結構桁架，下部為鋼筋混凝土支撐住，柱間設有斜撐。模型在支撐柱與上部鋼結構節點之間設置粘滯流體阻尼器。鋼結構桿件采用Link1單元，下部支撐柱采用Beam3單元，消能支撐采用Combin4單元來模擬。結構Ansys有限元模型如圖6所示。

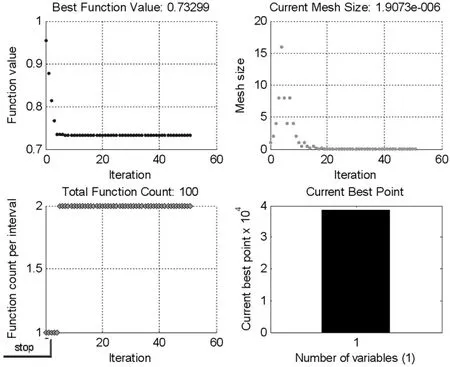
圖8 Gengma波作用下消能支撐減震參數優化結果Fig.8 Damper parameter optimization process under Gengma seismic wave

在El-Centro與Gengma兩條不同地震波作用下，優化模型以結構基底剪力的減震效果為目標函數，消能支撐參數優化分析結果如圖7～8所示。

最優阻尼系數為38 849 kN·s/m，對應基底剪力減震幅度為47.96%，優化算法經過48步達到收斂，在第7步達到最優值。

最優阻尼系數為38 688 kN·s/m，對應基底剪力減震幅度26.71%，優化算法經過52步達到收斂，在第8步達到最優值。

上面的算例表明，地震波類別對阻尼器參數優化結果影響較小。優化算法達到收斂的尋優步數一般在50左右，但往往在10步左右即可達到或接近最優解，而后面的迭代對于最優解的改進僅僅是針對小數點后若干位的，因此該優化算法其實可以在很少的步數內尋找到最優解，具有較高的效率。

5 結論

本文選取模式搜索算法作為結構減震系統參數優化分析算法，在研究模式搜索算法的基本原理與實現技術基礎上，編制了結構減震參數優化程序，通過多峰多元函數以及單榀框架模型對優化程序進行有效性與準確性驗證，并通過一單榀排架驗證了不同地震波下優化程序的穩定性。結果表明，不依賴目標函數導數的搜索方法將在結構減震參數優化分析中具有較好的適用性，尋優過程迅速。由于在求目標函數時利調用了有限元分析結果，而優化過程利用Matlab本身優化工具箱，因此本文方法結果具有較高的可信度與可行性。

［1］周福霖.工程結構減震控制［M］.北京:地震出版社，1997:66-78.

［2］李 濤，張洵安.巨子型有控結構體系中黏滯阻尼器參數研究［J］.地震工程與工程振動，2011，31(4):71-76.

LI Tao，ZHANG Xun’an.Research on parameters of viscous dampers inserted in MSCSS［J］.Journal of Earthquake Engineering and Engineering vibration.2011，31(4):71-76.

［3］王立偉，蔡新江，田石柱.黏滯阻尼器耗能減振工程應用設計方法研究［J］.地震工程與工程振動，2011，27(5):161-167.

WANG Li-wei，CHAI Xin-jiang，TIAN Shi-zhu.Research on practical design method using liquid viscous damper passive energy dissipation in building［J］.Journal of Earthquake Engineering and Engineering vibration. 2011，27(5):161-167.

［4］吳澤厚，周福霖.消能減震建筑結構的計算分析［J］.重慶建筑大學學報，2002，24(2):47-51.

WU Ze-hou，ZHOU Fu-lin.Optimization of energy dissipation braces in frame structures［J］.Journal of Chongqing Jianzhu University，2002，24(2):47-51.

［5］周星德，彭宣茂.基于遺傳算法的建筑結構最優阻尼研究［J］.計算力學學報，2005，22(6):780-784.

ZHOU Xing-de，PENG Xuan-mao.Study on optimal damper of building structures using real coded genetic algorithms［J］.Chinese Journal of Computational Mechanic，2005，22(6):780-784.

［6］薛 毅.最優化原理與方法［M］.北京:北京工業大學出版社，2008:125-133.

［7］徐慶陽.大跨空間網架結構減震技術研究與應用［D］.南京:東南大學，2005.

［8］黃銘楓，唐家祥.高層建筑粘彈性阻尼器的優化設置［J］.華中科技大學學報，2001，29(11):73-75.

HUANG Min-feng，TANG Jia-xiang.Optimum installation of the viscoelastic dampers for the tower structure［J］.J.Huazhong Univ.of Sci.＆ Tec.，2001，29(11):73-75.

［9］國 巍，李宏男.考慮扭轉耦聯效應的附屬結構最優位置分析［J］.計算力學學報，2009，26(6):797-803.

GUO Wei，LI Hong-nan.Secondary system’s optimal position analysis concerning the lateral-torsion coupling effect［J］.Chinese Journal of Computational Mechanic，2009，26(6):797-803.

［10］Lewis R M，Torczon V.A globally convergent augmen-ted Lagrangian pattern search algorithm for optimization with general constraints and simple bounds［J］.SIAM Journal on Optimization，2002，12(4):1075-1089.

［11］Yosef S S，Bruce A B.Optimization by pattern search［J］.European Journal of Operational Research，1994，78(13):388-303.

［12］雷英杰，張善文，李繼武，等.MATLAB遺傳算法工具箱及應用［M］.西安:西安電子科技大學出版社，2004:146-207.