砂土液化大變形本構(gòu)模型的三維化及其數(shù)值實(shí)現(xiàn)①

王 睿，張建民，王 剛

（1．清華大學(xué)水沙科學(xué)與水利水電工程國家重點(diǎn)實(shí)驗(yàn)室，北京 100084；2．清華大學(xué)土木水利學(xué)院，北京 100084；3．二灘水電開發(fā)有限責(zé)任公司，四川 成都 610021）

0 引言

砂土的液化后大變形作為地震液化誘發(fā)災(zāi)害的重要成因，自幾次強(qiáng)震以來［1－2］一直是巖土工程抗震方面的一個研究熱點(diǎn)。針對砂土在循環(huán)加載條件下的動力響應(yīng)，很多學(xué)者進(jìn)行了卓有成效的研究，并提出了一系列 包 括 邊 界 面 模 型［3－5］、多 面 模 型［6－7］和 廣義塑性模型［8］等砂土循環(huán)本構(gòu)模型。但是這些模型中，鮮有能夠基于砂土液化后大變形的機(jī)理有效模擬砂土液化后大變形的產(chǎn)生與累積。

基于試驗(yàn)觀察，Shamoto和張建民［9］以及張建民和王剛［10－11］提出了飽和砂土液化后大變形的機(jī)理解釋。將體變分解為有效球應(yīng)力變化引起的體變、可逆性剪切體變和不可逆性剪切體變，揭示了不排水循環(huán)加載條件下砂土液化后剪應(yīng)變的發(fā)展和累積與三個體積應(yīng)變分量之間的內(nèi)在聯(lián)系。根據(jù)體積相容性條件，定量的描述了砂土液化后在零有效應(yīng)力條件下所產(chǎn)生的“似流體”剪應(yīng)變 （fluid－like shear strain）γ0。

以此機(jī)理為基礎(chǔ)，王剛和張建民［12］在邊界面塑性理論［13］框架下，建立了一個可以描述飽和砂土液化后大變形的彈塑性循環(huán)本構(gòu)模型。該模型根據(jù)試驗(yàn)規(guī)律定義了區(qū)別于其他已有模型的可逆和不可逆剪脹速率，從而實(shí)現(xiàn)了對砂土循環(huán)剪切體變的正確描述。通過體積相容性條件，有效地計(jì)算砂土液化后剪切變形的產(chǎn)生與累積，為定量描述砂土液化后大變形提供了一個科學(xué)的建模方法。由于三維條件下可逆性剪脹面上的應(yīng)力映射規(guī)則并未給定，以及根據(jù)邊界面上映射規(guī)則確定的流動方向數(shù)值上求解成本過大，該模型可以在二維應(yīng)力空間中應(yīng)用，但無法用于真正的三維計(jì)算。

基于該模型，本文提出了與其相適應(yīng)的三維應(yīng)力空間中邊界面和剪脹面上的應(yīng)力映射規(guī)則，并根據(jù)數(shù)值計(jì)算能力需求，調(diào)整了塑性流動方向，對砂土液化大變形本構(gòu)模型進(jìn)行了三維化。利用高效的數(shù)值算法，在OpenSees［14］開源有限元平臺上對模型進(jìn)行三維的數(shù)值實(shí)現(xiàn)；通過對試驗(yàn)的模擬和三維地基動力反應(yīng)分析，驗(yàn)證模型和數(shù)值算法的有效性。

1 模型的三維形式

由于王剛和張建民［11－12］對本模型大部分要素做了詳細(xì)的描述，本文重點(diǎn)討論在三維應(yīng)力空間中模型的相關(guān)映射規(guī)則，其他方面僅簡要介紹。

本文各處張量均采用加黑斜體，標(biāo)量采用斜體表示。除特別聲明變量外，變量大多采用土力學(xué)常規(guī)符號表達(dá)。

1．1 基本應(yīng)力應(yīng)變關(guān)系

模型采用彈塑性應(yīng)力應(yīng)變關(guān)系

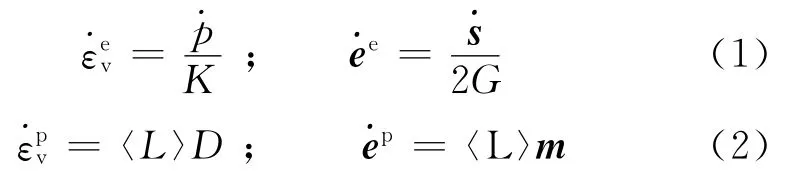
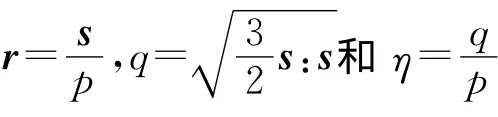
1．2 彈性模量

彈性模量采用Richart［15］建議的方式定義

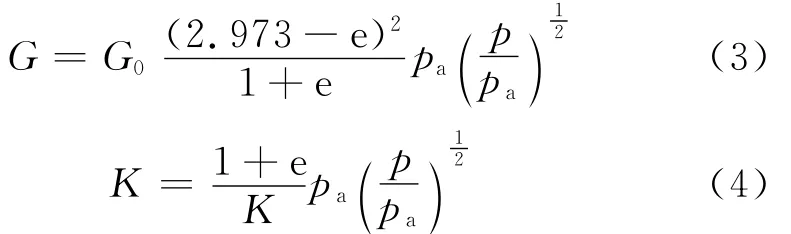
pa為標(biāo)準(zhǔn)大氣壓。

1．3 破壞面、邊界面和可逆性剪脹面

由于本模型為邊界面塑性理論［13］?框架下的本構(gòu)模型，在確定各種映射規(guī)則前，首先需要確定本模型所使用的破壞面、邊界面和可逆性剪脹面，分別定義如下：

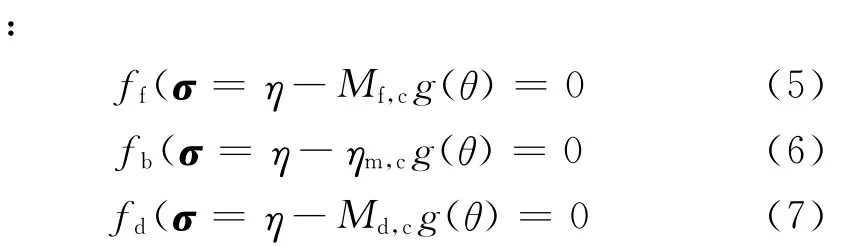
式中Mf，c為三軸壓縮條件下的破壞應(yīng)力比；ηm，c為歷史最大三軸壓縮應(yīng)力比；Md，c為三軸壓縮條件下可逆性剪脹的產(chǎn)生與釋放的分界；θ為應(yīng)力羅德角；而形狀函數(shù)g（θ）則為根據(jù)張建民［16］的簡化函數(shù)（圖1）。

1．4 加載與反向加載判斷

模型通過塑性加載指數(shù)符號判定加載與反向加載：

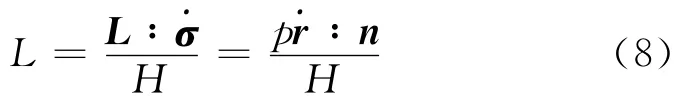
1．5 邊界面上的映射規(guī)則與塑性模量

在邊界面塑性理論框架下［13］，塑性模量受到當(dāng)前應(yīng)力點(diǎn)到其在邊界面上投影的距離控制，因此需要定義恰當(dāng)?shù)挠成湟?guī)則。

對于當(dāng)前應(yīng)力在邊界面上的投影ˉr，借鑒王志良等［3］提出的相應(yīng)映射規(guī)則，定義為上一次反向加載點(diǎn)（應(yīng)力反轉(zhuǎn)點(diǎn)）ain到當(dāng)前應(yīng)力點(diǎn)r連線的延長線與邊界面的交點(diǎn)（圖1）。因此可以將邊界面上投影點(diǎn)表示為

其中β可以通過將式（9）帶入式（6）求解。

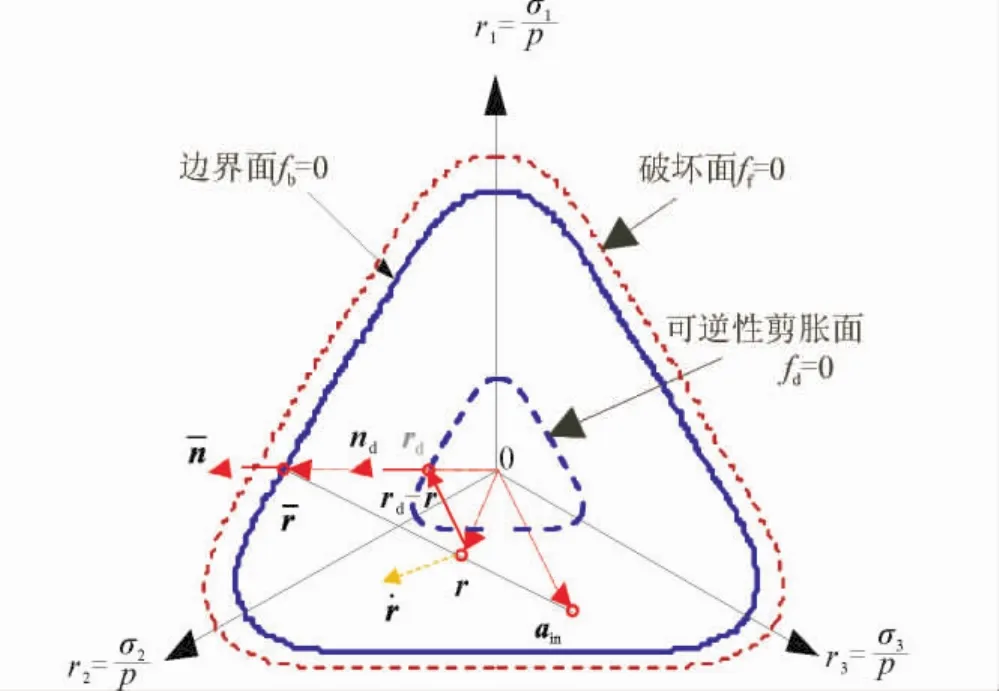
圖1 模型映射規(guī)則Fig．1 Mapping rules for the model．

假定偏應(yīng)力空間中的加載方向n與偏應(yīng)變增量方向m一致，并定義為沿ˉr方向的單位張量：

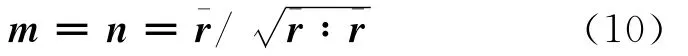
實(shí)際上，嚴(yán)格根據(jù)彈塑性理論n應(yīng)當(dāng)為邊界面在應(yīng)力投影點(diǎn)處的單位外法向，但是由于在模型數(shù)值化時(shí)，對于邊界面函數(shù)求解外法向在數(shù)值上十分困難且計(jì)算成本很高，因此在模型的三維化中采用這一調(diào)整后的加載與流動方向。

在定義了模型在邊界面上的應(yīng)力投影規(guī)則后，塑性模量的確定可以通過下式得到：

1．6 可逆剪脹面上的映射規(guī)則和可逆剪脹速率

由于王剛和張建民［12］并未定義三維空間中可逆剪脹面上的應(yīng)力投影規(guī)則，若采用模型二維形式中可逆性剪脹生成與釋放的判別標(biāo)準(zhǔn)和剪脹速率，將在三維空間中出現(xiàn)誤差。以圖1中的應(yīng)力狀態(tài)為例，按照模型二維形式中的判斷規(guī)則，由于｜η｜≥Md，cg（θ）且｜η｜＞0，因此判斷為發(fā)生可逆性剪脹，可逆性剪脹速率Dre＜0。而實(shí)際上對于三維應(yīng)力空間，可逆性剪脹／減縮的判斷應(yīng)當(dāng)由當(dāng)前應(yīng)力點(diǎn)r在應(yīng)力反轉(zhuǎn)點(diǎn)ain到r的方向上與可逆性剪脹面的相對位置確定。由此，定義當(dāng)前應(yīng)力點(diǎn)r在可逆性剪脹面上的投影rd為（圖1）：

在該映射規(guī)則下，可以定義三維應(yīng)力空間中可逆性剪脹的產(chǎn)生與釋放判定標(biāo)準(zhǔn)為

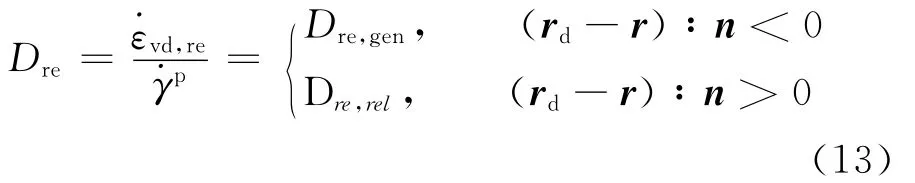
式中，Dre，gen為可逆性剪脹產(chǎn)生速率；Dre，rel為釋放速率。

相應(yīng)的，三維條件下可逆性剪脹產(chǎn)生速率為

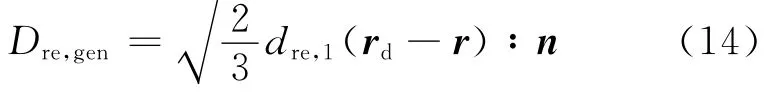
可逆性剪脹釋放速率仍為［12］

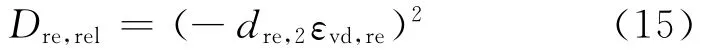
dre，2為可逆性剪脹釋放參數(shù)。

根據(jù)新的映射規(guī)則和可逆性剪脹的產(chǎn)生與釋放判定標(biāo)準(zhǔn)，圖1所示情況發(fā)生可逆性剪縮，可逆性剪脹速率Dre＝Dre，rel＞0，這是由于當(dāng)前應(yīng)力點(diǎn)處于其所對應(yīng)的邊界面上投影點(diǎn)“以內(nèi)”。

1．7 不可逆剪脹速率

不可逆剪脹速率仍參照王剛和張建民［12］：

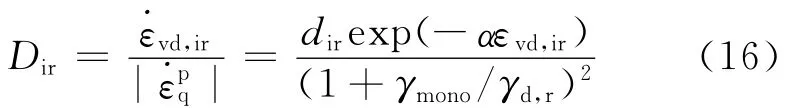
dir，α和γd，r為不可逆性剪脹參數(shù)；γmono為單向剪應(yīng)變長度。

1．8 液化后大變形

通過將式（4）帶入式（1）積分，可以得球應(yīng)力發(fā)展至零時(shí)的εvc閾值，即εvc，0：

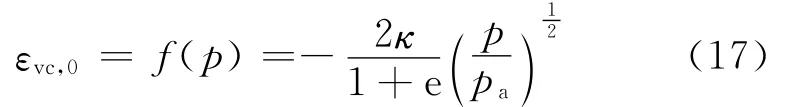
當(dāng)εvc大于εvc，0時(shí)，有效球應(yīng)力保持為零，土體進(jìn)入液化狀態(tài)，式（1）中的體變公式不再有效。εvc轉(zhuǎn)而由體積相容性確定：

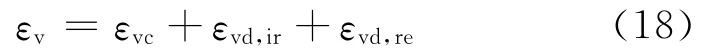
此時(shí)各剪脹關(guān)系依然有效，因此只有當(dāng)足夠的剪應(yīng)變ep發(fā)生時(shí)（即液化后大變形），才能產(chǎn)生充分的εvd，re，使得土體離開液化狀態(tài)［10－11］。

2 模型數(shù)值實(shí)現(xiàn)

通過高效數(shù)值算法，在OpenSees［14］中進(jìn)行了三維化模型的數(shù)值實(shí)現(xiàn)。

2．1 零有效應(yīng)力處理方法

關(guān)于零有效應(yīng)力狀態(tài)下模型的數(shù)值處理，采用王剛和張建民［12］提出的方法，即設(shè)定一最小有效球應(yīng)力pmin，使得

此時(shí)，εvc，0可表示為

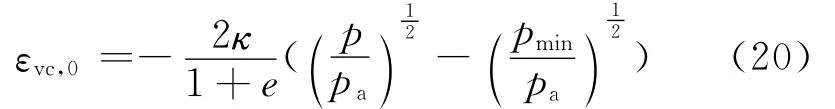
2．2 應(yīng)力積分算法

采用分子步的Cutting Plane半顯式積分算法進(jìn)行應(yīng)力積分。對于半顯式積分算法，需要控制每一步應(yīng)力積分時(shí)的應(yīng)變步長，否則可能出現(xiàn)不收斂的情況。為了增加算法穩(wěn)定性，將有限元得到的應(yīng)變增量分成子步后再進(jìn)行應(yīng)力積分計(jì)算。

計(jì)算子步長時(shí)，首先對下一步應(yīng)力進(jìn)行彈性預(yù)測，當(dāng)剪應(yīng)變增量或剪應(yīng)力比增量超過容許值，則將步長拆分為n個子步：

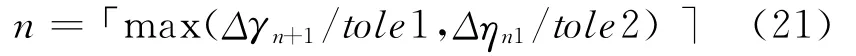
對于每一個子步采用Cutting Plane算法進(jìn)行應(yīng)力積分。該算法首先由Simo和Ortiz［17］提出，主要思路是在彈性預(yù)測應(yīng)力增量的基礎(chǔ)上，通過對一致性條件φ＝0中函數(shù)φ的一階展開逼近一致性條件進(jìn)行塑性修正，最后得到實(shí)際應(yīng)力增量，步驟如下：

（1）初始化局部迭代次數(shù)、塑性應(yīng)變和塑性加載指數(shù)：

（2）彈性預(yù)測：

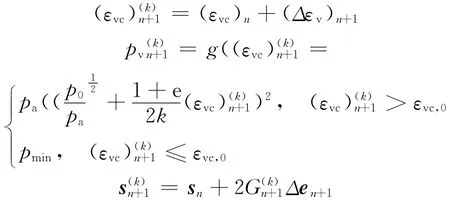
（3）檢查一致性條件，判斷加載／反向加載：

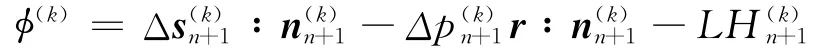
當(dāng)φ（k）＞0，發(fā)生塑性加載，進(jìn)行第4步；當(dāng)φ（k）＜0，應(yīng)力反轉(zhuǎn)，更新應(yīng)力反轉(zhuǎn)點(diǎn)（ain）n＋1＝rn，進(jìn)行第6步。

（4）通過計(jì)算塑性加載指數(shù)增量進(jìn)行塑性修正：

更新塑性加載指數(shù)和應(yīng)力應(yīng)變狀態(tài)：

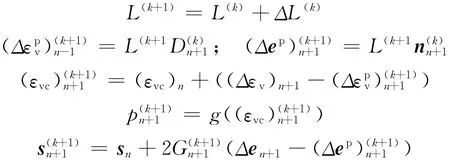
（5）檢查一致性條件殘余值：

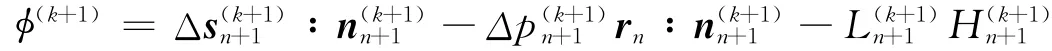
若｜φ（k＋1）｜＞tolerance，則未收斂，k＝k＋1，進(jìn)行步驟4；否則進(jìn)行第6步。

（6）更新應(yīng)力和內(nèi)變量：

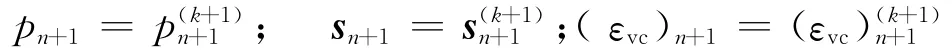
對于半顯式的Cutting Plane積分算法，其四階剛度張量如下：

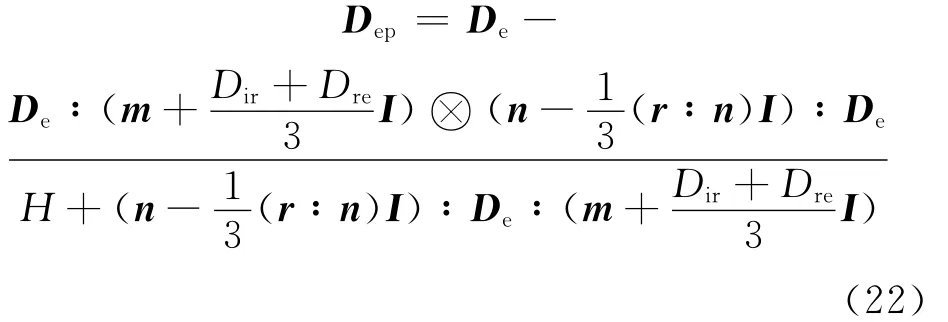
其中De為彈性剛度張量。

2．3 邊界面上應(yīng)力投影點(diǎn)求解算法

在應(yīng)力積分的第3和第4步中，需要求解應(yīng)力在邊界面上的投影，即求解式9中的β。為此采用Dowel和Jarratt［18］提出的Pegasus求根算法，該算法能夠保證快速無條件收斂，具體步驟如下：

（1）初始化試探值β0＝0和β1＝1。

（2）計(jì)算

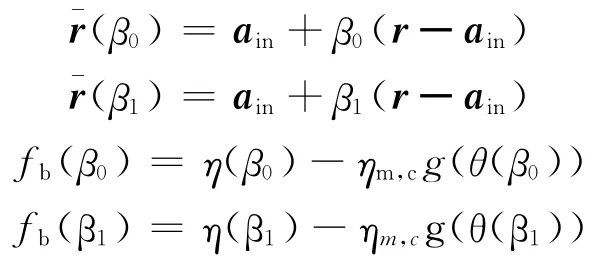
（4）計(jì)算

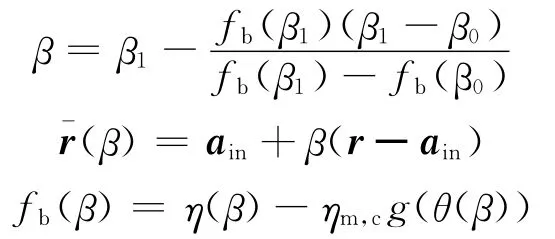
若｜fb（β）｜＜tolerance，計(jì)算收斂；否則進(jìn)行第5步。

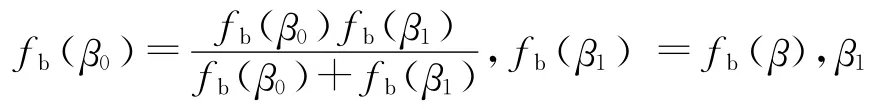
通過上述算法，目前已經(jīng)在 OpenSees 2．4．0版本中加入了三維化的模型。為了增加初始靜應(yīng)力場計(jì)算時(shí)模型的數(shù)值穩(wěn)定性，添加了彈性材料階段，具體使用方法可參見OpenSees網(wǎng)站中該模型說明文檔（http：／／opensees．berkeley．edu）。

3 三維化模型及算法的應(yīng)用

利用OpenSees中已有的用基于飽和土動力固結(jié)理論的完全耦合單元，使用本模型對飽和砂土不排水循環(huán)扭剪試驗(yàn)進(jìn)行模擬，并通過一個三維傾斜地基動力反應(yīng)分析驗(yàn)證模型及相應(yīng)數(shù)值算法對于計(jì)算液化后大變形和處理三維問題的有效性。

3．1 內(nèi)華達(dá)砂不排水循環(huán)扭剪試驗(yàn)?zāi)M

對Kutter等［19］用內(nèi)華達(dá)砂進(jìn)行的不排水空心圓柱扭剪試驗(yàn)進(jìn)行模擬。內(nèi)華達(dá)砂的基本物性指標(biāo)為：Gs＝2．67；d50＝0．18mm；emax＝0．887；emin＝0．551。試驗(yàn)中所用砂土相對密度71%，采用等剪應(yīng)力幅值為56kPa進(jìn)行循環(huán)加載，圍壓198kPa。由于該試驗(yàn)?zāi)康闹皇怯脕眚?yàn)證王志良等［3］的模型和其他邊界面模型的有效性，因此彈性和塑性模量以及破壞參數(shù)均可由Kutter等［19］的試驗(yàn)報(bào)告中直接獲得；剪脹相關(guān)參數(shù)則采用相應(yīng)的參數(shù)確定方法估計(jì)。具體參見表1。

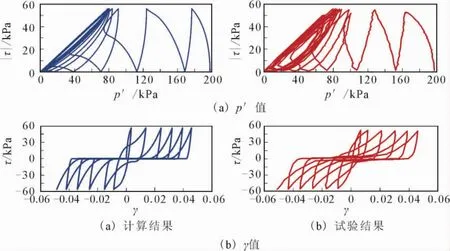
圖2 不同降雨量時(shí)水平位移等值線Fig．2 Horizontal displacement field at different rainfall level．

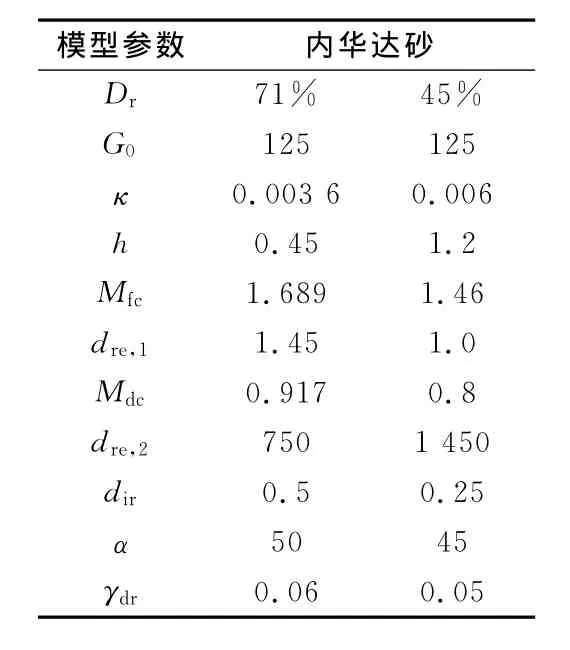
表1 模型參數(shù)取值Table 1 Parameter values in the model

圖2給出了對該試驗(yàn)的模擬結(jié)果，可以看到計(jì)算結(jié)果與試驗(yàn)結(jié)果的應(yīng)力路徑和應(yīng)力應(yīng)變關(guān)系吻合較好，尤其是對初始液化后應(yīng)力路徑和零有效應(yīng)力時(shí)產(chǎn)生的液化后大變形的模擬非常有效。

3．2 三維傾斜地基動力反應(yīng)分析

利用OpenSees中Brick UP［20］三維完全耦合單元，對一個10m傾斜地基進(jìn)行了三維動力反應(yīng)分析。如圖3所示，地基向y方向傾斜2°，地震動輸入沿x方向和z方向雙向輸入。模型網(wǎng)格由10個邊長1m的立方體單元組成，底面節(jié)點(diǎn)約束y向位移；為了模擬無限地基，將同層結(jié)點(diǎn)的三向自由度綁定；模型底面和側(cè)面為不排水面，地基表面排水，孔壓保持為零。土體采用VELACS離心模型試驗(yàn)［20］中使用的相對密度為45%的內(nèi)華達(dá)砂的參數(shù)。輸入地震波采用VELACS離心模型試驗(yàn)［21］模型1所使用的波形，豎向振幅設(shè)定為水平向的0．2倍。

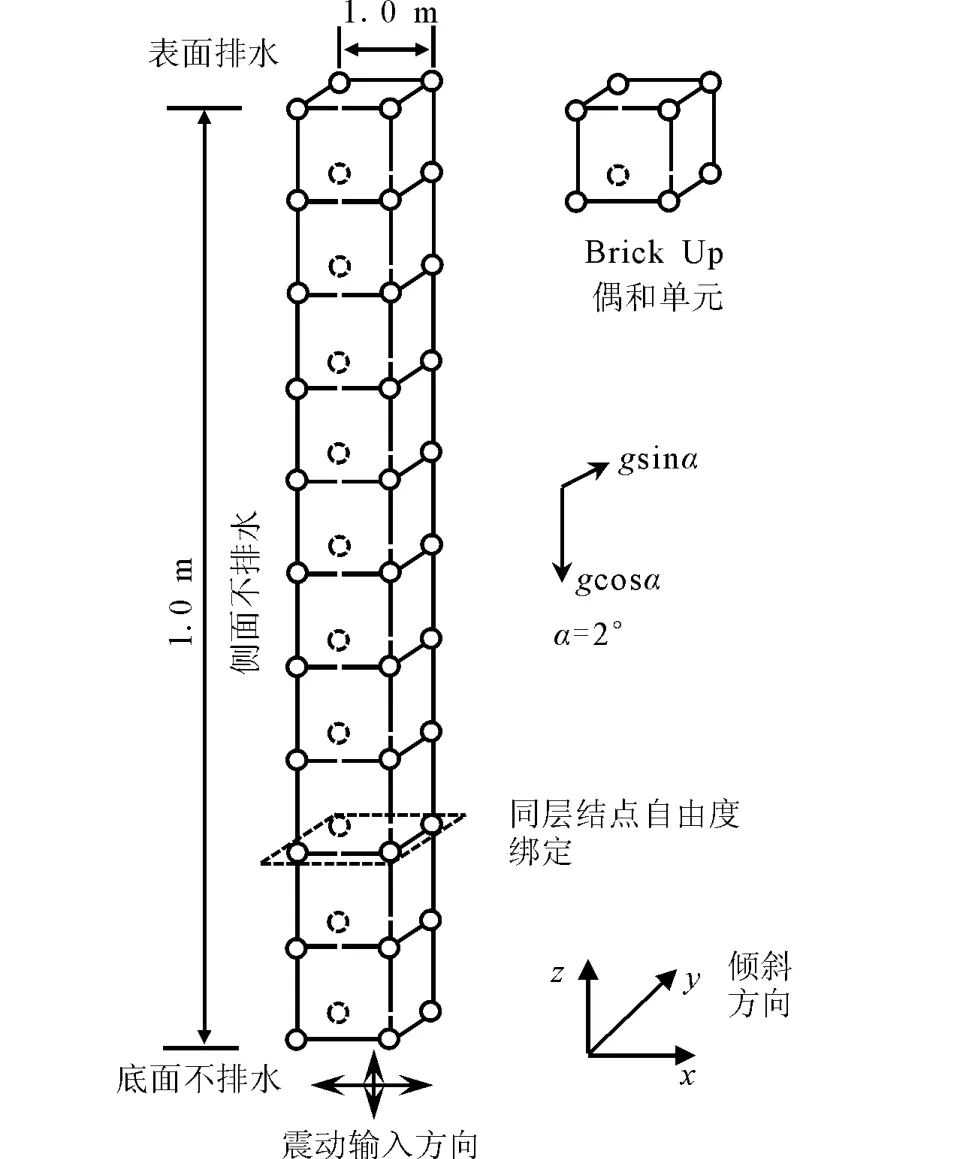
圖3 模型示意圖Fig．3 Schematic of model set up．

圖4給出了地震全過程不同時(shí)刻土體的變形和孔隙水壓力云圖。可以看出，在最初的2～3s內(nèi)土體尚未達(dá)到液化，地基變形較小。當(dāng)淺層土體孔壓累積至液化，地基開始向y方向變形，直至地震結(jié)束后在1m深處達(dá)到0．13m。圖5給出了1m深度處孔壓、x和y方向位移時(shí)程。超靜孔壓比在4s左右初次達(dá)到1，即初始液化。x方向位移隨著地震波而波動，但地震結(jié)束后殘余值幾乎為零；y方向位移則隨著超靜孔壓比接近1迅速累積。

對這一傾斜地基的三維動力反應(yīng)分析表明，本模型和相應(yīng)的數(shù)值算法能夠有效地計(jì)算三維條件下砂土的動力響應(yīng)和液化變形。

圖4 地震過程中土體變形（放大10倍）和孔壓云圖Fig．4 Soil deformation（amplified to 10times）and pore pressure contour during earthquake．

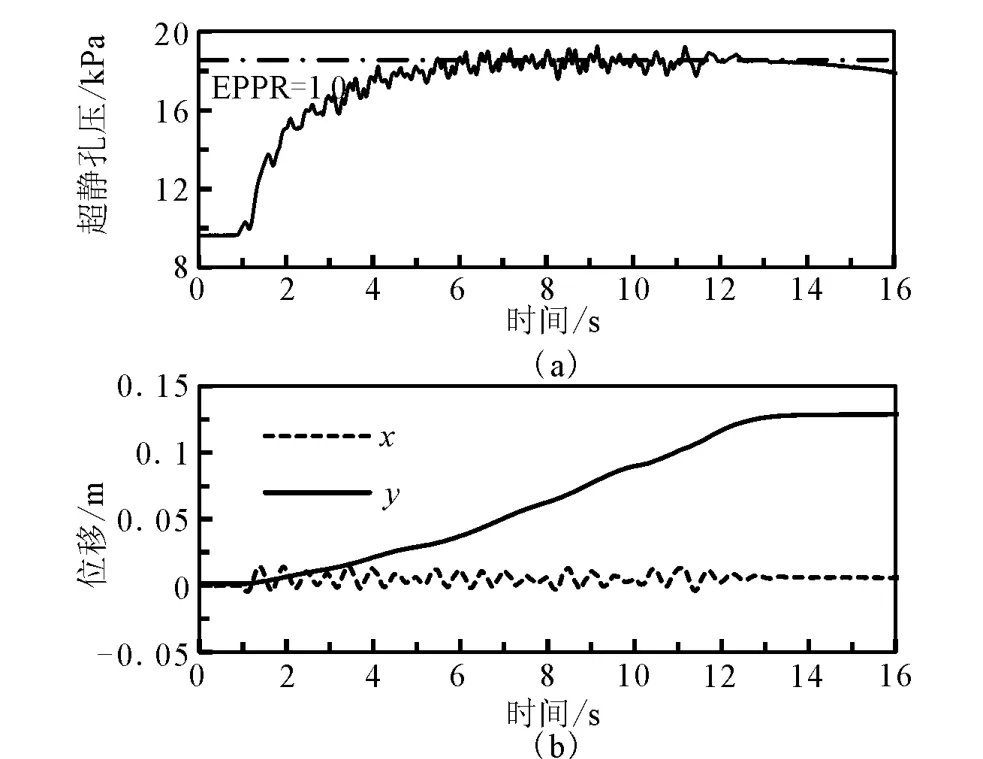
圖5 1m深度處孔壓及x和y方向位移時(shí)程Fig．5 Pore pressure and xand ydirection displacement history at 1mdepth．

4 結(jié)論

本文對基于符合砂土液化后大變形機(jī)理的彈塑性本構(gòu)框架，建立了三維應(yīng)力空間中砂土液化大變形本構(gòu)模型，實(shí)現(xiàn)了其數(shù)值化，并用于試驗(yàn)?zāi)M和三維動力反應(yīng)分析。

發(fā)展了在三維應(yīng)力空間中適合砂土液化后大變形本構(gòu)模型的邊界面和剪脹面上應(yīng)力映射規(guī)則，并相應(yīng)的定義了新的可逆性剪脹產(chǎn)生率。根據(jù)數(shù)值計(jì)算能力需求，調(diào)整了塑性流動方向和加載方向。實(shí)現(xiàn)了砂土液化后大變形本構(gòu)模型的三維化。

通過采用分子步的Cutting Plane數(shù)值積分算法實(shí)現(xiàn)模型應(yīng)力積分，并利用高效無條件收斂的Pegasus求根算法求解應(yīng)力投影，在OpenSees開源有限元平臺上實(shí)現(xiàn)了三維模型的數(shù)值化，對所有研究人員開放使用。

利用該模型，對內(nèi)華達(dá)砂不排水循環(huán)扭剪試驗(yàn)進(jìn)行模擬，驗(yàn)證了模型的模擬能力，尤其是在計(jì)算砂土液化后大變形方面的優(yōu)勢。通過對一個三維傾斜地基的動力反應(yīng)分析，顯示了模型及相應(yīng)數(shù)值算法在處理三維問題上的有效性。

［1］ Seed H B．Soil liquefaction and cyclic mobility evaluation for level ground during earthquakes［J］．Journal of the Geotechnical Engineering Division，1979：105（2）：201－255．

［2］ Hamada M．Large Ground Deformations and their Effects on Lifelines：1964Niigata Earthquake．Case Studies of Liquefaction and Lifelines Performance during Past Earthquake［R］．Buffalo：National Centre for Earthquake Engineering Research，1992：NCEER－92－0001．

［3］ Wang Z L，Dafalias Y F，Shen C K．Bounding surface hypoplasticity model for sand［J］．Journal of Engineering Mechanics，1990，116（5）：983－1001．

［4］ Papadimitriou A G，Bouckovalas G D，Dafalias Y F．Plasticity model for sand under small and large cyclic strains［J］．Journal of Geotechnical and Geoenvironmental Engineering，2001，127（11）：973－983．

［5］ Dafalias Y F，Manzari M T．Simple plasticity sand model accounting for fabric change effects［J］．Journal of Engineering Mechanics，2004，130（6）：622－634．

［6］ Mroz Z，Norris V A，ZienkiewtczОC．An anisotropic hardening model for soils and its application to cyclic loading［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1978，3（2）：203－221．

［7］ Yang Z，Elgamal A，Parra E．Computational model for cyclic mobility and associated shear deformation［J］．Journal of Geotechnical and Geoenvironmental Engineering，2003，129（12）：1119－1127．

［8］ Pastor M，Zienkiewicz O C，Chan A．Generalized plasticity and the modelling of soil behavior［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1990，14（3）：151－190．

［9］ Shamoto Y，Zhang J M．Mechanism of large post－liquefaction deformation in saturated sands［J］．Soils and Foundations，1997，2（37）：71－80．

［10］ 張建民，王剛．砂土液化后大變形的機(jī)理［J］．巖土工程學(xué)報(bào)，2006，28（7）：835－840．

Zhang J M，Wang G．Mechanism of large post－liquefaction deformation in saturated sand［J］．Chinese Journal of Geotechnical Engineering，2006，28（7）：835－840．

［11］ Zhang J M，Wang G．Large post－liquefaction deformation of sand，part I：physical mechanism，constitutive description and numerical algorithm［J］．Acta Geotechnica，2012，7（2）：69－113．

［12］ 王剛，張建民．砂土液化大變形的彈塑性循環(huán)本構(gòu)模型［J］．巖土工程學(xué)報(bào)，2007，29（1）：51－59．

Wang G，Zhang J M．A cyclic elasto－plastic constitutive model for evaluating large liquefaction－induced deformation of sand［J］．Chinese Journal of Geotechnical Engineering，2007，29（1）：51－59．

［13］ Dafalias Y F，Popov E P．A model of nonlinearly hardening materials for complex loading［J］．Acta Mechanica，1975，21（3）：173－192．

［14］ McKenna F，F(xiàn)enves G L．OpenSees Manual［EB／OL］．PEER Center，http：／／OpenSees．berkeley．edu．2001．

［15］ Richart F E，JR，HALL J R，Woods R D．Vibrations of soils and foundations［M］．Englewood Cliffs，N．J．：Prentice－Hall．Inc．，1970．

［16］ Zhang J M．Cyclic critical stress state theory of sand with its application to geotechnical problems［R］．Tokyo：Research Report of Tokyo Institute of Technology，1997：1－269．

［17］ Simo J C，Ortiz M．A unified approach to finite deformation elastoplastic analysis based on the use of hyperelastic constitutive equations［J］．Computer Methods in Applied Mechanics and Engineering，1985，49（2）：221－245．

［18］ Dowell M，Jarratt P．The"Pegasus"method for computing the root of an equation［J］．Bit Numerical Mathematics，1972，12（4）：503－508．

［19］ Kutter B L，Chen Y，Shen C K．Triaxial and torsional shear test results for sand［R］．CR 94．003－SHR，Port Hueneme，California：Naval Facilities Engineering Service Center，Contact Report，1994．

［20］ Yang Z，Lu J，Elgamal A．OpenSees soil models and solidfluid fully coupled elements user manual［M］．San Diego，California：University of California，2008．

［21］ Taboada V M，Dobry R．Experimental results of Model No．1at RPI［A］∥Proceedings of International Conference on Verification of Numerical Procedures for the Analysis of Soil Liquefaction Problems［C］．［S．l．］：［s．n．］，1993，3－17．