P－SV波斜入射時成層半空間自由場的時域算法①

趙 密，杜修力，劉晶波，韓 強

（1．北京工業大學城市與工程安全減災教育部重點實驗室，北京 100124；2．清華大學土木工程系，北京 100084）

0 引言

地震作用下土與結構動力相互作用分析中，首先需要計算地震自由波場作為波動輸入［1］。在自由場計算中，入射地震波可以簡化為豎直入射或者傾斜入射的平面體波，場地可以簡化為彈性均勻半空間或者彈性成層半空間。在一般工程結構的地震反應分析中，可以采用地震波豎直入射的均勻半空間或者成層半空間場地模型，該問題是空間一維的，能夠方便地在時域內求解。對于高壩、核電站、大型地下結構等重大工程結構，則需要考慮地震波傾斜入射引起的場地運動非一致變化對結構地震反應的影響。地震波斜入射時，均勻半空間自由場可以根據波動傳播規律在時域內計算［2－4］；而成層半空間自由場只能采用解析方法在頻域內求解［5］，為了獲得時域反應需要多次執行快速傅里葉變換，因而需要大量的計算時間和存儲空間。

為了在時域內計算地震波斜入射時成層半空間自由波場，劉晶波和王艷［7－9］提出了一種簡便易行的空間一維化計算方法。該方法采用矩形有限單元進行網格虛擬劃分，豎直方向采用滿足波動精度要求的網格尺寸；水平方向的網格尺寸等于時間步長與水平視波速的乘積。基底設置黏性人工邊界條件［10］模擬基巖半空間的輻射阻尼，并將波動輸入轉化為等效荷載施加在人工邊界結點上。將集中質量有限元法和時間中心差分相結合建立結點運動方程組。然后根據斯奈爾定律，將水平方向相鄰結點的運動用該結點相鄰時刻的運動表示，從而將求解結點運動的空間二維方程組化為空間一維方程組。求解此方程組，即得到自由波場中豎向一列結點的運動。最后根據行波傳播的特點，可方便地確定整個空間的自由波場。這樣，計算地震波斜入射時水平成層半空間自由場的空間二維問題轉化為簡單的空間一維問題。

對于出平面SH波問題［6］，修正的黏性邊界能夠完全吸收外行波，精確模擬基巖半空間的輻射阻尼；然而對于平面內P－SV波問題［7－8］，黏性邊界及其修正形式均不能完全吸收外行波，形成的虛假反射波將污染自由場反應。地震波傾斜入射角越大，計算結果與真實波場之間的誤差越大。實際上，黏性邊界［10］、黏彈性邊界［11－12］、多次透射公 式［13］、高精度人工邊界條件［14－15］均不能精確和高效地模擬該問題中基巖半空間的輻射阻尼。本文利用平面內波動問題中外行波是傳播方向已知的平面P波和SV波這一波動特性，提出一種適用于該問題的精確人工邊界條件，應用該條件替代黏性邊界，建立PSV波斜入射時成層半空間自由場的一維化時域算法。

1 人工邊界和地震荷載

地震波（平面P－SV波）斜入射時成層半空間波動問題如圖1所示。水平成層介質位于半空間上，成層介質表面滿足應力為零的自由邊界條件，各層介質交界面處滿足位移和應力連續條件。第j（1…N）層彈性均勻介質的厚度為hj，密度為ρi，λi拉梅常數為 和Gj。下部彈性均勻半空間的密度為ρ，拉梅常數為λ和G。平面P波或者SV波從半空間無限遠處向右上方傾斜入射，入射角為θ。在計算中，將下部半空間截去，此時第N層介質與半空間的交界面為人工邊界，本節建立能夠精確模擬下部半空間輻射阻尼的人工邊界條件，給出人工邊界處入射波的等效荷載。

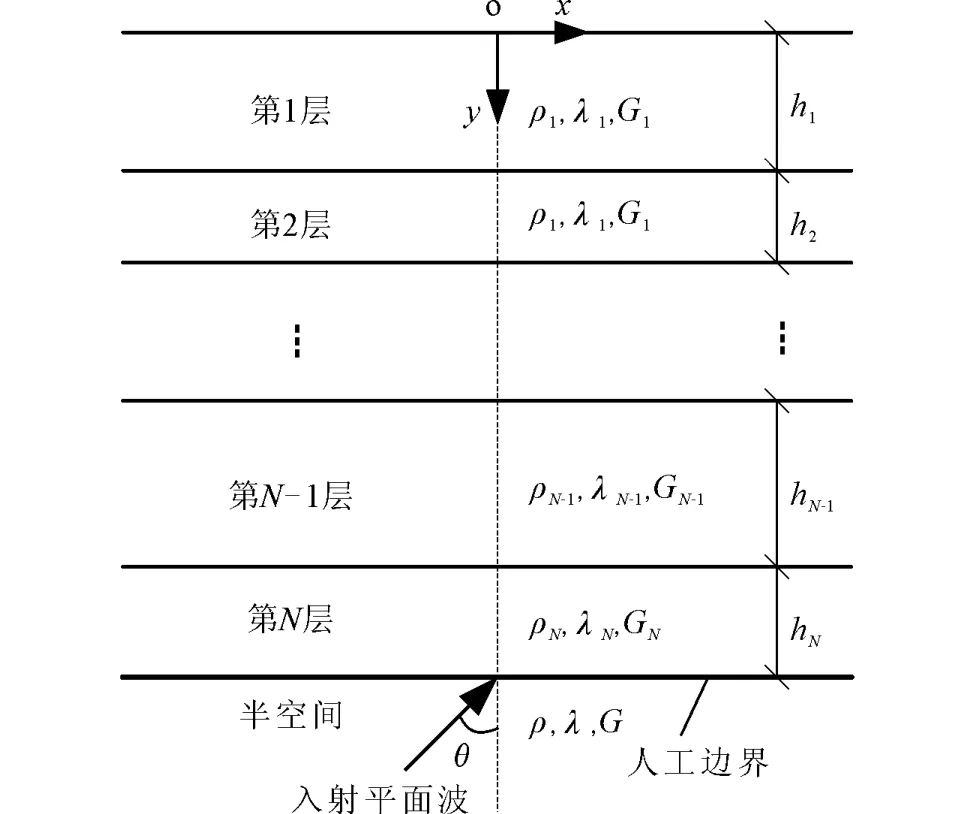
圖1 地震波斜入射時成層半空間波動問題Fig．1 Wave propagation problem in layered half space under seismic wave of oblique incidence．

1．1 精確的人工邊界條件

半空間內向無窮遠處傳播的外行波由平面P波和平面SV波構成，兩者的勢函數可以分別表示為

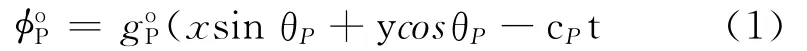
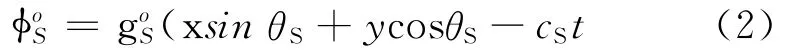
當P波入射時，θP＝θ，可由式（3）確定θS；當SV 波入射時，θS＝θ，可由式（3）確定θP。位移的勢函數表達式為

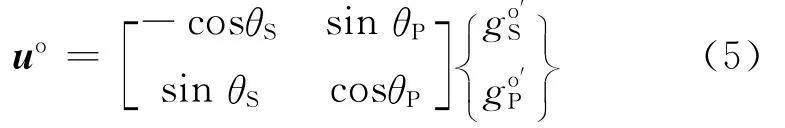
其中，上標撇號表示波形函數的導數。

對式（5）求時間偏導數，得到速度向量為

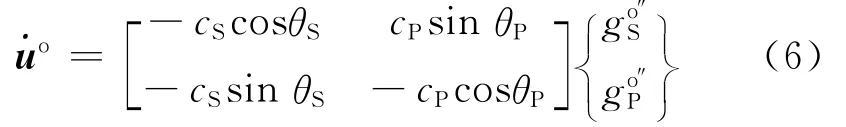
其中，變量上方的點號表示時間導數。彈性均勻介質的應力－位移本構關系為

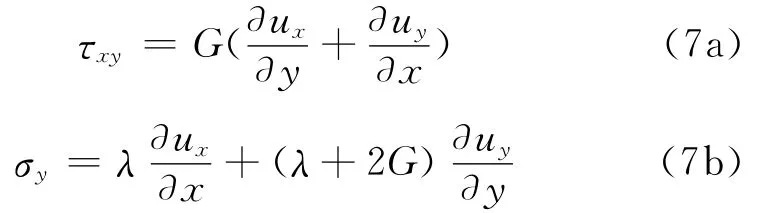
對于外行波，將位移式（5）代入式（7）得到應力向量為

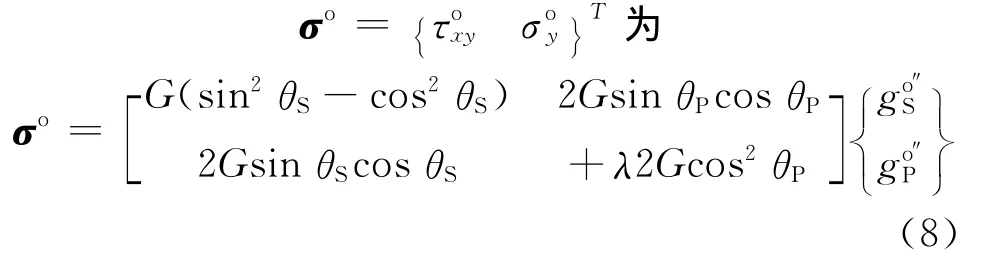
聯立式（6）和（8），消去波形函數得

其中，阻抗矩陣為

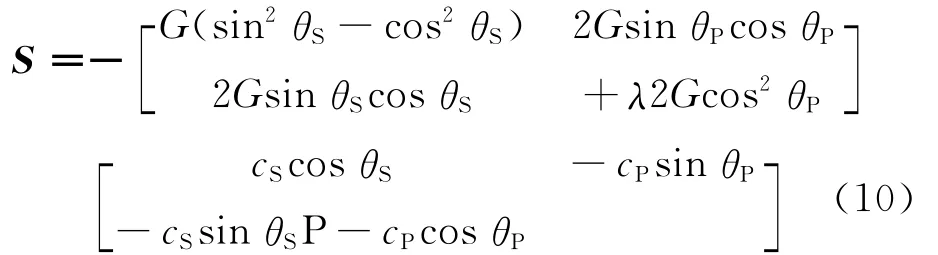
在人工邊界處，式（9）是精確的人工邊界條件，它由邊界速度計算半空間作用于成層介質的應力。有限元計算中，該邊界條件可以采用集中離散方式實現。可以看到，對于不同的人工邊界結點，本文邊界條件是空間解耦的；但對于每個結點的兩個自由度，本文邊界條件是耦聯的，這一點與黏性邊界不同，正是耦聯特性保證本文邊界條件能夠精確地同時吸收外行P波和SV波。

1．2 人工邊界上的地震荷載

本節給出尚未施加人工邊界條件時，入射波在人工邊界處的等效荷載。

1．2．1 平面P波入射情況入射平面P波的勢函數為

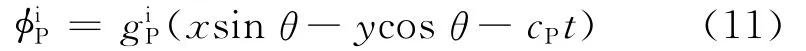
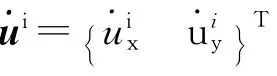
如果規定入射波合速度的正方向與入射波傳播方向一致，則在人工邊界和y軸交點處已知的入射P波合速度時程可以表示為

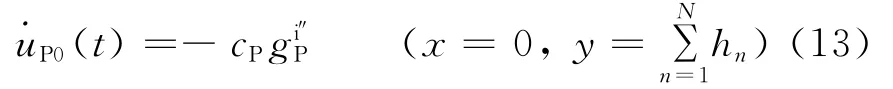
聯立式（12）和（13），消去波形函數得

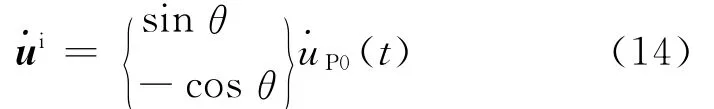
對于入射波，將式（11）代入式（4），然后代入式（7），得入射波作用下半空間作用于成層介質的應力向量

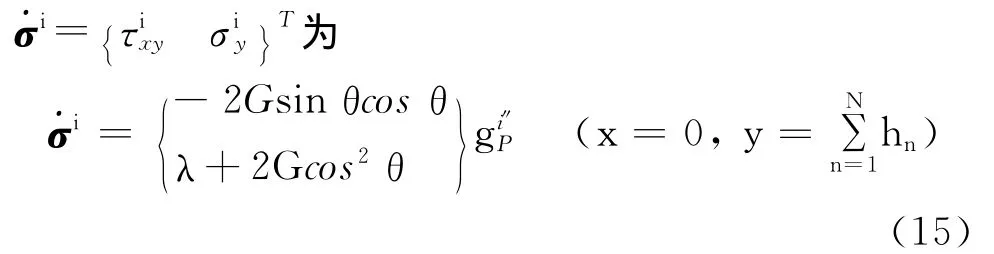
聯立式（13）和（15），消去波形函數得

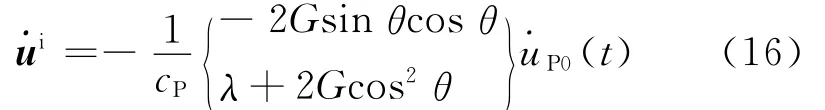
1．2．2 平面SV波入射情況

入射平面SV波的勢函數為

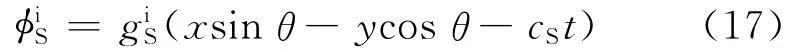
其中，上標i表示入射波；是任意波形函數。

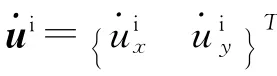
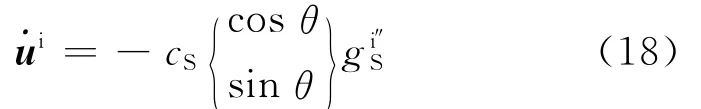
如果規定入射波合速度的正方向為入射波傳播方向順時針旋轉90°角的方向，則在人工邊界和y軸交點處已知的入射SV波合速度時程可以表示為

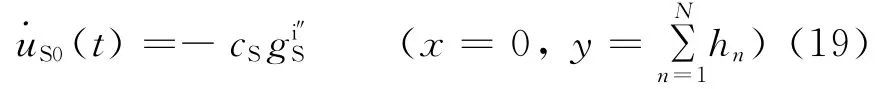
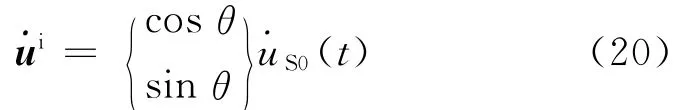
對于入射波，將式（17）代入式（4），然后代入式（7），得入射波作用下半空間作用于成層介質的應力向量為

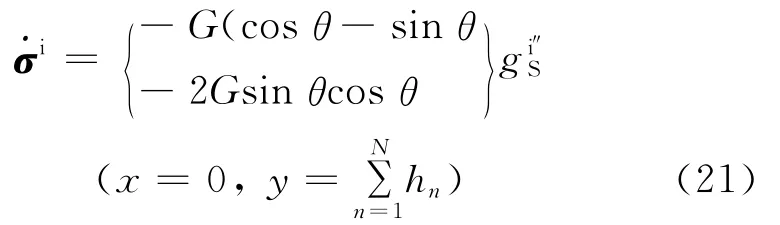
聯立式（19）和（21），消去波形函數得

2 有限元結合中心差分的一維化算法

對于半空間上部的N層介質，采用矩形四結點雙線性平面應變有限單元進行虛擬網格劃分，沿y軸方向的單元尺寸Δy為，沿x軸方向的單元尺寸為Δx，時間步長為 。x＝0列結點p時刻的集中質量有限元方程為

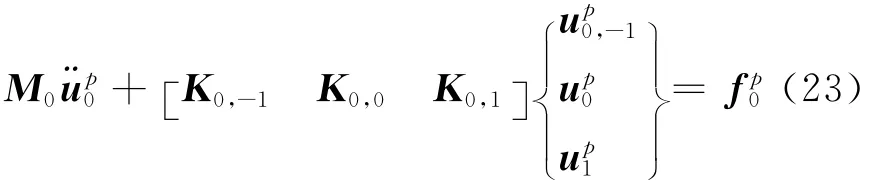
人工邊界處波場滿足疊加原理，可以分解為外行波場和入射波場，x＝0處人工邊界結點的荷載和速度可以分別寫為

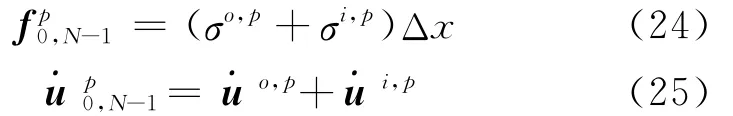
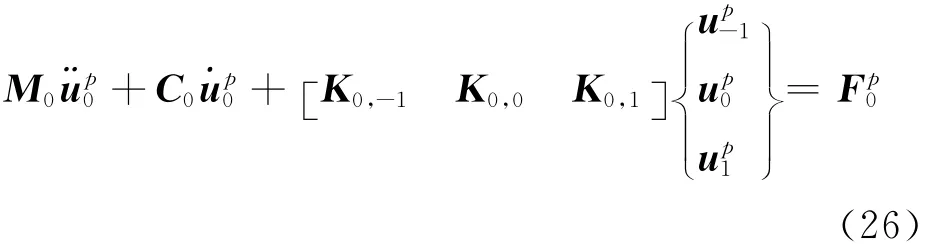
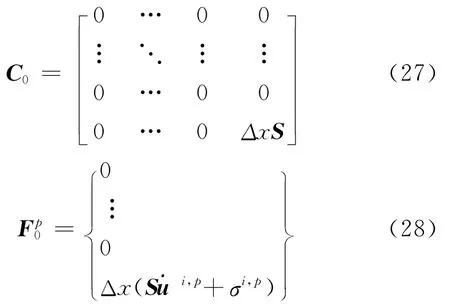
時間導數的中心差分公式為

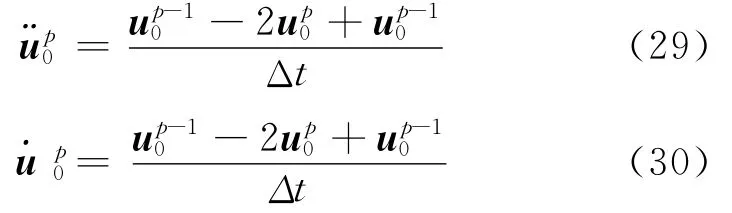
成層半空間中的平面波服從斯奈爾定律，即全部平面波的水平方向視波速相等。如果取水平方向的有限元尺寸Δx等于時間步長Δt與水平視波速cx的乘積，即Δx＝cxΔt。則根據斯奈爾定律，x＝0列結點p＋1時刻的位移可以用x＝－Δx列結點p時刻的位移表示，x＝0列結點p－1時刻的位移可以用x＝Δx列結點p時刻的位移表示，即

這樣，空間二維問題能夠被轉化為簡單的空間一維問題。將式（29）～（32）代入式（26），整理得到x＝0列結點從前兩時刻位移遞推當前時刻位移的線性代數方程組

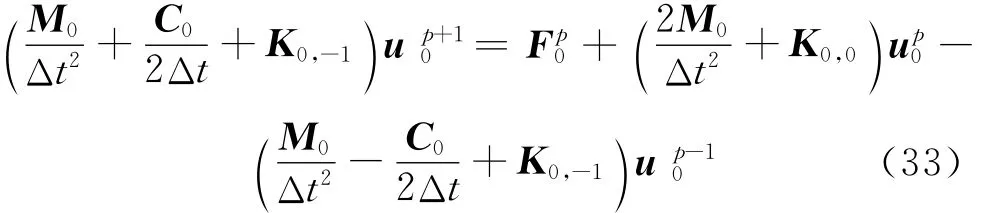
式（33）的初始值為

逐個時刻的求解式（33），可以得到自由波場中豎向一列結點的運動。根據波動水平方向視速度相等的特點，可以方便地確定整個空間的自由波場。

豎直方向有限元尺寸Δy應滿足波動精度要求。確定時間步長Δt的數值穩定性條件，以及方法的精度分析見文獻［7－9］。

3 數值算例

為了驗證本文改進方法的精度和有效性，分析半空間基巖表面覆蓋單層土問題，該算例也見文獻［9］的3．8節。土層厚度為50m，質量密度為1 000 kg／m3，P 波 波 速 為 346m／s，SV 波 波 速 為 200 m／s。基巖的質量密度為1 500kg／m3，P波波速為866m／s，SV波波速為500m／s，人工邊界截去地表深度100m以下的基巖，即保留厚度50m的基巖作為有限元區域。在人工邊界和y軸交點處入射波位移時程如圖2所示。深度方向的空間步距為5 m，滿足數值穩定性條件的時間步長為0．005s。

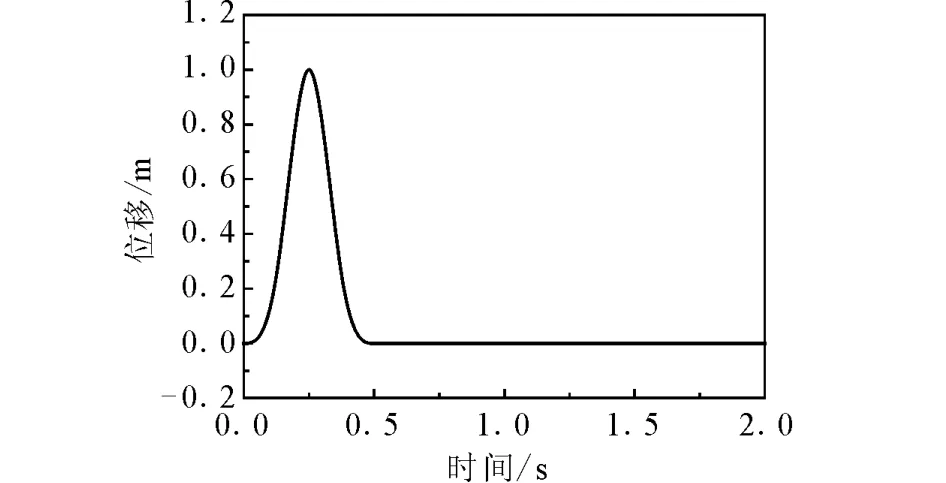
圖2 入射波位移時程Fig．2 Time history of displacement of incident wave．

首先研究平面P波斜入射情況。文獻［7，9］的研究表明，入射角越大，應用黏性邊界的自由場算法的精度越低，限于篇幅，本文僅研究60°角大角度入射的情況。圖3給出P波60°角入射時地表（坐標原點）的位移時程結果，其中理論解是采用頻域傳遞矩陣法［5］結合快速傅里葉變換得到的。為了更清楚地觀察本文方法相對于劉晶波－王艷（Liu－Wang）方法［7－9］的改進效果，圖3也給出了兩種方法計算結果相對于理論解的誤差，即每種方法結果與理論解的差的絕對值。可以看到，新方法的計算結果與理論解吻合良好，而Liu－Wang方法的計算誤差相對較大，說明本文人工邊界條件能夠進一步提高P波大角度入射時平面內自由場一維化時域算法的精度。

當平面SV波斜入射時，本文僅考慮入射角小于臨界角的情況，即自由波場中僅含有均勻平面波的情況。與P波入射類似，本文研究SV波30°角入射的情況。圖4給SV波30°角入射時地表（坐標原點）的位移時程結果，其中理論解同樣是采用頻域傳遞矩陣法［5］結合快速傅里葉變換得到。圖4也給出了本文新方法計算結果和Liu－Wang方法［8－9］計算結果相對于理論解的誤差。可以看到，新方法的計算結果與理論解吻合良好，而Liu－Wang方法的計算誤差相對較大，說明本文人工邊界條件能夠進一步提高SV波大角度入射時平面內自由場一維化時域算法的精度。

圖3 P波60°角入射時地表位移時程Fig．3 Time history of displacement on ground surface under P wave of 60°angle incidence．

4 結語

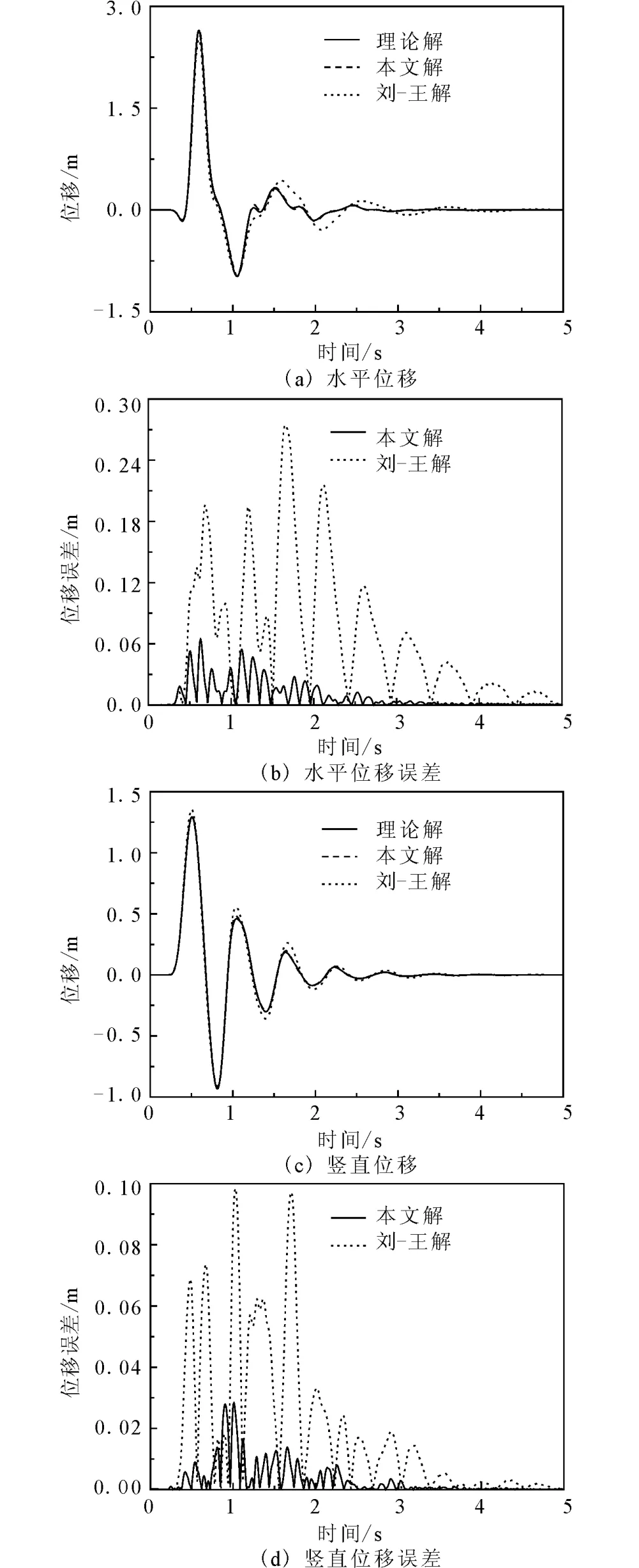
圖4 SV波30°角入射時地表位移時程Fig．4 Time history of displacement on ground surface under SV wave of 30°angle incidence．

劉晶波和王艷［6－9］建立了一種在時域內計算地震波斜入射時成層半空間瞬態自由場的數值方法。本文對該方法進行了改進，提出一種新的精確人工邊界條件替代黏性邊界，解決了平面P－SV波大角度入射時由于底部吸收邊界條件精度低而導致整套自由場時域算法精度降低的問題。本文考慮自由波場中僅含有均勻平面波的情況，自由波場中含有非均勻平面波和面波的波動問題有待深入研究。

［1］ Wolf J P．Dynamic Soil－Structure Interaction［M］．Englewood Cliffs：Prentice－Hall，1985．

［2］ 徐海濱，杜修力，趙密，等．地震波斜入射對高拱壩地震反應的影響［J］．水力發電學報，2011，30（6）：159－165．

XU Hai－bin，DU Xiu－li，ZHAO Mi，et al．Effect of Oblique Incidence of Seismic Waves on Seismic Responses of High Arch Dam［J］．Journal of Hydroelectric Engineering，2011，30（6）：159－165．

［3］ 苑舉衛，杜成斌，劉志明．地震波斜入射條件下重力壩動力響應分析［J］．振動與沖擊，2011，30（7）：120－126．

YUAN Wei－ju，DU Chen－bin，LIU Zhi－ming．Time－domain Seismic Response for Gravity Dam to Obliquely Incident and Seismic Waves［J］．Journal of Vibration and Shock，2011，30（7）：120－126．

［4］ 郜新軍，趙成剛，劉秦．地震波斜入射下考慮局部地形影響和土結動力相互作用的多跨橋動力響應分析［J］．工程力學，2011，28（11）：237－243．

GAO Xin－jun，ZHAO Cheng－gang，LIU Qin．Seismic Response Analysis of Multi－span Viaduct Considering Topographic Effect and Soil－structure Dynamic Interaction Based on Inclined Wave［J］．Engineering Mechanics，2011，28（11）：237－243．

［5］ 傅淑芳，劉寶誠．地震學教程［M］．北京：地震出版社，1991．

FU Shu－fang，LIU Bao－cheng．Seismology Tutoria［M］l．Beijing：Seismic Press，1991．

［6］ 劉晶波，王艷．成層半空間出平面自由波場的一維化時域算法［J］．力學學報，2006，38（2）：219－225．

LIU Jing－bo，WANG Yan．A 1－D Time－domain Method for 2－D Wave Motion in Elastic Layered Half－space by Antiplane Wave Oblique Incidence［J］．Chinese Journal of Theoretical and Applied Mechanics，2006，38（2）：219－225．

［7］ 劉晶波，王艷．成層介質中平面內自由波場的一維化時域算法［J］．工程力學，2007，24（7）：16－22．

LIU Jing－bo，WANG Yan．A 1DTime－domain Method for Inplane Wave Motion of Free Field in Layered Media［J］．Engineering Mechanics，2007，24（7）：16－22．

［8］ LIU Jing－bo，WANG Yan．A 1DTime－domain Method for inplane Wave Motions in A Layered Half－space［J］．Acta Mechanica Sinica，2007，23：673－680．

［9］ 王艷．非一致地震動場數值方法研究及在結構動力分析中的應用［D］．北京：清華大學，2007．

WANG Yan．Research on the Numerical Method for Asynchronous Seismic Wave Motions and Its Application in Dynamic Analysis of Structures［D］．Beijing：Tsinghua University，2007．

［10］ Lysmer J，Kulemeyer R ．Finite Dynamic Model for Infinite Media［J］．Journal of Engineering Mechanics，ASCE，1969，95：759－877．

［11］ LIU Jing－bo，LüYan－dong．A Direct Method for Analysis of Dynamic Soil－structure Interaction Based on Interface Idea［A］／／Proceedings of the Chinese－Swiss Workshop on Dynamic Soil－Structure Interaction［C］．Beijing：International Academic Publishers，1997．

［12］ 杜修力，趙密，王進廷．近場波動模擬的人工應力邊界條件［J］．力學學報，2006，38（1）：49－56．

DU Xiu－li，ZHAO Mi，WANG Jin－ting．A Stress Artificial Boundary in FEA for Near－field Wave Problem［J］．Chinese Journal of Theoretical and Applied Mechanics，2006，38（1）：49－56．

［13］ 廖振鵬．工程波動理論導論（第二版）［M］．北京：科學出版社，2002．

LIAO Zhen－peng．Introduction to Wave Motion Theories for Engineering（Second Edition）［M］．Beijing：Science Press，2002．

［14］ DU Xiu－li，ZHAO Mi．A local Time－domain Transmitting Boundary for Simulating Cylindrical Elastic Wave Propagation in Infinite Media［J］．Soil Dynamics and Earthquake Engineering，2010，30（10）：937－946．

［15］ ZHAO Mi，DU Xiu－li，LIU Jing－bo，et al．Explicit Finite Element Artificial Boundary Scheme for Transient Scalar Waves in Two－dimensional Unbounded Waveguide［J］．International Journal for Numerical Methods in Engineering，2011，87（11）：1074－1104．