罕遇地震下空心薄壁高墩大跨T形剛構橋彈塑性地震反應分析①

李 林

（蘭州鐵道設計院有限公司，甘肅 蘭州 730000）

0 引言

受地形條件控制，鐵路橋梁在跨越高山峽谷時往往需要采用高墩大跨結構。由于T形剛構橋具有跨越能力大、結構受力合理、墩梁固結無需巨型支座、整體剛度大且施工方便等特點，近年來在我國西北黃土高原地區得到廣泛應用。為滿足鐵路橋梁的剛度要求和經濟性要求，高于30m的橋墩一般均采用薄壁空心截面形式的鋼筋混凝土橋墩。5·12汶川大地震后，高烈度地震區大跨度橋梁的抗震設計得到充分重視。我國最新修訂版的《鐵路工程抗震設計規范》（GB50111－2006）［1］在設防理念上采用了分級設防的思想，即根據地震動概率水準的不同制定不同的設防目標，具體而言就是“小震不壞、中震可修、大震不倒”的三水準抗震設計要求。規范中明確規定：對于重要橋梁，在罕遇地震作用下應按非線性時程反應分析法［2］對鋼筋混凝土橋墩進行延性驗算或最大位移分析。但鐵路規范中對于彈塑性分析方法中的計算模型及相關參數選取則沒有具體的規定及缺乏指導。在罕遇地震下薄壁空心高墩大跨T構鐵路橋的抗震性能是否滿足“大震不倒”的要求需要得到確認，因此深入研究此類橋梁在罕遇地震下的抗震性能十分必要。

目前國內對于采用薄壁空心高墩大跨T構鐵路橋關于延性抗震方面的研究文獻較少。對于同類橋梁，《歐洲橋梁抗震設計規范》建議設計成有限延性或基本彈性；文獻［3］對國內外橋梁延性抗震構造設計方面作了比較；文獻［4］采用Pushover分析方法計算結構位移延性能力；文獻［5］用設置多個塑性鉸的分析模型研究連續剛構橋的彈塑性地震反應。

T形剛構橋由于在墩頂與梁底處采用固結，在罕遇地震作用下可能在墩頂與墩底均形成塑性鉸，進入彈塑性受力狀態，因此需要計入非線性塑性變形的耗能影響對結構進行抗震分析并做延性設計，以達到抗震性能要求Ⅲ的設防目標。鑒于彈塑性地震響應分析的復雜性，本文以一座（96＋96）m空心薄壁高墩大跨T形剛構鐵路橋為工程背景實例，在前人研究成果的基礎上，使用有限元軟件，利用PM集中塑性鉸單元及Takeda武田三線型滯回模型進行罕遇地震作用下非線性動態時程彈塑性地震反應分析，并進行相應的抗震性能評價，旨在對同類鐵路橋梁結構的延性抗震具體計算分析方法提供參考和借鑒作用。

1 工程背景

某一在建特大橋工程位于寧夏固原市原州區東北部一條單線地方鐵路上，橫跨一深切沖溝，溝槽深約76m。主橋采用96＋96m預應力混凝土T形剛構橋。橋址位于Ⅷ度地震區，動峰值加速度Ag＝0．30g，場地土特征周期Tg＝0．4s，屬于II類場地。主橋立面圖見圖1。

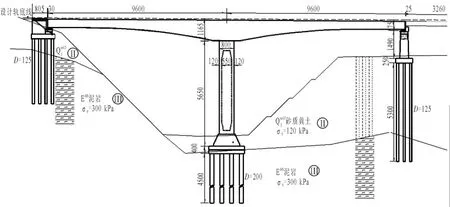
圖1 主橋立面布置圖（單位：cm）Fig．1 The elevation layout of main bridge（unit：cm ）．

上部結構主梁為變截面預應力混凝土箱梁，單箱單室結構。頂板寬7．5m，底寬5．0m，主墩支點截面處梁高11．0m，跨中截面梁高4．5m，頂板厚0．46m，主墩支點截面處底板厚1．3m，跨中截面底板厚0．5m，梁高和底板厚度自根部至兩端均呈1．8次拋物線變化，墩頂箱梁設置2．0m橫隔板2道，梁端設置2．5m厚的橫隔板1道。采用縱、橫、豎三向預應力體系。主橋橋墩采用變截面矩形薄壁墩，4×6根Φ2m的鉆孔灌注樁基礎。墩高50m，墩身順橋向厚度8．0m，壁厚1．2m，內外壁為直坡變化；墩頂橫橋向寬度7．5m，壁厚為1．2m，墩身橫橋外側按40：1、內側按60：1的坡度變化，墩底橫橋向寬度10．0m。主墩結構如圖2所示。

2 計算方法及地震波的選取

2．1 計算方法

時程分析法［2］計算結構在每個時刻的地震反應（內力和變形）。用此法進行計算時，當輸入地震波的作用較為強烈以至結構某些部位強度達到屈服進入塑性時，通過構件剛度的變化可求出彈塑性階段的結構內力與變形。這時結構薄弱層間位移可能達到最大值，從而造成結構的破壞直至倒塌。由于非線性分析的復雜性，計算分析時按如下假定：（1）上部結構為彈性，非線性行為只發生在下部橋墩中；（2）考慮“樁－土”作用，將地基土對結構的約束用彈簧來模擬，其剛度按m法計算；（3）橋墩進入非線性工作狀態的部位按照彈性狀態下初步計算的內力值分析確定。

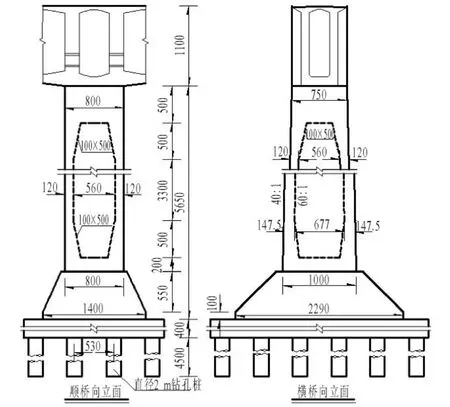
圖2 橋墩結構立面圖（單位：cm）Fig．2 The elevation layout of pier structure（unit：cm ）．

為真實的模擬橋梁結構的力學特性，利用大型結構分析軟件Midas／Civil建立空間梁單元計算模型，采用分段線性逐步積分法對該橋進行彈塑性地震反應分析。恢復力滯回模型采用常用的Takeda武田三線型模型。由于橋墩空心部分更容易進入塑性狀態，因此在T構墩頂部和底部空心部分均設置塑性鉸［5］。塑性鉸的長度取截面計算方向的尺寸，塑性鉸區單元用彈塑性梁單元來模擬，鉸類型采用能夠考慮軸力對鉸的彎曲屈服強度影響的P－M集中鉸。按照鐵路震規要求，在全橋罕遇地震分析過程中，在順橋向和橫橋向分別輸入地震波，不考慮豎向地震作用，同時不考慮活載組合，僅考慮恒載效應。結構離散計算模型見圖3。

2．2 地震波的選取

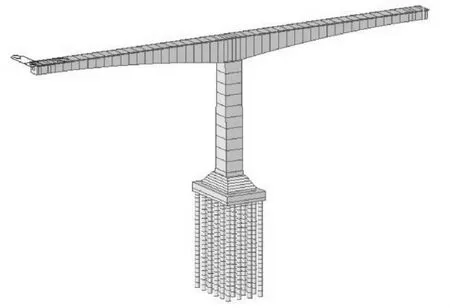
圖3 計算模型Fig．3 Analysis model．

輸入地震波的特性對時程分析結果有很大的影響，選擇的原則是使輸入地震波的特性和建筑場地的條件相符合［6］。地震波的峰值應反映橋址所在地區的烈度，而其頻譜組成應反映場地的卓越周期和動力特性。震規要求在對特殊結構進行時程分析時應選擇多條地震波進行分析比較。由于該橋沒有提供安評地震波，本文選擇了兩條國內外常用的強震記錄：El－centro波和Taft波。在輸入地震波加速度時，將各記錄的峰值進行了調整，使輸入的水平加速度峰值達到罕遇地震作用下對應Ⅷ度區的0．57 g，如圖4所示。

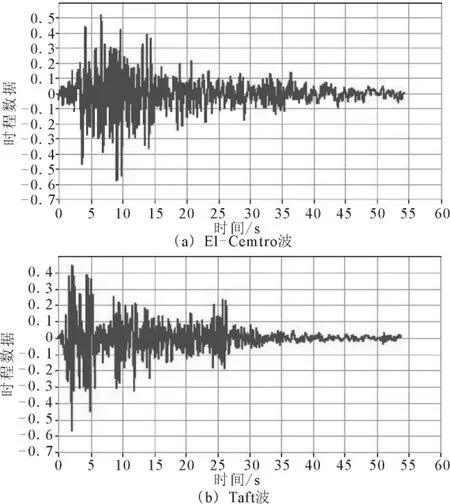
圖4 輸入的罕遇地震波Fig．4 The input waves of high－level earthquake．

3 彈塑性時程反應計算及結果分析

3．1 橋墩截面彎矩－曲率分析

在結構的彈塑性分析中，墩柱截面的非線性特性使用截面的彎矩－曲率關系曲線（Moment Curvature Curve）來描述。利用截面尺寸和實配鋼筋獲得截面的M－Φ曲線，同時使用該曲線可評價鋼筋混凝土截面的抗震性能。通過定義截面尺寸，選擇相應的材料本構模型，并輸入混凝土和鋼筋的性質及截面的軸向力，程序計算出截面的一些關鍵特性，例如屈服特性值、極限特性值等。對薄壁空心橋墩墩頂及墩底塑性鉸截面進行截面順橋向彎矩－曲率分析計算的結果見表1。

表1 截面彎矩－曲率關系

3．2 計算結果及分析

限于篇幅，文中只對加速度峰值為0．57g的兩條罕遇地震波在順橋向的地震反應進行彈塑性非線性時程分析，分別計算出兩條波作用下的墩頂位移、墩頂截面及墩底截面的內力及塑性鉸區域彎矩－曲率滯回曲線。為便于對比，同時又分別按照反應譜法［2］和線性動態時程法對結構進行了計算，計算結果見圖5～圖7及表2所示。

表2 罕遇地震下順橋向地震反應（α＝0．57g）

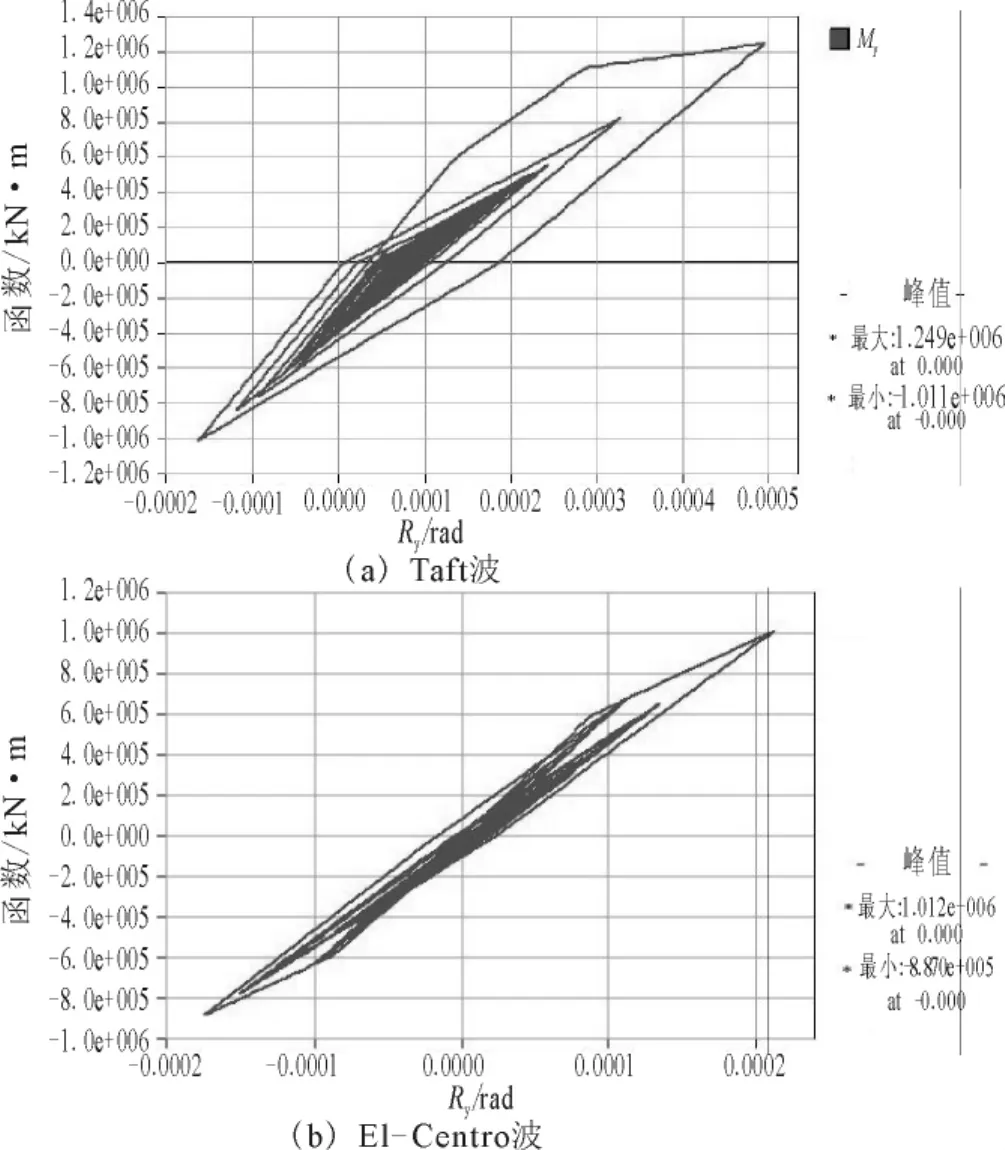
圖5 順橋向墩底彎矩－曲率滯回曲線Fig．5 Moment－curvature hysteretic curves at pier base along the bridge direction．

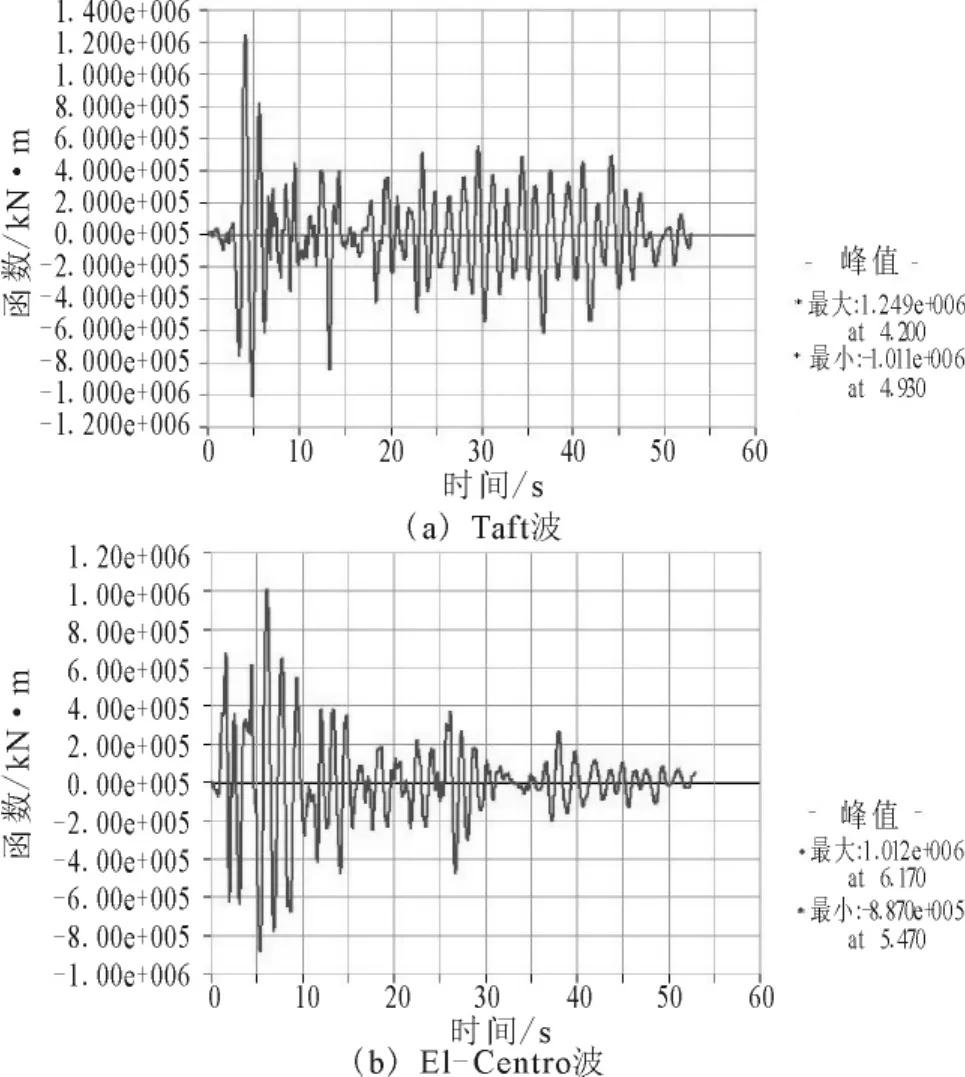
圖6 順橋向墩底彎矩反應時程Fig．6 The time history of moments at pier base along the bridge direction．

從表2的計算結果對比可看出，與線性時程分析和反應譜分析的計算結果相比，考慮彈塑性的非線性時程地震反應內力明顯減小，尤其是墩頂截面彎矩減小幅度最大，非線性時程計算的墩頂截面彎矩只有線性時程計算的1／3～1／2。

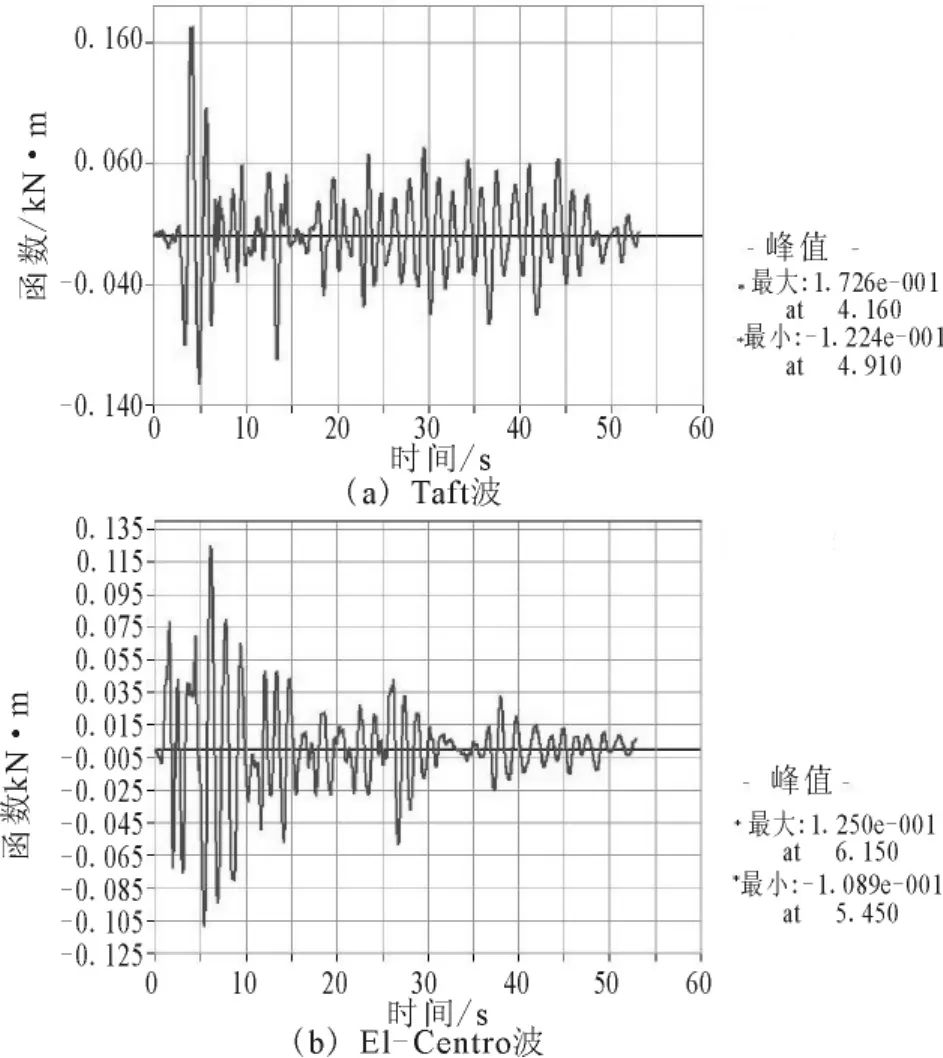
圖7 順橋向墩頂位移反應時程Fig．7 The time history of displacements at pier top along the bridge direction．

墩頂截面在El－Centro波和Taft波作用下，塑性鉸區均處于線彈性工作狀態，截面尚未進入開裂階段，離到達屈服階段尚遠，結構不會有損傷。

從墩底截面塑性鉸彎矩－曲率滯回曲線可以明顯看出，在El－Centro波作用下墩底截面已經進入開裂階段末段，但尚未進入屈服階段；在Taft波作用下墩底截面塑性鉸則已經進入塑性工作狀態，截面進入屈服階段但塑性反應幅度不大，結構損傷較小，遠未達到極限破壞狀態。Taft波引起的地震反應比El－Centro波相對要大。

3．3 位移反應驗算

根據截面彎矩－曲率關系表中墩底屈服彎矩為1．091E＋06kN·m，反算出對應墩頂順橋向的屈服位移為0．127m。El－Centro波作用下的非線性位移延性比μu＝0．125／0．127＝0．984；Taft波作用下的非線性位移延性比μu＝0．173／0．127＝1．362，均滿足規范“非線性位移延性比μu＜4．8”的要求。

由于文獻［1］附錄F．0．1－1提供了根據線性彎矩比來計算非線性位移延性比的簡化方法，這里也按照簡化方法作一驗證：

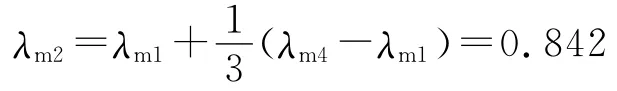
由此可以計算得到表3中橋墩非線性位移延性系數。

表3 非線性位移延性比

由上表可以看出文獻［1］提供的根據線性彎矩比來計算非線性位移延性比的簡化方法得出的結果與采用非線性時程計算的結果比較接近，說明采用簡化計算方法還是相對適用的。

4 結論

采用空心薄壁高墩T形剛構鐵路橋在加速度峰值為0．57g的順橋向兩條罕遇地震波作用下，墩底截面塑性鉸區處于較弱的非線性受力狀態，其受到的損傷較小，具有較好的抗震能力。結構考慮非線性塑性反應后的地震力與彈性相比明顯減小，其中Taft波引起的地震反應比El－Centro波相對要大。墩頂截面均處于未開裂的線彈性工作階段，結構不會有損傷；墩底截面在El－Centro波作用下進入開裂階段末段，未到達屈服階段，但在Taft波作用下進入較弱的屈服塑性工作階段，結構損傷較小，橋墩無破壞現象發生，滿足規范“大震不倒”的要求。且在罕遇地震作用下，墩頂位移較小，非線性位移延性比最大僅為1．362，延性驗算滿足規范要求，在罕遇地震下結構處于有限的非線性塑性狀態，這也充分說明了空心薄壁鐵路高墩的延性抗震能力是有足夠保障的。

［1］ GB50111－2006．鐵路工程抗震設計規范［S］．北京：中國計劃出版社，2006．GB50111－2006．Railway engineering anti－earthquake design specification［S］．Beijing：China Plans to Press，2006．

［2］ 吳小峰，孫啟國，狄杰建，等．抗震分析反應譜法和時程分析法數值仿真比較［J］．西北地震學報，2011，33（03）：275－278．

WU Xiao－feng，SUN Qi－guo，DI Jie－jian．A Numerical Simulation Comparison between Response Spectrum Analysis and Time History Analysis［J］．Northwestern Seismological Journal，2011，33（03）：275－278．

［3］ 薜瑞杰，袁萬城．國內外橋梁延性抗震構造設計比較［J］．工程抗震與加固改造，2009，31（02）：1－8．

XUE Rui－jie，Yuan Wan－cheng．Comparison on Domestic and Overseas Constructional Details for Ductility Seismic Design of Bridge［J］．Earthquake Resistant Engineering and Retrofitting，2009，31（02）：1－8．

［4］ 梁智垚．橋梁高墩位移延性能力計算方法研究［J］．工程抗震與加固改造，2005，27（05）：57－62．

LIANG Zhi－yao．Study on Calculational Methods of Displacement Ductility Capacity of Tall Pier［J］．Earthquake Resistant Engineering and Retrofitting，2005，27（05）：57－62．

［5］ 夏修身，陳興沖，王常峰，等．高墩大跨連續剛構橋抗震性能研究［J］．西北地震學報，2010，32（1）：88－90．

XIA Xiu－shen，CHEN Xing－chong，WANG Chang－feng，et al．Study on Seismic Performance of Tall－pier and Long－span Continuous Rigid－framed Bridge［J］．Northwestern Seismological Journal，2010，32（1）：88－90．

［6］ 胡文源，鄒晉華．時程分析法中有關地震波選取的幾個注意問題［J］．南方冶金學院學報，2003，24（4）：25－28．

HU Wen－yuan，ZOU Jin－hua．Time History Analysis Method for Seismic Wave Selection of A Few Pay Attention to the Problem［J］．Journal of Southern Institute of Metallurgy，2003，24（4）：25－28．