災損曲線的構建及其在巨災保險中的應用

張涵博

巨災保險是巨災風險管理中的重要工具。通過巨災保險，可以將自然災害的損失風險進行有效的分散和轉移，促進防災減災和災后重建工作的開展，對于一國的經濟社會繁榮穩定有著非常重要的作用。我國是一個自然災害頻發的國家，面臨著除了火山爆發之外所有的巨災風險，巨災保險對我國有著尤為重要的意義。

巨災風險有著與常規風險截然不同的特點:從發生頻率來看，常規風險通常發生頻率較高，但巨災風險的發生頻率極低;從損失規模來看，常規風險的損失一般只與單個風險標的的價值有關，而在巨災風險中通常某一地區的所有風險標的都受影響;從空間和時間分布來看，常規風險的發生和分布比較分散，但巨災風險通常會在某一時間、某一地區集中發生，造成高額損失。上述特點使得巨災保險相對于普通保險在產品開發和定價方面有著更大的困難:常規風險的頻發性使得采用大數定律等傳統保險精算方法估計風險損失的波動性較小，而巨災風險的低頻高危性使得傳統方法對風險損失的估計與實際情況可能會有較大出入。要衡量巨災風險的大小，必須通過巨災建模(Catastrophe Modeling)，在經驗數據的基礎上構建巨災損失模型。

災損曲線是反映巨災的損失程度與發生頻率之間關系的曲線，是巨災損失模型的核心組成部分。它可以確定某一損失規模巨災事件的發生頻率，從而求出巨災總損失的數學期望值并實現巨災保險的定價。超概率曲線(Exceedance Probability Curve，EP)是災損曲線的主要形式之一。本文將首先介紹超概率曲線構建的一般原理，進而提出一種在經驗數據的基礎上通過計算機模擬構建巨災超概率曲線的方法，最后將探究超概率曲線在巨災保險中的應用及意義。

一、構建超概率曲線的一般原理

超概率曲線是概率論中進行累積頻率分析(Cumulative Frequency Analysis)的重要工具，它是用圖形表示在給定時期內或給定事件中超過一定損失水平事件的發生概率，通常用縱軸表示概率，橫軸表示損失水平。對于某種災害損失，超概率是指在某段時間內或某些災害事件中，發生大于特定損失規模災害事件的概率。當損失為0時，超過這一損失的概率為1;隨著損失規模的提高，超概率將隨之下降。

一般而言，在構建超概率曲線時，服從以下一些基本假設:

1.有一系列自然災害損失事件Ei;

2.對于每起事件，都有發生概率pi和對應的損失Li;

3.某一年中災害發生的次數并不局限于一次，可以是多次;

4.所有災害事件都是相互獨立的，服從 Bernoulli分布，即對于任意的m和n，都有P(Em/En)=P(Em)，每起災害損失事件的發生時間、發生頻率、損失程度等參數都不受其他災害損失事件發生與否的影響。

在以上假設下，每一起災害損失事件Ei都是一個獨立隨機變量，其概率分布函數定義如下。

P(Ei發生)=pi

P(Ei不發生)=(1－pi)

若災害不發生，則損失為零。所以某年中某一災害事件Ei的期望損失為:

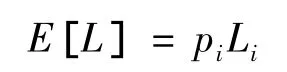
如果我們用AAL(Average Annual Loss)來表示所有災害事件在一年中的總期望損失，則其表達式為:

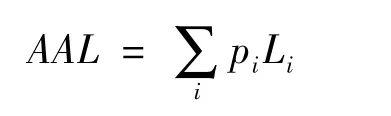
假設某一年中只發生了一次災害事件，則某一損失水平的超概率EP(Li)，即超過該損失水平的災害損失事件的發生概率，就相當于1減去這一年中所有低于該損失水平的災害事件都沒有發生的概率。它可以由以下式子求得:

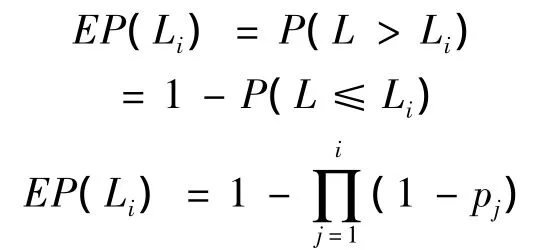
將相應的損失額度Li和相應的EP(Li)繪制在圖上，即可得到這一年中巨災損失的超概率曲線，如下圖:

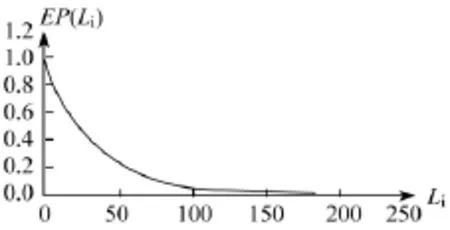
圖:超概率曲線示例圖

在圖中，橫軸Li表示損失水平(橫軸上的數字是假設的損失值)，縱軸EP(Li)表示其所對應的超概率。在損失水平為0時，所有損失事件的損失額度都會超過0，此時對應的超概率是1。一般而言，隨著損失水平的提高，相應的超概率也越來越低，但其下降幅度將逐步減緩。即超概率曲線滿足以下性質:

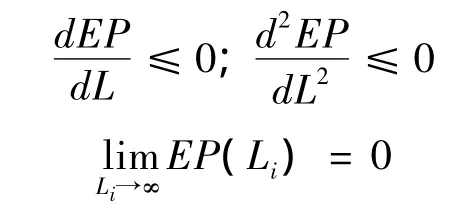
二、通過計算機模擬構建年度巨災損失超概率曲線

在以上基本原理中，若要構建年度災害損失超概率曲線并求得AAL，必須能夠確定在某一年中，某一特定的災害損失事件Ei發生的確切概率 pi。理論上，pi可以通過統計多年的經驗數據獲得。但在實際中，一方面，由于我國巨災監控體系是在建國之后才逐步建立和完善的，歷史數據并不全面;另一方面，改革開放后經濟社會快速發展使得經濟體制轉型前后的災害損失數據缺乏可比性，因此中國巨災損失歷史數據非常有限，通過簡單統計這些數據得到的pi并不準確。在構建超概率曲線時應當借助計算機生成虛擬的災害事件來模擬災害的損失情況，以彌補歷史數據的不足。本部分將提出一種在經驗數據的基礎上通過計算機模擬構建年度巨災損失超概率曲線的方法。首先根據歷史數據得到單起災害事件中損失的分布情況，然后建立每年某種巨災事件發生次數的分布，最后由計算機模擬年度災害損失情況以構建年度巨災損失超概率曲線。

第一步:建立單起災害事件損失分布

一般而言，對于地震、臺風這樣的自然災害，我國每年都會發生數十次，在二十年的時間里能夠積累到數百個有效的災害損失數據。如果這些災害事件的損失都服從同樣的分布，數百起事件已經足以構成大樣本，通過統計這些數據就能找到單起災害事件的損失分布。在第一步中，我們把某種自然災害的總體看成一個隨機變量，把所收集的該種災害損失事件看作是巨災損失總體的樣本。在構建單起災害事件損失分布時接受以下假設:

1.收集的每起該種災害損失事件Ei都是該種災害損失隨機變量ξ的一個樣本，且樣本容量足夠大;

2.所有災害損失事件Ei都服從同樣的分布;

3.所有災害損失事件Ei都是相互獨立的;

4.在每一起災害損失事件中，對于某一可能的損失水平Li，有對應的損失概率pi。

在以上假設下，某一時間段內我國所有的該種災害損失事件相當于在同樣條件下重復進行的數百次實驗，構成了一個獨立試驗序列概型。由于每次試驗的結果Ei與其他各次試驗結果無關，因此這一系列重復實驗構成了n重Bernoulli實驗。

由于假設所有災害損失是一個隨機變量總體ξ，可以設(x1，x2，…xn，)是總體 ξ的樣本 Ei的觀察值，即每起災害損失事件中的經濟損失數額。將它們按大小排列為，令

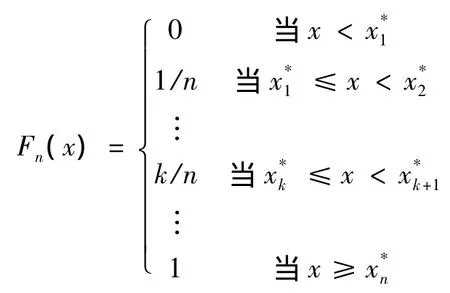
則Fn(x)的圖形就構成了累積頻率曲線。它是跳躍式上升的一條階梯曲線。若觀測值不重復，則每一躍度為1/n;若觀測值有重復，則按照1/n的倍數跳躍上升。

根據Bernoulli大數定律，在獨立試驗序列中，當試驗次數n無限增加時，事件A的頻率k/n(k是n次試驗中事件A發生的次數)，收斂于它的概率P(A)=p。即，對于任意給定的ε＞0，有

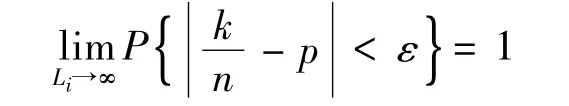
也就是說，當試驗在不變的條件下重復進行很多次時，隨機事件的頻率在它的概率附近擺動，并將隨著實驗次數的增加而不斷趨近其概率。在樣本的累積頻率曲線Fn(x)中，對于任何實數x，Fn(x)等于樣本的n個觀察值中不超過x的個數除以樣本容量n，因此Fn(x)可以作為未知的整體ξ的分布函數Fξ(x)的一個近似。樣本容量n越大，近似得越好。在數百起災害損失事件的大樣本下，可以近似地認為樣本累積頻率曲線Fn(x)等同于災害損失整體分布曲線Fξ(x)。由于Fn(x)實質上是所有低于某一損失水平x的災害事件發生的概率，因此用1－Fn(x)可得出所有高于x的災害損失事件的發生概率，即單起災害損失的超概率曲線。

需要說明的是，并不是所有的災害損失數據都能夠符合前提假設:

第一，對于最重要的“同分布”假設，災害損失的原始數據很可能無法滿足:隨著經濟社會的發展，一個地區的財富積累會越來越多。在其他條件不變的情況下，同樣破壞程度的災害事件造成的損失將逐步擴大。再加上通貨膨脹因素，嚴格來說，在長時間跨度中，災害損失并不符合同分布假設。在這種情況下應對損失數據進行一定的處理，以消除通貨膨脹或經濟增長等外部因素的影響。

第二，自然災害的特點可能使得“獨立”這一假設在現實中不一定成立。同一類型的不同災害事件之間，以及不同類型的不同災害事件之間，的確可能存在一定的因果關系，并不一定是完全獨立的。由于科學界對自然災害的形成和相互作用機理仍未充分研究，因此只能暫時假定所有災害事件都是相互獨立的。

第三，某些自然災害的發生頻率較低，難以滿足“樣本容量足夠大”的假設。在我國，海嘯、火山爆發發生的可能性微乎其微，由于樣本容量太小，無法通過上述方法來找出這兩種自然災害的損失分布情況。

此外，對于一些極端損失事件，在必要時應當作為極端值舍棄。如汶川地震，其損失占2008年當年地震直接經濟損失的99.16%，占 1990～2008年中國地震總損失的90%以上，遠超出其他地震的損失規模(鄭通彥，2009)。極端大的損失對應著非常小的概率，為了維持數據的可處理性，根據小概率事件的實際不可能性原理，在構建地震的單起災害損失分布時應當去除汶川地震這樣的極端事件。

經過以上數據處理后可建立單起災害事件損失分布模型。通過它可以得到在每起災害事件中，損失水平超過Li的概率EP(Li)，由此構建單起災害損失事件超概率曲線。

第二步:構建年度災害發生次數分布模型

與構建單起災害損失分布模型的假設類似，我們假定每年某種災害的發生次數也是相互獨立并服從同一分布的。一般而言，每年某種自然災害(如地震、臺風、洪水等)的發生次數往往呈現出圍繞著平均值上下波動的現象。如果有相當長的年度災害發生次數數據(如20年左右)，可以驗證其是否服從正態分布。

首先，繪出年度災害發生次數數據的分布直方圖，并求出其峰度與偏度。如果直方圖呈現出正態分布的形態，并且這些數據的峰度和偏度趨近正態分布的特征(峰度為3，偏度為0)，則可以近似地認為年度災害發生次數數據基本符合正態分布。

為了進一步檢驗樣本數據是否服從正態分布，可以通過統計軟件來進行相關檢驗:通過Eviews軟件可以求出樣本數據的Jarque－Bera統計量，通過 SAS或SPSS軟件也可以求出樣本數據的Shapiro－Wilk或Kolmogorov－Smirnov統計量。如果統計量的值大于0.05，則接受檢驗原假設，即樣本數據服從正態分布。

若樣本數據的期望為μ，標準差為σ，樣本數據具有較大的樣本容量，符合正態分布的特征，且能夠通過正態分布的相關檢驗，則可近似地認為年度災害發生次數分布服從期望為μ、標準差為σ的正態分布。

第三步:通過計算機模擬構建年度災害損失超概率曲線

在前面兩步中，我們分別建立了單起災害損失分布和年度災害發生次數分布。接下來，通過計算機隨機抽取每年災害發生次數和每次災害損失，經過大量的抽取模擬后(如1000年)，可以得到長時間段的年度災害損失狀況，以此可構建年度災害損失分布曲線。

在構建某種年度災害損失超概率曲線時，我們假設:1.任意一起災害的損失都服從第一步中得到的單起災害事件損失分布;2.任意一年中某種災害發生次數都服從第二步中得到的年度災害發生次數分布，即期望為μ、標準差為σ的正態分布。

在以上假設下，采用以下算法模擬某種災害年度損失總額:

步驟一，根據年度災害發生次數分布生成第i年災害發生次數ni;

步驟二，根據單起災害事件損失分布生成ni次災害損失事件，每次分別有kij的損失，構成第i年中的災害損失序列;

步驟三，將這ni次災害事件的損失加總，構成第i年的災害損失總額

步驟四，將步驟一至步驟三重復m次，得到m年中每年的年度災害損失總額序列:K1，K2，…，Ki…，Km－1，Km。

最后，采用第一步中的方法，使用這m個模擬的年度災害損失總額構建它們的分布模型，就得到了年度災害損失超概率曲線。在計算機的輔助下可以模擬出數千年的年度災害損失情況，由此得到的超概率曲線比簡單通過幾十年的災害損失記錄得到的超概率曲線更加準確。

三、災損曲線在巨災保險中的應用

以超概率曲線為代表的災損曲線確立了災害損失的大小與發生概率之間的關系，是巨災保險費率厘定、風險評估、承保決策及風險轉移過程中必不可少的重要工具。在前文構建的超概率曲線的基礎上，本部分將探究災損曲線在巨災保險中的應用。

第一，災損曲線為巨災保險的費率厘定提供了依據。在厘定保險的純保費時，需要滿足的基本條件是收取保費的現值應等同于損失賠付期望的現值。由于災害事件發生頻率低，通過歷史經驗數據很難準確估計出未來損失的期望。以美國1994年北嶺地震為例，在地震前美國地震保險的低費率(每千美元保額的保費約為2美元)導致北嶺地震造成的125億美元巨額保險索賠，超過了此前20年間美國保險公司所收取的地震保險保費總和(朱文杰，2006)，因此合理的費率對巨災保險至關重要。在建立合適的災損曲線后，保險公司能夠掌握災害損失大小與發生概率之間的關系，通過計算出年度總期望損失(AAL)而得到的巨災保險費率將更加符合實際情況。

第二，災損曲線使保險公司能夠較準確地評估其所承保的巨災風險的規模。保險公司對于災害賠付的承受能力是有一定限度的，為了確保公司經營的穩定性和連續性，對承保風險的評估非常必要。根據超概率曲線可以得到一定損失規模災害事件的重現周期，從而評估巨災風險的大小。在超概率曲線示例圖中，損失為100的災害事件對應的超概率約為0.052，這意味著損失規模超過100的災害事件的重現周期是1÷0.052≈19.2 年。如果一家保險公司設定其所能接受的最大風險是重現期為50年的災害事件，即 EP=0.02，那么根據超概率曲線示例圖，在該巨災保險中最大可能損失約為132。

第三，災損曲線可以為保險公司巨災保險的承保決策提供依據。為了確保安全穩健經營，保險公司會盡量避免出現償付能力不足的情況。假如一家保險公司可以接受償付能力不足情況的最大出現概率是p0，用L代表賠付損失，n代表承保保單的數量，a代表每份保單收取的保費，S代表現有盈余，那么保險公司經營的約束條件是:

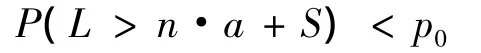
在超概率曲線中，根據EP=p0可以求出對應的L。若保險公司的保費收入與盈余之和無法達到L，那么此時就無法滿足以上約束條件，繼續承保該巨災保險會使公司面臨償付能力不足的風險。

第四，災損曲線可用于巨災風險轉移決策。巨災風險具有發生頻率低、損失規模大、較易集中發生的特點，單一一家保險公司往往無法單獨承受巨災保險的巨額賠付。承保巨災保險的保險人可選擇再保險或巨災債券等風險轉移措施，以進一步分散巨災風險并減少需要持有的自有資本，但需支付再保費或債券利息而降低保險公司的預期收益。為了在保證償付能力的前提下實現收益最大化，保險公司必須維持自留風險和分出風險的平衡。在評估巨災風險轉移措施時，災損曲線具有以下作用:一方面，通過災損曲線，原保險人和再保險人可以計算自留風險和分出風險的期望賠付，進而確定再保險的保費或巨災債券的利息;另一方面，保險人可以通過災損曲線計算出在滿足償付能力約束條件時自身所能承受的最大風險，進而決定分出額的大小。因此，災損曲線可以幫助保險公司做出合適的巨災風險轉移決策。

總體而言，災損曲線作為巨災模型的核心組成部分，是評估巨災風險規模的重要工具，對巨災保險的產品開發、運營管理有著決定性的作用。應用計算機模擬使得災損曲線能夠擺脫歷史數據不足帶來的困擾，增強了災損曲線的準確性，并使得巨災保險的定價和保險公司的決策更加合理。