工程項目估價概率分析

周建國，徐寧，楊正凱

(1.山東建筑大學 管理工程學院，山東 濟南 250101;2.山東建筑大學 理學院，山東 濟南 250101;3.山東建筑大學土木工程學院，山東 濟南 250101)

0 引言

在項目策劃及實施的各個階段，都要進行工程估價。現行的工程估價方法是根據建筑產品在建造過程中所發生的費用，以施工過程為依據，計算工程數量及單價，或套用定額(估算、概算、預算定額)，按照取費標準計算得到的是一個固定值。建筑產品在生產過程中受各種因素的影響，如企業勞動生產率的高低、原材料的消耗量及價格變動、機械設備的利用程度、項目管理水平、以及現場條件的變化和工程合同條款的不同、市場競爭程度等[1]。由于這些不可控因素的影響，在預計工期內，工程項目有些費用是隨機的，存在著多種變化狀態(或范圍)，很難精確的進行估算[2－3]。準確的工程估價，對項目發起組織和設計團隊都是非常重要的[4－6]。不準確的估價，必然會增加項目的風險[7－8]。國內外概率的應用研究主要集中在工程的評價、決策、極限狀態評估等領域，如風險(安全)評價、計劃評審技術PERT(Program Evaluation and Review Technique)及可靠性評估等方面，而應用在工程估價方面，尚缺少系統的研究。文章擬將概率分析的概念引入到工程估價中，驗證單項工程估價偏差或誤差分布近似服從β分布，單項估價的累加平均值近似服從正態分布，可以應用中心極限定理為項目估價給出一個概率范圍，從而為項目的決策和風險評估提供有價值的信息。

1 工程項目估價原理及程序

1.1 項目估價值概率分布的確定

建設工程項目的計價是一個復雜過程，其基于通用的環境和條件、正常的執行情況。因為確定項目估值的因素，如材料設備的價格，工資、利率、匯率等是不斷變化的，這些變化影響了建設工程費用估價的準確性，將這些影響定義為偏差或誤差，這些偏差或誤差決定了項目估價的不確定性[8－10]。

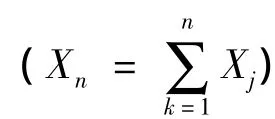
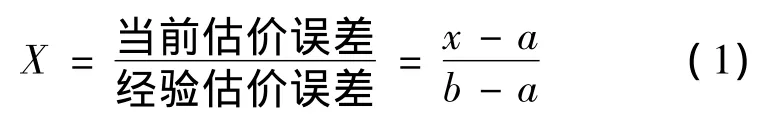
式中:x為當前估價;a為經驗估價最小值;b為經驗估價最大值。

則X具有下列三個特征:(1)X在0，1之間;(2)X的取值具有隨機性;(3)X與1－X在幾何上具有對稱性。具有這些特征的隨機變量可看作服從或近似服從β分布。即X的密度函數如下

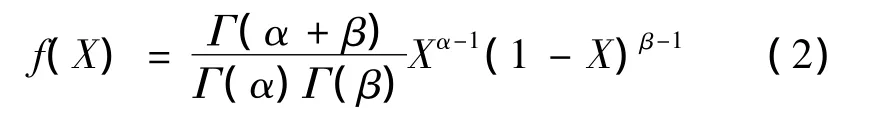
通過β分布計算隨機變量的均值和方差十分方便。估算出隨機變量X的均值后，我們可推出當前估價x的均值與方差。

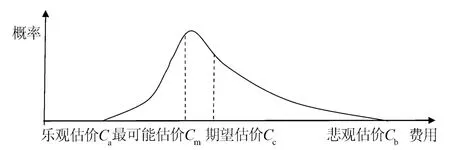
圖1 β分布曲線

假設分項工程x有一個有限的樂觀估價x1、悲觀估價x2以及最可能估價xm，則對應相對誤差有樂觀誤差x1、悲觀誤差x2和最大可能誤差xm。這三個值是主觀估計值，根據它們可推算出相對誤差X的均值與方差，并推算出估價X的均值(μX)與方差(σ2)。

注意:當a≤x1≤b、a≤x2≤b時，經常地用a、b 分別表示 x1、x2。

1.2 項目估價概率分布規律分析

工程項目的估價是由大量的項目活動發生的費用累加得出的，其中每一個項目活動費用在總費用中所起的作用都是微小的，沒有一項因素起特別突出的影響，項目的總費用受多個隨機因素的影響，這種隨機變量往往近似地服從正態分布。在項目費用的確定過程中，我們往往只關心項目的總費用，而不關心個別因素的作用，為了評估項目費用的不確定性，可以用中心極限定理來描述隨機變量和的概率分布規律，即在一般情況下，大量隨機變量的平均值近似服從正態分布[11]，因此可以應用正態分布對項目費用發生情況作近似分析。

假設某項目要進行投資決策，共有n個分項項目，構成隨機變量序列C1，C2，…Cn其相互獨立，服從同一分布，由上一步分析知:

注意到等式(7)的右端是標準正態分布的分布函數。即當n充分大時(n＞15)，獨立同一分布的n個隨機變量C1，C2，…Cn之和近似地服從正態分布 N(nμ，nσ2)。

1.3 項目估價概率分析計算程序

1.3.1 根據已知計劃費用確定項目可完成的概率

(1)確定估價項目，并對每一項目進行樂觀、悲觀和最可能性估價分析。

(2)求每一估價項目的均值和方差。即求出

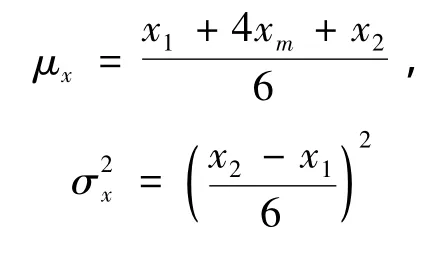
(3)確定項目總費用值的均值。

(4)計算項目費用的標準偏差:

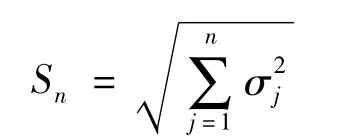
(5)用標準偏差確定標準正態曲線的橫坐標值Z，即

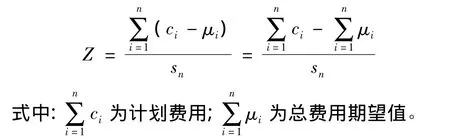
1.3.2 根據項目費用控制要求的控制可靠性概率，確定期望費用

用上例相似的方法，根據已知概率可求出期望費用。

2 工程項目估價概率實例分析

某大型國際機場項目，計劃投資額為89.4億元，建設方在投資決策前，需要做一個針對項目投資合理性的經濟分析，確定能夠按此投資額完成建設的把握。

(1)確定估價項目并進行三值估計

根據項目設計，項目共由86項估價項目組成，為了得到項目按計劃投資額完成的概率，成立了一個由多位估價專家組成的專家組，為項目活動給出了樂觀、悲觀及最可能投資估計值(如表1所示)。

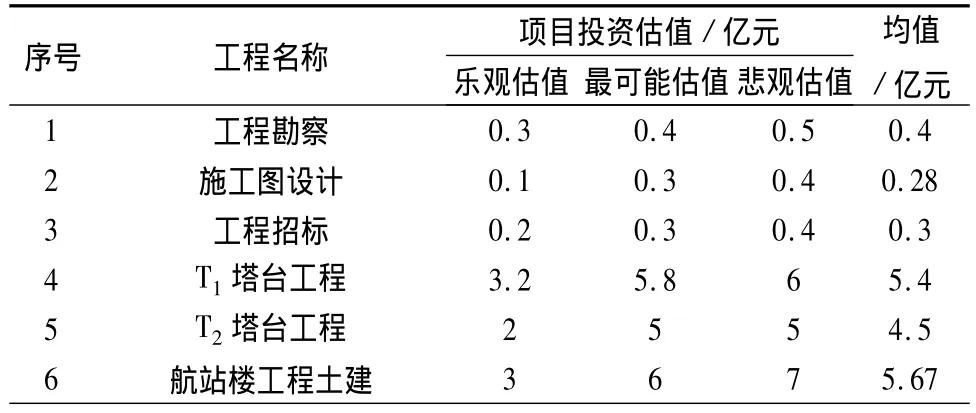
表1 項目估值表

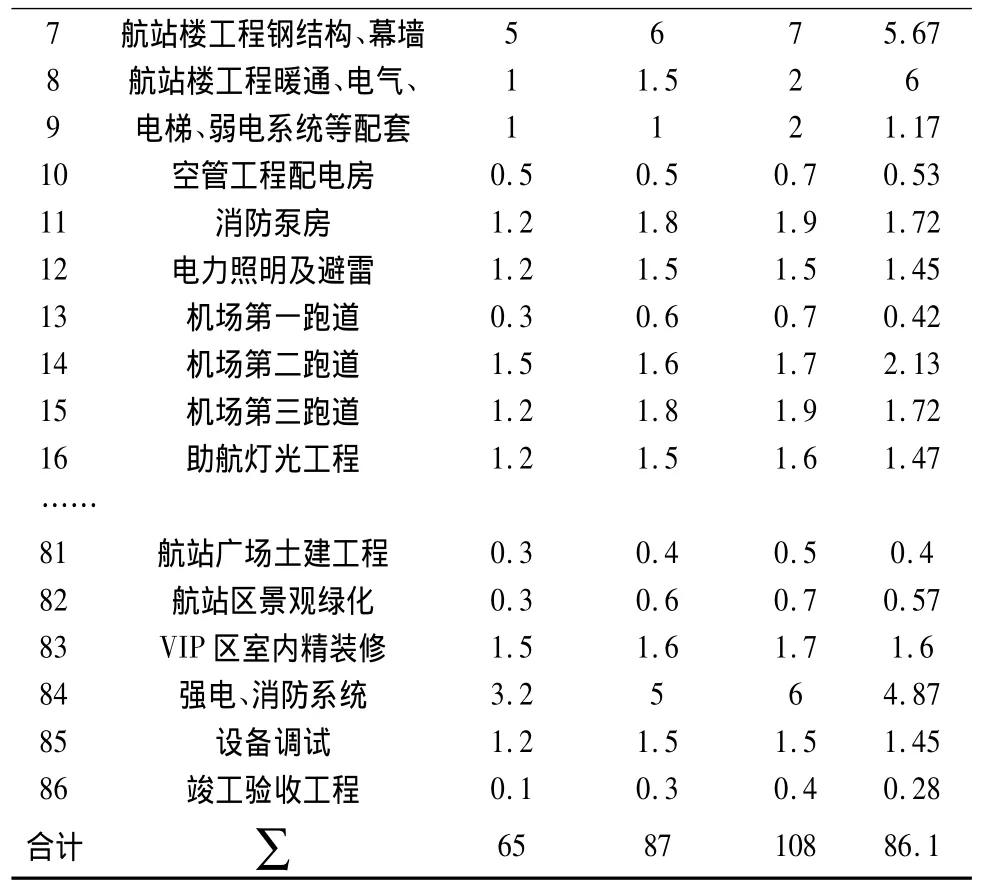
續表1:

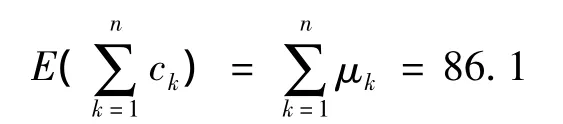
(3)計算項目估值方差及正態分布的標準偏差

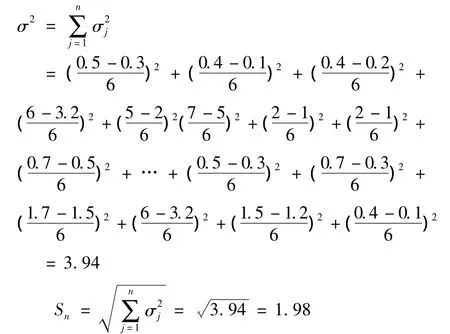
(2)確定工程投資的總平均估值

由公式(3)及表1確定工程投資的總平均估值

(4)用標準差確定正態曲線橫坐標值

(5)確定項目期望投資額完成概率

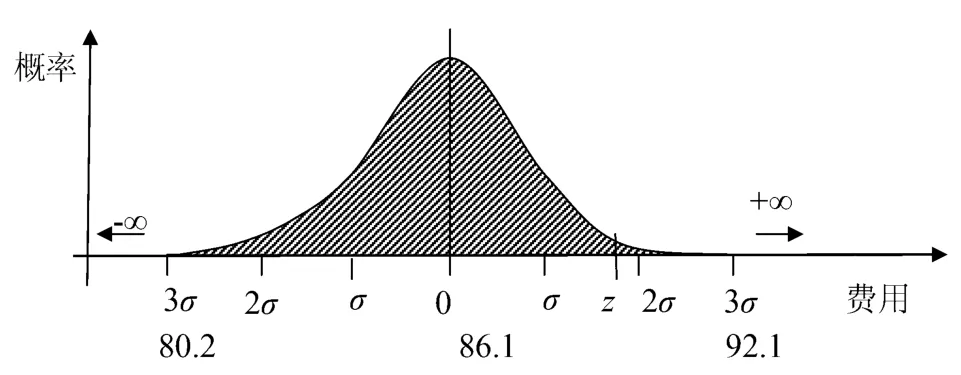
圖2 正態分布曲線

即有95%的置信度，保證工程在計劃投資額89.4億元內完成。

3 結論

工程項目的建設是一個復雜和有較長建設周期的過程，在項目建設的不同階段需要做出相應的項目估算(設計概算、施工圖預算及竣工結算等)，估算的精度取決于項目已知的信息量，估算的誤差最大可能會達到+50%到－30%的范圍。研究將概率分析的方法應用到工程估價中，驗證了(1)每一項工程的估價都是大量隨機變量的疊加，這些隨機變量的平均值近似服從正態分布，可以應用中心極限定理來描述其分布規律;(2)應用概率分析做出的項目估價，可以給出估價值的置信度及置信區間或估價值的浮動范圍;(3)此估價方法在估價項目數量較大(＞15)時結論才為有效。

[1]陳建國.工程計量與造價管理[M].上海:同濟大學出版社，2001.

[2]陳勝群.現代成本管理理論[M].北京:中國人民大學出版社，1998.

[3]王槐林.采購管理與庫存控制[M].北京:中國物資出版社，2012.

[4]邢莉燕，邵朝紅.云視角下的工程造價風險評價[J].山東建筑大學學報，2010，25(4):429 －433.

[5]鄧培林，袁建新.基于招投標博弈報價策略分析[J].數學的實踐與認識，2011(12):78－80.

[6]邢亞倩.基于資金時間價值的投標決策過程的資源優化[J].西南交通大學學報，2012(6):45－47.

[7]徐立新，張新成，吳相林.基于數理統計的工程投標決策定量分析方法及應用[J].計算機工程與應用，2006(08):46－47.

[8]Ellram L.M.A..Managerial guideline for the development and implementation of purchasing partnerships[J].Intemational Joumal of Purchasing and Materials Management，1991，27(3):2 －8.

[9]Landeros R.R.，Plank R.E..Maintaining buyer supplier patner ships[J].International Goumal of Purchasing and Materials Management，1990，31(3):3 －31.

[10]王雪青，張帆.基于DEA－Tobit的建筑業企業效率研究[J].山東建筑大學學報，2011，26(4):343 －347.

[11]楊永發.概率論與數理統計教程[M].天津:南開大學出版社，2000.

[12]趙道致，張文慧.招投標中的激勵機制設計[J].現代財經－天津財經學院學報，2002(11):28－30.