動態規劃的應用
劉鳳鳴
(浙江海洋學院 數理與信息學院,浙江 舟山 316000)
1 動態規劃的基本概念
多階段決策過程,是指一類特殊的過程,它們可以按時間順序分解成若干個相互聯系的階段,稱為“時段”,在每個時段都要做決策,全部過程的決策是一個決策序列。多階段決策問題也稱為序貫決策問題。
多階段決策問題的目標是要達到整個活動過程的總體最優。在每個階段進行決策時不應僅考慮本階段最優,尤其應考慮對最終目標的影響,從而做出對全局來說最優的決策。動態規劃是符合這種要求的一種決策方法。
動態規劃開始只是應用于多階段決策性問題,后來漸漸被發展為解決離散最優化問題的有效手段,進一步應用于一些連續性問題上。然而,動態規劃更像是一種思想而非算法,它沒有固定的數學模型,沒有固定的實現方法,其正確性也缺乏嚴格的理論證明。因此,一直以來動態規劃的數學理論模型是一個研究的熱點。一個多階段決策過程最優化問題的動態規劃模型通常包含以下基本要素:階段、狀態、決策、策略、狀態轉移方程、指標函數和最優值函數,在建立動態規劃數學模型時,主要是確定這些動態規劃的基本要素。
2 動態規劃算法的基本步驟
2.1 劃分階段
應將實際問題恰當地分割成n個子問題(n個階段)。通常是根據時間或空間而劃分的,或者在經由靜態的數學規劃模型轉換為動態規劃模型時,常取靜態規劃中變量的個數n,即k=n。
2.2 選擇狀態
正確地定義狀態變量sk,使它既能正確地描述過程的狀態,又能滿足無后效性.動態規劃中的狀態與一般控制系統中和通常所說的狀態的概念是有所不同的。
2.3 確定決策并寫出狀態轉移方程
之所以把這兩步放在一起,是因為決策和狀態轉移有著天然的聯系,狀態轉移就是根據上一階段的狀態和決策來導出本階段的狀態。所以,如果我們確定了決策,狀態轉移方程也就寫出來了。但事實上,我們常常是反過來做,根據相鄰兩段的各狀態之間的關系來確定決策。
2.4 寫出規劃方程(包括邊界條件)
動態規劃的基本方程是規劃方程的通用形式化表達式。一般說來,只要階段、狀態、決策和狀態轉移確定了,這一步還是比較簡單的。
3 動態規劃應用問題
3.1 資源分配問題
例:某物流公司每天要給3家公司運送6車貨物,如果各公司獲得這些貨物之后獲得的盈利如表1所示,則這車貨物如何分配給各工廠才能使盈利最大。
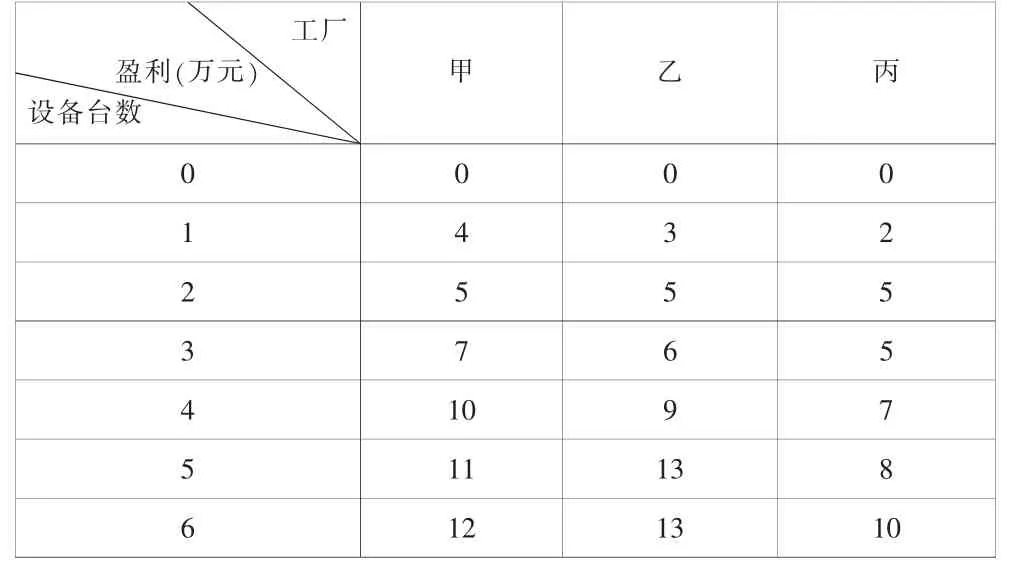
表1
解:將問題按公司分為3個階段,甲、乙、丙三個公司分別編號為1、2、3
設sk表示為分配給第k個公司至第n個公司的貨物車數
xk表示為分配給第k個公司的貨物數量
則sk+1=sk-xk為分配給第k+1個公司至第n個公司的貨物車數
pk(xk)表示為xk車貨物分配到第k個公司所得的盈利值
fk(sk)表示為sk車貨物分配給第k個公司至第n個公司時所得到的最大盈利值
根據逆推關系式
fk(sk)=max{pk(xk)+fk+1(sk-xk)},k=3,2,1
0≤xk≤sk
f4(s4)=0
所以從最后一個階段開始向前逆推計算
第三階段:
設將 s3 車貨物(s3=0,1,2,3,4,5,6)全部分配給公司丙時,最大盈利值為
f3(s3)=max[p3(x3)]
其中 x3=s3=0,1,2,3,4,5,6
因為此時只有一個公司,有多少車貨物就全部分配給公司丙,故它的盈利值就是該段的最大盈利值,其數值計算如表2所示。
第二階段:
k=2 時,設把 s2 車貨物(s2=0,1,2,3,4,5,6)分配給公司乙和丙時,對每個s2值有一種最優分配方案,使最大盈利值為

表2
表中,x3*表示使f3(x3)為最大值時的最優決策。
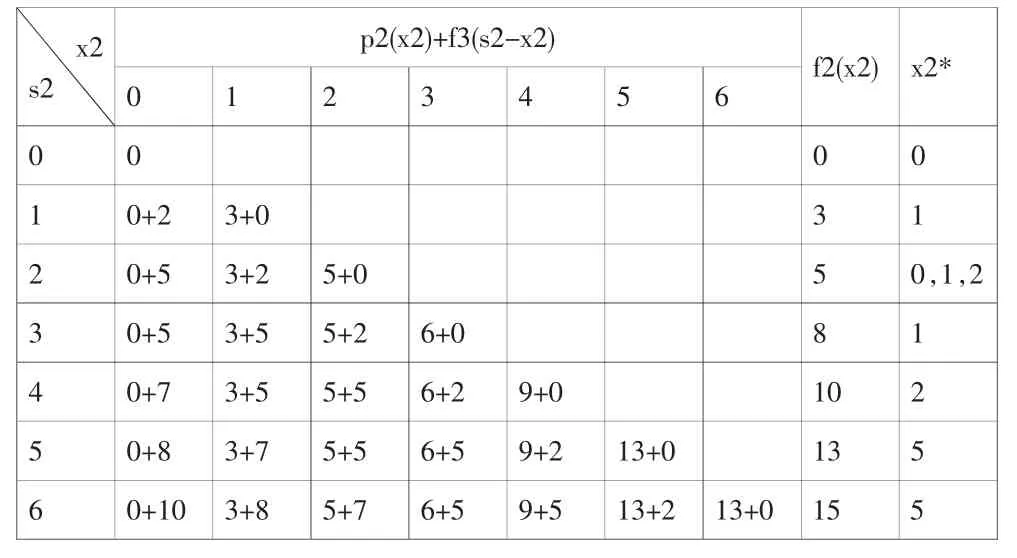
表3
f2(s2)=max[p2(x2)+f3(s2-x2)]
其中 s2=0,1,2,3,4,5,6
因為乙公司x2車,其盈利為p2(x2),余下的s2-x2車就給丙公司,則它的盈利最大值為 f3(s2-x2)。 現在選擇x2的值,使 p2(x2)+f3(s2-x2)取最大值,其數值計算如表3所示。
第一階段:
k=1時,設把s1車(這里只有s1=6的情況)貨物分配給甲、乙、丙三個公司時,最大盈利值為
f1(6)=max[p1(x1)+f2(6-x1)]
其中 x1=0,1,2,3,4,5,6
因為給甲公司x1車,其盈利為p1(x1),剩下的6-x1車就分給乙和丙兩個公司,則它的盈利最大值為f2(6-x1),現選擇 x1值,使p1(x1)+f2(6-x1)取最大值,它就是所求的總盈利最大值,其數值計算如表4所示。

表4
根據計算表格的順序反推算,可知最優分配方案為:
x1*=1,由于s2=s1-x1*=6-1=5,查第二個表可知x2*=5,s3=s2-x2*=5-5=0
即得甲公司分配1車,乙公司分配5車,丙公司不分配,總盈利為17。
3.2 設備更新問題
現以一臺機器設備為例,在使用過程中,每年都面臨繼續使用或更新的決策,要求在n年內的每年年初作出決策,是繼續使用舊設備還是更換一臺新的,使n年內總效益最大。
n為設備計劃使用年數。
Ik(t)為第k年(階段)機器役齡為t年的一臺機器運行(在使用一年)所得的收入。
Ok(t)為第k年機器役齡為t年的一臺機器運行(再使用一年)時所需運行的費用(或維修費用)。
Ck(t)為第k年機器役齡為t年的一臺機器更新時所需的凈費用(處理一臺役齡為t的舊設備,買進一臺新設備的更新凈費用)。
a為折扣因子,表示一年以后的收入是上一年的a單位。
T為在第一年開始正在使用的機器的役齡。
最優指標函數gk(t):表示第k年初,使用一臺已用了t年的設備,到第n年末的最大收益。
xk(t)表示給出 gk(t)時,在第 k 年開始時的決策(保留或更新)建立動態規劃模型如下:
階段k(k=1,2,…,n)表示計劃使用該設備的年限數。
決策變量xk:是第k年初更新,還是保留使用舊設備,分別用R,K表示。
狀態轉移方程為:
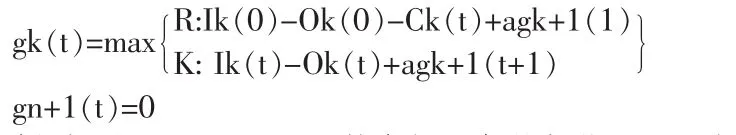
例:假設n=5,a=1,T=1,某臺新設備的年收入及運行費用、更新費用如表5,試確定五年內的更新策略,使總效益達到最大。
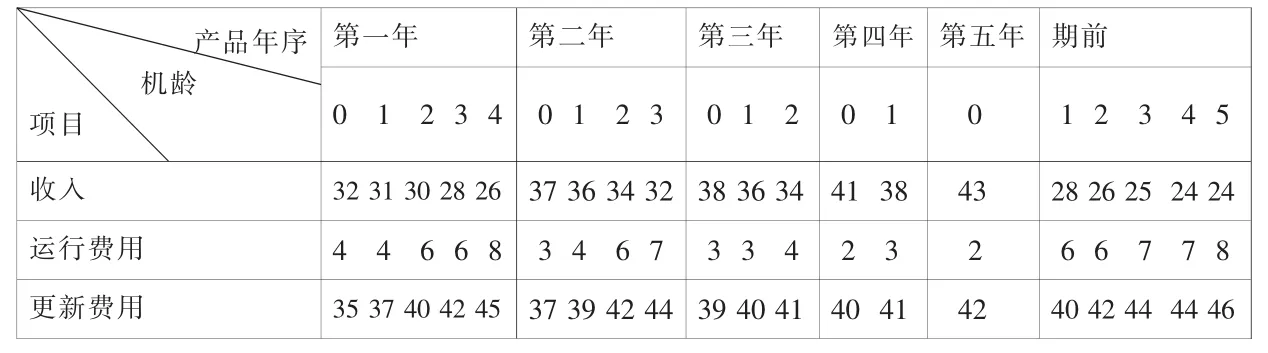
表5
解:因第k年開始機齡為t年的機器,其制造年序應為k-t年,因此,I5(0)為第五年新產品的收入,即 I5(0)=43,I3(2)為第一年的產品其機齡為 2年的收入,即I3(2)=30,C5(1)是第五年機齡為1年的機器(應為第四年的產品)的更新費用,即C5(1)=41,其余同理類推。
當k=1時,由于設T=1,所以從第五年開始計算時,機器使用了1、2、3、4、5 年,根據遞推關系式

最后根據上面的結果反推之,可求得最優策略為
第一年機齡為1,最佳策略為K
第二年機齡為2,最佳策略為R
第三年機齡為1,最佳策略為K
第四年機齡為2,最佳策略為K
第五年機齡為3,最佳策略為K
最大收益為99。
4 總結
動態規劃是一種將問題實例分解為更小的、相似的子問題,并存儲子問題的解而避免計算重復的子問題,以解決最優化問題的算法策略。該方法主要應用于最優化問題,這類問題會有多種可能的解,每個解都有一個值,而動態規劃找出其中最優(最大或最小)值的解。若存在若干個取最優值的解的話,它只取其中的一個。在求解過程中,該方法也是通過求解局部子問題的解達到全局最優解,在動態規劃的設計過程中,階段的劃分和狀態的表示是非常重要的兩步,這兩步會直接影響該問題的計算復雜性,有時候階段劃分或狀態表示的不合理還會使得動態規劃法不適用。動態規劃的優點是最優解是全局最優解,能得到一系列(包括子過程)的最優解,不需要對系統狀態轉移方程、階段效應函數等的解析性質作任何假設。缺點是沒有統一的標準模型和標準的算法可供使用,應用有局限性。
[1]運籌學[M].3版.清華大學出版社
[2]動態規劃案例[OL].百度文庫.
[3]運籌學動態規劃[OL].百度文庫.

