多平臺傳感器跟蹤系統無序量測濾波器設計

張 舉（中國電子科技集團公司 第二十研究所，陜西 西安710068）

0 引言

現代海戰中，超低空突防的來襲導彈已構水面艦艇的主要威脅，而單平臺的偵察探測能力不能滿足反導作戰的要求，在此背景下，充分利用多平臺傳感器的信息共享可以提高其反導效果。當采用多平臺傳感器探測的數據進行融合時，由于不同類型的傳感器的采樣率、預處理時間以及數據通信延遲，導致出現多個傳感器量測無序到達融合中心的現象[1]，即無序量測現象。由于Kalman濾波算法只適于處理順序量測，因此基于Kalman濾波框架的量測融合算法不能直接處理狀態估計的負時間更新問題。當前針對無序量測現象的濾波方法主要有：丟棄延遲量測法、重新濾波法、數據緩存法和直接更新法[2]。丟棄延遲量測法會造成大量信息丟失，導致目標跟蹤精度下降甚至丟失目標。對于重新濾波法，存儲量和計算量隨傳感器數目、目標數目及延遲時間的增長而顯著增加。數據緩存法需要較大的存儲空間而且輸出嚴重滯后。直接更新法直接使用無序量測更新當前時刻的狀態估計，使其達到或逼近量測順序處理時的濾波精度[3][4]。

1 問題描述

對于協同作戰的多平臺系統，每個協同單元在自身坐標系下進行目標跟蹤的同時，接收其它平臺周期性發送探測信息。

狀態方程和測量方程如下：

其中，ωk～N（0，Qk）為建模誤差，vk～N（0，Rk）為測量誤差。 矩陣 Fk為狀態變換矩陣，Gk誤差輸入矩陣，Xk包含目標位置、速度和加速度。

線性測量方程可通過對非線性觀測函數線性化：

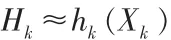
其中，Xk＝［xkykzkx˙ky˙kz˙k］T

對于擴展卡爾曼濾波器的濾波方程如下：

下面在時間軸下，給出采用離散時間擴展卡爾曼濾波的負時間更新的情況。如圖1，用tk-2時刻的測量數據Zk-2，得到標準濾波器推導狀態估計值Xk-2/k-2。tk-1時刻遙控傳感器獲得測量值Zk-1，把這些數據添加時戳tk-1，并提交數據到具有傳輸延時的網上。tk時刻測量值Zk準時到達，并更新狀態估計由Xk-2/k-2得到Xk/k。由于數據延時，測量值Zk-1在tk+時刻到達，把該延遲數據考慮進去用于提高狀態估計Xk/k+。

圖1 負時間更新時間軸

基于上述問題表述的負時間更新算法推導如下：

2 濾波模型推導

2.1 狀態推導

時間間隔表示為：

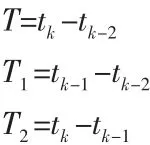
狀態Xk|j估計誤差表示為，相應真值表示為狀態Xk，則

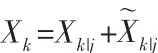
時間間隔T內，狀態Xk∈Rn的離散時間推導表示為：

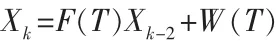
其中，F是離散時間狀態轉換矩陣，W（T）是對象噪聲影響的矢量Xk＝［xkx˙k］T表達式，假定狀態矢量 是一維向量，那么狀態變換矩陣為：

該模型的對象噪聲將為連續時間白噪聲加速度。單位脈沖加速度δ（t-α），tk-2＜α＜tk，將在在狀態空間［tk-2-α 1］T產生響應。 白噪聲加速度ω（α）應用整個時間間隔T產生對象噪聲：

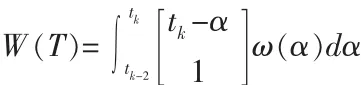
從tk-2到tk狀態估計協方差的時間映射為：

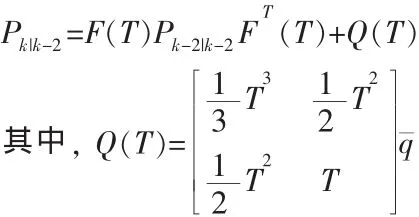
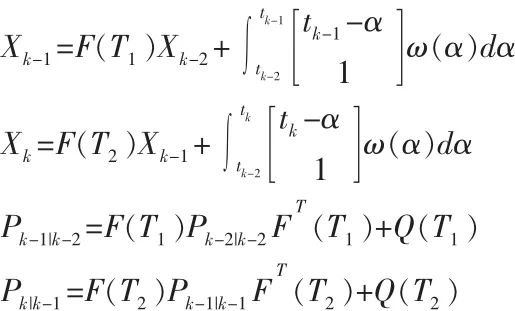
2.2 tk時刻用 Zk值更新

當測量值Zk到達濾波器用于處理時，濾波器并不知道延時測量值Zk-1的存在。因而，濾波器將繼續用標準卡爾曼濾波器更新處理。

首先處理將設計以前的狀態估計Xk-2

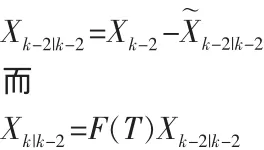
則狀態估計誤差為

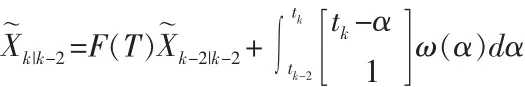
標準卡爾曼濾波處理應用增益更新狀態估計

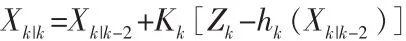
進而可求得

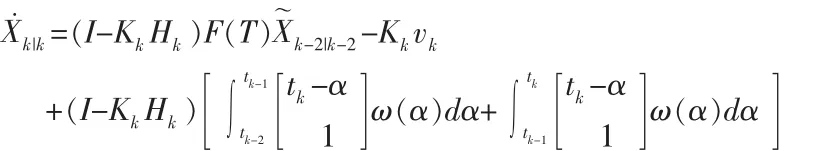
考慮到突發性，負時間更新可能在Xk-2|k-2→Xk|k更新時刻，定義量

該量為協方差，tk時刻標準更新后的狀態估計誤差X?k|k，時間間隔T前半部分的累積對象噪聲誤差。通過整理可得：

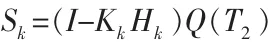
2.3 負時間更新算法

延時測量 Zk-1具有誤差 vk-1～N（0，Rk-1），在狀態估計更新 Xk|k被發現時，時刻狀態估計更新Xk|k+。下面確定的卡爾曼增益新Kk+

該項F－1（T2）Xk|k于計算tk-1時刻更新的新息，同時確保 tk-1時刻的估計值Xk|k+。 代入Zk和 Xk，則

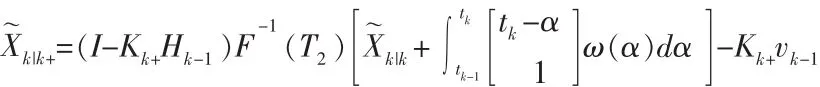
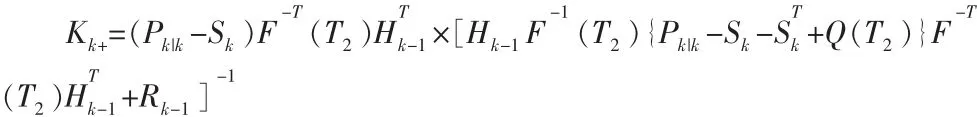
進而求得

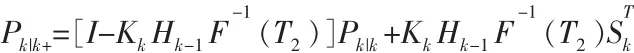
3 簡單算例

這里只用目標跟蹤的其中一個坐標，濾波器參數為：

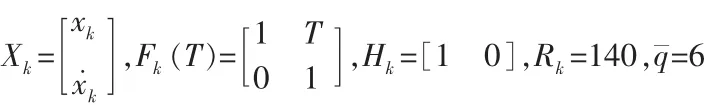
假定有4個測量值Zk，k=1，2，3，4，所有值的準時到達在1秒的間隔內。

為了對比分析最小均方差負時間更新方法和標準卡爾曼濾波公式的濾波結果，表1給出了三種不同情況下的最終協方差值：無延時測量值、缺失測量值Z3標準擴展卡爾曼濾波方法和Z3最后到達的負時間更新濾波方法。

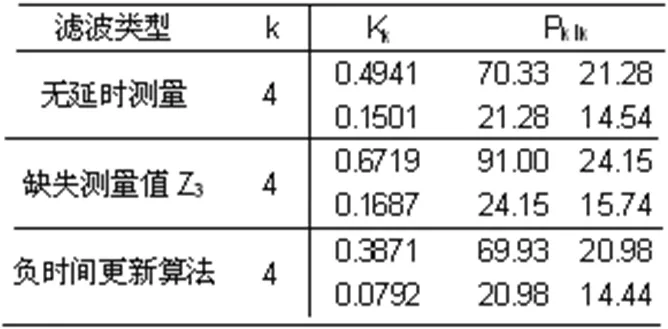
表1 三種不同情況下最終協方差值

由表1可知，丟棄延時量Z3情況下，時間間隔增加到2秒，協方差值變得很大，濾波增益也很大；采用負時間更新方法濾波得到的最終協方差值與無延遲測量值的擴展卡爾曼濾波值近似是一樣的。

4 結論

本文針對多平臺傳感器目標跟蹤的無序量測問題，給出了最小均方差負時間更新法的推導過程，并用簡單的例子驗證了采用負時間更新算法能夠取得較好的結果。

［1］韓崇昭，朱洪艷，段戰勝，等.多源信息融合[M].2版.北京：清華大學出版社，2010.

［2］黃細鳳，吳欽章.順序更新式無序量測處理算法[J].傳感技術學報，2012，2，25（2）.

［3］Bar Shalom Y.Update with Out-of-Sequence Measurements in Tracking：Exact Solution[J].IEEE Transactions on Aerospace Electronic Systems，2002，38(3)：769 －778.Hilton R D，Martin D A，Blair W D.

［4］Tracking with Time Delayed Data in Multi-Sensor Systems[R].Technical Report NSWCDD/TR－93/351，AD－A355269，Dahlgren，VA，August 1993.