Matlab 在建筑物沉降觀測數據處理中的應用研究

張志偉 張劍輝

(南京橋新建設有限公司，江蘇南京 211103)

1 概述

隨著科學技術的迅猛發展和我國現代化進程的不斷加快，城市各類高層、超高層建筑物和重要建筑物日益增多。隨著建筑物施工的進展，荷載不斷增加，在地基基礎和上部結構的共同作用下，建筑物將發生沉降。為了建筑物的施工使用安全，建筑物施工過程中，應加強沉降觀測及時掌握建筑工程沉降程度及沉降趨勢，處理沉降觀測結果，并采取合理的方法科學預測建筑物的沉降變形，為勘察、設計、施工等部門提供詳盡的一手資料，指導合理的施工工序，保證建筑物的正常使用壽命和建筑物的安全性。在沉降觀測數據處理中，建立沉降量預測模型、繪制沉降曲線是建筑物沉降觀測的重要內容。Matlab有一個功能強大的曲線擬合工具箱Curve Fitting Tool，使用方便。在Matlab完成繪制沉降曲線后，數據分析人員即能根據實際沉降曲線和Matlab工具箱提供的多種類型的線性、非線性曲線擬合形式，實現沉降量預測模型的建立。本文根據南京江寧區某小區其中一棟建筑物的沉降觀測數據為例，對Matlab在建筑物沉降觀測數據處理中的應用進行了研究。

2 M atlab Curve Fitting Tool工具箱簡介

Curve Fitting Tool工具箱提供用于曲線擬合數據的圖形工具和函數。使用該工具箱可進行數據分析、比較候選模型和刪除偏值等。本文涉及的主要功能有:用于曲線擬合的圖形工具。

使用自定義方程求解線性和非線性模型。

2.1 曲線擬合類型

Curve Fitting Tool工具箱提供的擬合類型有:Custom Equations:用戶自定義的函數類型;Exponential:指數函數，有2種類型:a*exp(b*x)，a*exp(b*x)+c*exp(d*x);Fourier:傅立葉函數，有7種類型，基礎型是a0+a1*cos(x*w)+b1*sin(x*w);Gaussian:高斯函數，有8種類型，基礎型是a1*exp(－((xb1)/c1)^2);Interpolant:插值函數，有 4種類型，linear，nearest neighbor，cubic spline，shape-preserving;Polynomial:多項式函數，有9 種類型，linear，quadratic，cubic，4-9th degree;Power:冪函數，有2 種類型:a*x^b，a*x^b+c;Rational:有理數函數，分子、分母共有的類型是 linear，quadratic，cubic，4-5th degree，此外，分子還包括 constant型;Smoothing Spline:平滑函數;Sum of Sin Functions:正弦曲線函數，有8種類型，基礎型是a1*sin(b1*x+c1);Weibull:只有1種，a*b*x^(b－1)*exp(－a*x^b)

2.2 應用

1)點擊Matlab左下角的Start→Toolboxes→Curve Fitting;2)點擊Curve Fitting Tool進入曲線擬合工具箱界面“Curve Fitting Tool”;3)在Data Sets頁面里的X Data選項中選取x向量，Y Data選項中選取y向量，此時Curve Fitting Tool窗口中顯示出這一數據組的散點分布圖;4)選擇好所需的擬合曲線類型及其子類型，并進行相關設置。——如果是非自定義的類型，根據實際需要點擊“Fit options”按鈕，設置擬合算法、修改待估計參數的上下限等參數;——如果選 Custom Equations，點擊“New”按鈕，彈出自定義函數等式窗口，有“Linear Equations線性等式”和“General Equations構造等式”兩種標簽。然后點擊OK。即可顯示出擬合結果(見圖1)，非常方便。

3 應用實例

南京江寧區某小區共有26棟高層住宅樓，其中第26棟建筑物的沉降點布置見圖2，其中3，7，11，14，17，21沉降觀測數據見表1。

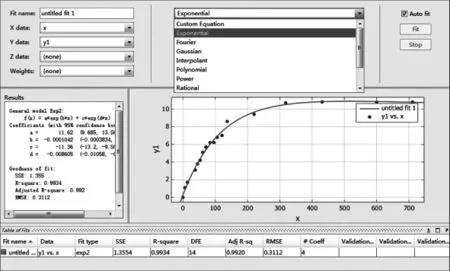
圖1 Curve Fitting Tool擬合結果圖

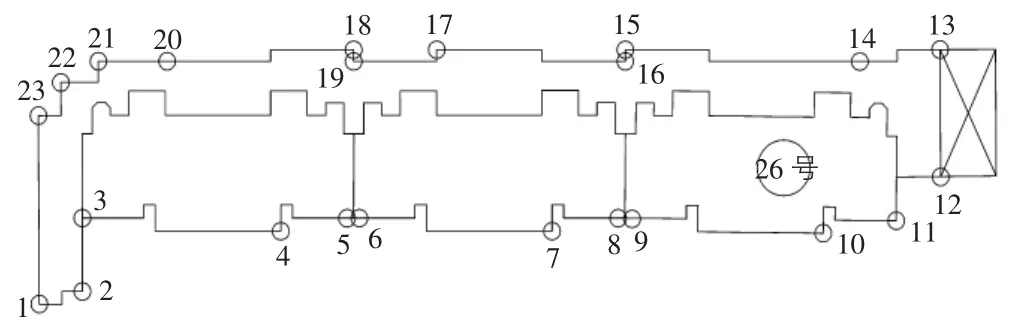
圖2 26棟沉降點布置圖

表1 沉降觀測數據表mm

為比較擬合模型的穩定性，選用 3，7，11，14，17，21 6 個點進行擬合。根據“Table of Fits”框中顯示的SSE(誤差平方和):擬合數據和原始數據對應點的誤差的平方和。SSE越接近0，說明模型選擇和擬合更好，數據預測也越成功;RMSE(均方根):回歸系統的擬合標準差;R-square(相關系數):其正常取值范圍為0～1，越接近1，表明方程的變量對y的解釋能力越強，這個模型對數據的擬合也越好。選用擬合函數為二項指數擬合，其擬合公式為y=a·ebx+c·edx。根據表1的數據，得擬合結果見表2。其中3號點的沉降量散點和擬和曲線圖見圖1。

表2 擬合結果表

從表2可以看出，這6個點的擬合函數系數相近，說明所選模型較穩定。

4 結語

本文利用Matlab Curve Fitting Tool工具箱對建筑物沉降觀測數據處理進行分析處理，建立預測模型。由于選擇模型是根據SSE，RMSE和R-square的數值比較而得，因此所建立的預測模型更具科學性，較符合實際情況。能更好的為指導施工、驗證設計計算參數、檢驗施工質量、建成后安全運營以及工程質量事故判斷與處理提供必要的數據支撐。

［1］陳 健.MATLAB在變形監測數據處理中的應用［J］.城市勘測，2009(2):130-133.

［2］基于MATLAB的高層建筑沉降變形監測數據處理［J］.測繪與空間地理信息，2010，32(5):3-5.

［3］石博強，滕貴法，李海鵬，等.Matlab數學計算范例教程［M］.北京:中國鐵道出版社，2004.

［4］張智星.MATLAB程序設計與應用［M］.北京:清華大學出版社，2002:4.

［5］王 劍，張書畢，史先領，等.MATLAB工具箱在測繪數據處理中的應用［J］.四川測繪，2006，29(1):17-20.

［6］毛濤濤，王正林，王 玲，等.精通MATLABGUI設計［M］.北京:電子工業出版社，2008.