最優樹算法的教學研究①
張愛平,李 強,陳志彬
(湖南工業大學理學院,湖南株洲412000)
在20世紀50年代,美國心理學家吉爾弗德在創造性思維方面作了深入的研究,認為創造性思維包括發散性思維、收斂性思維和直覺性思維等形式。教師若能在教學中巧妙地利用富有創新性的教學內容訓練學生的創造性思維,則能充分發揮教育的功能,調動學生的學習積極性,激發學生的創造性,發展學生的創造能力。發掘Kruskal“避圈法”求最優樹的方法,以此為實施創造性教育的典型題材,對學生開展多種創造性思維形式的訓練,這是研究性教學的一種嘗試。筆者試圖將創新的思想融入教學中,通過設置教學的問題情境,引導學生推廣“避圈法”求最優樹的方法,探索研究性教學的有效途徑,有效實施創造性教育。
一 實例引入及基本概念
例1在n個城市之間架設通訊線路,要求給出一個設計方案使得n個城市聯系起來,且總造價最少。
在現實生活中有許多這種類似的問題,如果用點表示城市,架設在城市之間的通訊線路用帶權的邊表示,則得到一個n階賦權圖,即關于n個城市的通訊網絡圖。這個最佳設計方案,用圖論的語言描述即歸結為在n階的賦權連通圖中求一棵最優樹的問題。
定義1 設G=[V,E]表示結點集為V,邊集為E的無向圖,稱圖 G中結點與邊的交替序列 Γ =vi0ej0vi1ej1…ejlvil為vi0到vil的通路,如果起點vi0與終點vil重合即vi0=vil,則稱Γ為回路。
定義2 連通無回路的無向圖稱為無向樹,用符號T表示。
定義3 設無向連通帶權圖G=[V,E,W],T是G的一棵生成樹,T的各邊權之和稱為T的權,記作W(T);圖G的所有生成樹中權最小的生成樹稱為圖G的最小生成樹;圖G在T中的邊稱為T的樹枝,不在T中的邊稱為T的弦。
定理[1]1 設G=[V,E]是n階m條邊的無向圖,則下面命題是等價的:
(1)G是樹。
(2)G中任意兩個結點之間存在唯一的路徑。
(3)G中無回路且m=n-1。
(4)G中無回路,但在任意兩個不同的結點之間加一條新邊后所得圖中有唯一的含有新邊的一個回路。
二 設置問題情境,培養學生的創造性思維
1956年Kruskal給出了用“避圈法”求最小生成樹的一個算法,算法第一步:首先將具有n個結點m條邊的帶權簡單連通圖G=[V,E,W]中的各條邊,按權從小到大依次序排列,如W(e1)≤W(e2)≤…≤W(em),其中e1的權最小,em的權最大;第二步:取權最小的兩條邊構成邊集T0={e1,e2},再從第三條邊e3開始,按次序逐個將各邊加進T0中去,如果出現回路,則將這條邊放棄不加進邊集T0中,按此法一直進行到T0中的邊數共計n-1條為止,則T0導出的邊子圖就是圖G的最小生成樹。
定理[1]2 “避圈法”對于帶權簡單連通圖 G=[ V,E,W ],按Kruskal“避圈法”導出的邊子圖T0是圖G的一棵最小生成樹,且其算法如下:
(1)在圖G的邊集E中選擇一條邊ei;
(2)若選好邊集 Ei= {e1,e2,…ei},則從邊集E-Ei中選取邊ei+1,其中邊ei+1滿足:
(ⅰ)邊導出圖G[ Ei∪ {ei+1}]無圈;
(ⅱ)W(ei+1)是符合(ⅰ)的條件下盡可能小的權;
(3)到第二步不能再進行時則停止。
求最小生成樹的Kruskal“避圈法”直觀明了,目前國內的《離散數學》教材向學生介紹的都是這種方法。該方法在不構成回路的條件下優先選擇圖G中權盡可能小的邊成為T0的邊,體現的是一種有序優化構造的思想,對學生的思維具有啟發性;對于這個知識點的教學可以通過設疑,向學生發問,引導學生思考求最優樹的方法;在引導學生對構成最優樹要素直觀認識的基礎上,鼓勵學生求同存異,積極開展發散性思維、收斂性思維和直覺性思維。
問題1 如果將Kruskal“避圈法”中圖G的邊由小到大排序改為由大到小排序,即優先有序選擇圖G中盡可能大的邊,同學們如何求帶權簡單連通圖G=[V,E,W]的最小生成樹?
問題2 類似Kruskal“避圈法”同學們能使用“破圈法”求帶權簡單連通圖G=[V,E,W ]的最小生成樹嗎?
問題3 用“避圈法”和“破圈法”求帶權簡單連通圖G=[V,E,W]的最小生成樹還有其它算法嗎?
以上的教學過程遵循呈現問題、解決問題和發現問題的途徑向學生展開,這樣做能較好地把發展學生的創造性思維與解決問題獲得知識緊密結合起來。下面是引導學生獲得的關于Kruskal“避圈法”推廣后的一些命題,其證明方法富有思想啟迪性,對學生的思維具有啟發性,是有序優化方法的具體應用。
命題1若將圖G的邊由大到小排序,則可用“破圈法”求帶權簡單連通圖G=[V,E,W]的最小生成樹,其算法過程表述為:
第一步:首先將具有n個結點m條邊的帶權簡單連通圖G=[V,E,W]中的各條邊,按權從大到小依次序排列,如W(e1)≥W(e2)≥…≥W(em),其中e1的權最大,em的權最小;
第二步:取權最大的邊e1,如果圖G=[V,E,W]中存在含有邊e1的圈,則刪去邊e1,得到邊集E1={e1},否則保留邊e1,得到子圖G1;
第三步:按邊的次序進行到第i步,如果在圖Gi-1中存在含有邊ei的圈,則刪去邊ei,得到邊集Ei=Ei-1∪{ei},否則保留邊ei,得到子圖Gi,按此法一直進行到Ei中的邊數共計m-n+1條為止,則子圖Gi就是圖G的最小生成樹。
證明設n個結點m條邊的帶權簡單連通圖G的最小生成樹為T,用“破圈法”得到的生成樹為T0,若能證明T0的權與T的權相同,則T0是圖G的一棵最小生成樹。
首先將T0的邊按權由大到小排列,不妨設為T0={e1,e2,…en-1},下面分兩種情形證明T0是圖G的一棵最小生成樹:
(ⅰ)當T0與T無公共邊時:將T0中的最大邊e1加到T上,由定理1可知必存在一條包含e1的唯一的回路C;在回路C中必存在一條異與e1不是T0的邊a且W(a)≥W(e1),否則,在構造T0時e1?T0;將邊a刪除,得到一棵新的生成樹T1=T∪{e1}-{a}且樹的權為
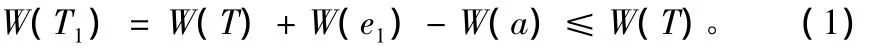
由于T是最小生成樹,即有W(T1)≥W(T),結合(1)式得W(e1)=W(a),這樣T1是一棵最小生成樹,且與T0有一條公共邊e1;用T1取代T,再將e2加到T上,同理可得一棵新的生成樹T2且T2∩T0={e1,e2},即T2與T0有兩條公共邊。
根據以上分析作一歸納假設:設T0與T有i條權是相繼遞減的公共邊,不妨設為e1,e2,…ei(1≤i≤n-1),對于不在T中而在T0中的第i+1條邊ei+1加到T上,由定理1可知必存在一條包含ei+1的唯一的回路C;在回路C中至少存在一條異與 e1,e2,…ei不是 T0中的邊 b且 W(b)≥W(ei+1),否則,在構造 T0時 e1,e2,…ei,ei+1中至少有一條邊不在T0中;將b刪除,得到一棵新的生成樹Ti+1=T∪{ ei+1}-{b}且樹的權為
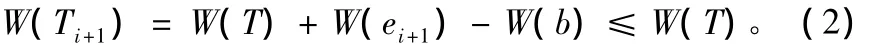
由于T是最小生成樹,即有W(Ti+1)≥W(T),結合(2)式得W(ei+1)=W(b),這樣Ti+1是一棵最小生成樹,且與 T0有 i+1 條公共邊 e1,e2,…ei,ei+1;用 Ti+1取代 T,重復以上過程直到T與T0有n-1條公共邊為止,得到T0與T有權完全相同的邊序列,于是T0也是圖G的一棵最小生成樹。
(ⅱ)當T0與T有不是權相繼遞減的公共邊時:令,不妨設f(T)=k≥1,這表明ei∈T0∩T(i=1,2,…k-1)即邊的權相繼遞減,但邊ek∈T0而ek?T;類似情形(ⅰ)的證明,將邊ek加到T上,由定理1可知必存在一條包含ek的唯一的回路C,在回路C中至少存在一條異與e1,e2,…ek-1不是T0中的邊g且W(g)≥W(ek),于是得到一棵新的生成樹Tk=T∪{ek}-{ g}且樹的權為
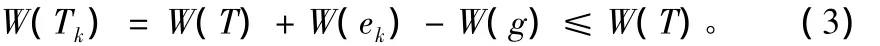
由于T是最小生成樹,即有W(Tk)≥W(T),結合(3)式得W(ek)=W(g),這樣Tk是一棵最小生成樹,且與T0有k條權公共邊e1,e2,…ek;用Tk取代T,重復以上過程,可以保證公共邊的權為相繼遞減直到T與T0有n-1條公共邊為止,得到T0與T有權完全相同的邊序列,于是T0也是圖G的一棵最小生成樹。
在教學中以命題的形式啟發學生解決問題,然后在解決問題中讓學生發現問題,這是開展研究性數學教學不可缺少的一個重要環節。在定理2和命題1的基礎上,圍繞“避圈法”“破圈法”進一步激發學生的發散思維和直覺思維,引導學生思考求最優樹的方法,不難會獲得下面的兩個命題:
命題[2]2 若不對圖G的邊排序,則同樣可用“破圈法”求帶權簡單連通圖G=[V,E,W ]的最小生成樹,其算法表述為:
第一步:任取G中的一個回路,刪除這個回路中權最大的邊得到子圖G1;
第二步:再在G1中任取一個回路,刪除這個回路中權最大的邊得到子圖G2;
第三步:如此下去進行到第i步得到子圖Gi,在Gi中任取一個回路,刪除這個回路中權最大的邊得到子圖Gi+1,直到子圖Gi+1無回路為止,則子圖Gi+1是圖G的最小生成樹。
命題3若任意選取圖G中的結點而不是回路,則可用“避圈法”求帶權簡單連通圖G=[V,E,W]的最小生成樹,其算法表述為:
第一步:置邊集T為空集:
第二步:任選取圖G中的一個結點vi1,得結點集合V1={}與=V-V1,在圖G中,選取結點集合V1到中相關聯的權盡可能小的邊(vi1,vvi2,),并將此邊放入T中,結點放入V1中,此時結點集合
第三步:在圖G中選取結點v∈V1,u∈的權盡可能小的邊(v,u)且與原T中的邊不構成回路,同樣將此邊放入T中,結點u放入V1中;如此繼續直到V1=V,得到邊集T的邊導出圖則是圖G的最小生成樹。
命題2與命題3的證明類似命題1,故略去。
三 結語
總之,若能運用知識的多樣性,選擇與現實生活聯系密切、富有思想性的內容實施研究性教學,則能較好地激發學生探索問題的興趣,讓學生逐步形成辯證思考問題的思維習慣,啟迪他們的創造性思維,提高他們的創新能力;在解決問題中,讓他們能較好地發現條件與結論、知識與方法之間的內在聯系,獲得解決問題的正確方法。以上關于Kruskal“避圈法”開展研究性教學內容的嘗試,旨在拋磚引玉。
[1]屈婉玲,耿素云,張立昂.離散數學[M].北京:高等教育出版社,2007.
[2]陳正一.破圈法求最優樹的一個簡單證明[J].哈爾濱船舶工程學院學報,1990,11(4):236 -237.
[3]張德琇.創造性思維的發展與教學[M].長沙:湖南師范大學出版社,1990.

