基于離散元法的桿系結構幾何非線性大變形分析

齊 念 葉繼紅

(東南大學混凝土及預應力混凝土結構教育部重點實驗室，南京 210096)

在工程實際分析時，經常會遇到由幾何非線性所引起的結構大變形問題，這類問題的特點是伴隨大位移和大轉動，因此必須考慮變形對平衡的影響.對于桿系結構幾何非線性大變形問題，有限元法是目前最為常用的分析方法，學者們也提出了多種計算格式，如完全拉格朗日(TL)法、更新拉格朗日(UL)法和協同轉動法等［1-3］.但是，這些傳統方法在處理幾何非線性行為時，需要不斷集成和修正切線剛度矩陣，經常會遇到剛度矩陣奇異或非線性方程迭代求解不易收斂等問題，需要對方法本身進行特殊處理，導致計算效率偏低.

離散元法(discrete element method，DEM)最早由美國學者Cundall等［4］提出，現已發展成為計算散體力學領域中一種新的數值方法.該方法直接應用牛頓第二定律，單元之間采用彈簧系統連接，接觸力與接觸位移之間的關系構成了DEM的接觸本構模型.由于不要求滿足位移連續和變形協調條件，因此它特別適用于各種非連續、非均勻以及結構大變形和失效破壞等復雜過程及其機理的研究［5］.最初DEM 法的研究對象主要是散土體材料，如今已在許多工程領域如巖體邊坡滑動［6］、鋼筋混凝土梁的斷裂模擬［7］等方面取得了較好的應用.

DEM法在桿系結構中的應用還較少.本文提出將DEM法用于求解桿系結構(二維、三維)的幾何非線性大變形問題.對3個經典算例的靜力大變形問題及非線性動力行為進行了模擬，結果表明DEM法適宜于處理結構大變形問題.

1 DEM法

DEM法的基本思想是把研究對象離散成剛性單元的集合.任取一個單元α，設有n個單元與其相鄰，作用在單元 α上的外力為 Fext，外力矩為Mext.根據牛頓第二定律，其運動控制方程為

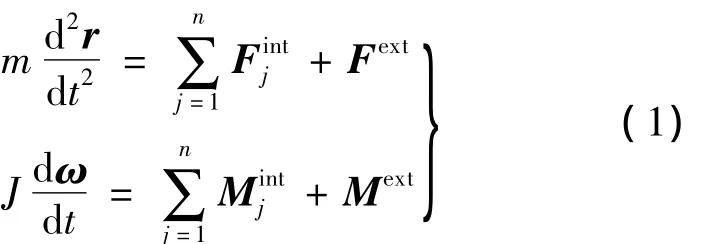
式中，m，J分別為單元α的質量和轉動慣量;r，ω分別為單元α的位置矢量和角速度矢量;分別為相鄰單元j對單元α產生的接觸力和接觸力矩;t為時間.

1.1 單元間的接觸本構模型

圖1 相鄰單元之間的接觸模型

在接觸平面內將接觸力和接觸力矩按矢量法則進行分解，得

將F和M分別向3個坐標軸進行投影，得

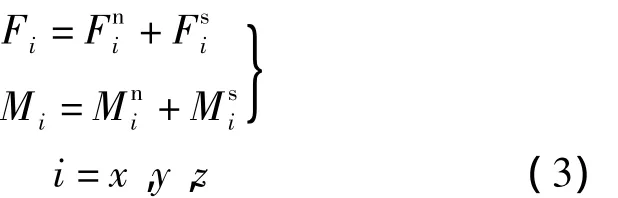
利用離散元法計算接觸力和接觸力矩時采用增量形式.在時間步長Δt內，由位移增量所引起的接觸力增量為

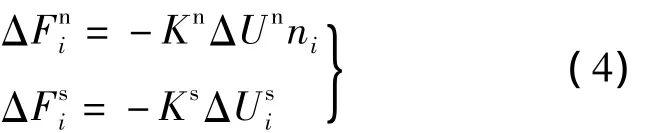
式中，Kn，Ks分別為彈簧法向剛度和切向剛度系數;ni(i=x，y，z)為 n 在3個坐標軸上的分量;分別為法向和切向相對位移增量，可通過接觸點C處的速度計算得到.

接觸力矩的計算過程與接觸力的計算過程相似.在時間步長Δt內，球A與球B之間的相對轉角增量所引起的接觸力矩增量為

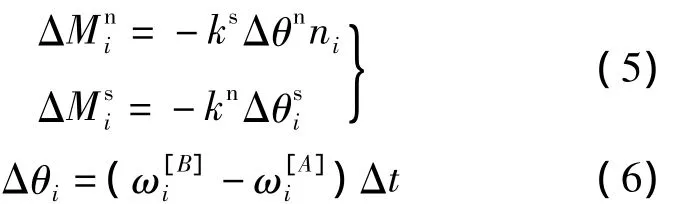
式中，kn，ks分別為彈簧轉動法向剛度和切向剛度系數;分別為法向和切向相對轉角增量.

1.2 時間步長的確定

在求解運動方程時，DEM通常采用顯示中心差分算法.中心差分法是條件穩定算法，其計算時間步長Δt必須小于由該問題所決定的某個臨界值Δtcr，否則算法將不穩定.

臨界值Δtcr的確定應同時滿足結構物理步長和數學計算步長的要求.物理步長是指結構中彈性波來回一次所需要的時間，框架結構的物理步長約為1 ms［9］.數學計算步長是指積分計算所需的時間步長，對中心差分法而言，解的穩定性條件為

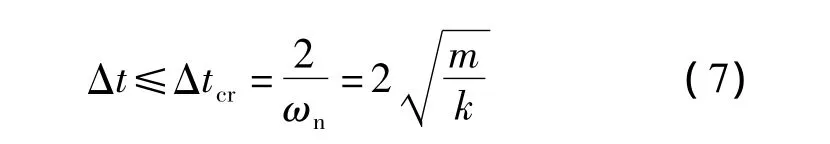
式中，ωn為結構的最高階固有振動頻率;m為結構質量;k為結構剛度.

本文在確定數學計算步長時，按如下方法粗略估計臨界值Δtcr:將式(7)中的k值取為1.1節中提到的4個彈簧剛度系數中的最大值，即

最后，通過比較物理步長與數學計算步長的臨界值，取二者較小值，以確定時間步長Δt的大小.

2 動力與靜力解及大變形問題

與傳統的結構靜力分析不同，離散元法本質上是求解結構的動力問題，因為式(1)的解本身就是結構的動力反應.

對于需要計算靜力解的問題，可采用阻尼耗能或緩慢施加外荷載的方式來逼近結構的靜止狀態.本文是在運動方程式中添加一項阻尼力，利用阻尼產生的逆向運動來達到削減結構動力響應的目的.這里采用局部非線性黏滯阻尼形式［8］，其本質是在單元的合外力基礎上，總體施加一個與其方向相反的作用力.單元α的阻尼力可表示為

式中，為阻尼系數，取值范圍為0～1;F*為單元α的廣義力;V*為單元α的廣義速度.需要說明的是，此處的阻尼并非結構的真實阻尼，它實際上是一個虛擬的行為，其目的是為了獲得結構的靜力解而選擇的一種耗能機制.

分析傳統結構時，小變形和大變形問題是需要進行嚴格區分的.前者的幾何方程為線性的，而后者的幾何方程則為非線性的.利用有限元法處理大變形問題時，一般是對單元切線剛度矩陣進行修正，采用增量迭代的方法求解結構的響應.而利用DEM法求解此類問題時，并不需要刻意區分是小變形還是大變形，因為在建立運動控制方程時并不涉及到幾何方程，也不要求位移連續，無需組集剛度矩陣和迭代求解，這與有限元法有著本質的區別.因此，將DEM法用于結構分析時，可以采用統一的步驟分析結構的小變形和大變形問題，其計算流程圖見圖2.

3 彈簧接觸剛度系數的確定

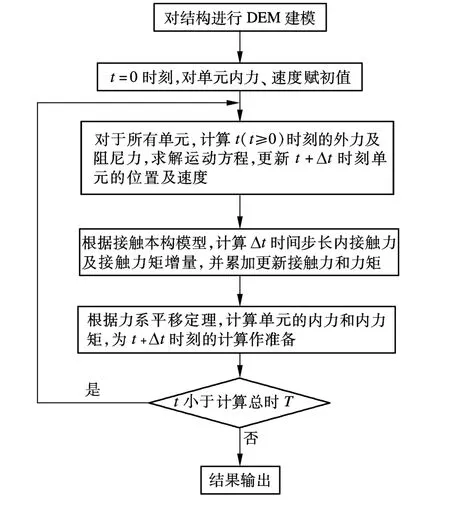
圖2 DEM法的計算流程圖

根據DEM法的基本理論，利用式(4)和(5)計算接觸力和接觸力矩增量時，需要事先給定彈簧接觸剛度系數的值.本文的研究對象主要是連續體——框架結構，而傳統的DEM法彈簧接觸剛度系數計算公式是基于散粒體的，不適用于框架結構［10］.基于簡單梁理論，將通過彈簧連接的2個圓球比擬成1根梁(見圖3).圖3中，RA，RB分別為球A和球B的半徑;L=RA+RB為梁的長度.設結構構件的截面積為S，截面慣性矩為I，扭轉慣性矩為J，彈性模量和剪切模量分別為E和G.

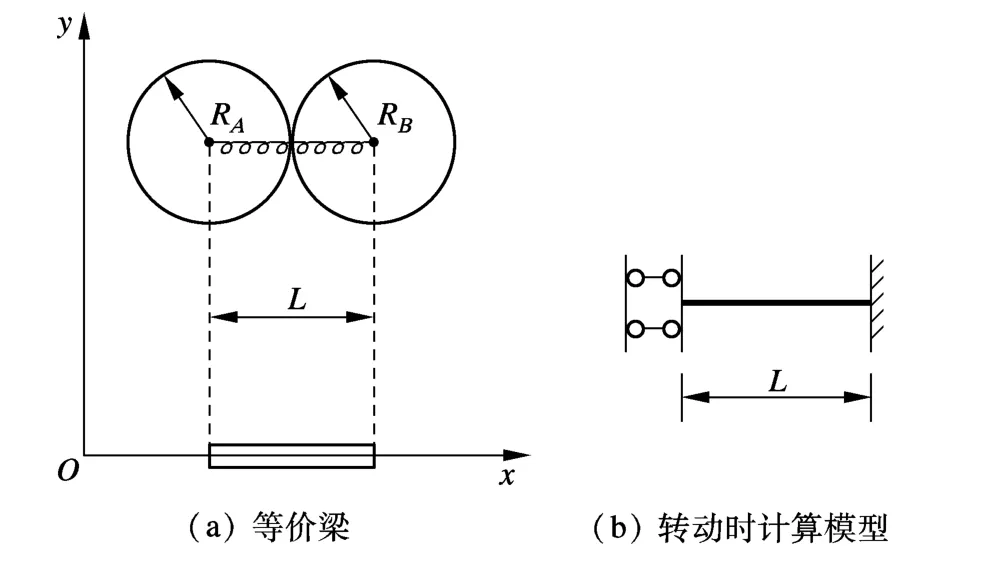
圖3 彈簧接觸剛度的等價梁模型

根據結構力學中桿端力與桿端位移之間的關系，可以得到彈簧接觸剛度計算公式.梁的軸向剛度系數Kn和切向剛度系數Ks分別為

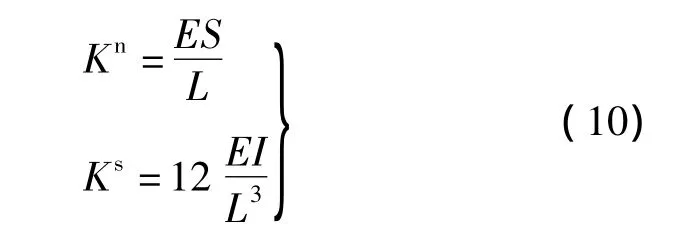
2個單元之間發生相對轉動產生轉角Δθ，Δθ可分解成平行于接觸面內的切向分量Δθs和垂直于接觸面內的法向分量Δθn.切向分量Δθs所引起的接觸力矩，與一端固定一端滑動的梁所產生的桿端彎矩等效.因此，轉動法向剛度系數為

垂直于接觸面內的轉角法向分量Δθn引起的則是扭矩.若是平面問題，扭矩為0;對于一般空間問題，扭矩可根據截面扭轉剛度與扭轉角相乘得到.因此，轉動切向剛度系數為

利用1個空間懸臂梁對該方法進行驗證.梁長L=200 mm，其截面呈圓環形，外徑φ=8 mm，壁厚 δ=0.5 mm，彈性模量 E=200 kN/mm2，剪切模量G=80 kN/mm2.梁端部承受集中力F=10 N，彎矩M=100 N·mm，扭矩T=2 kN·mm，材料為線彈性.懸臂梁DEM計算模型如圖4所示.在模擬時將最左端圓球固定，因為是求解靜力問題，取阻尼系數 =0.7，時間步長 Δt=1 ms.

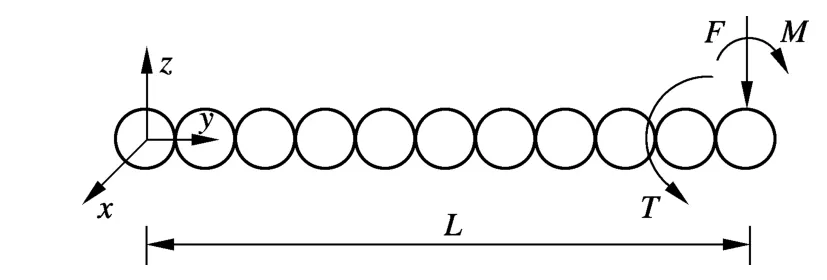
圖4 懸臂梁DEM計算模型

懸臂梁的變形和內力計算結果見表1.由表可知，根據DEM法計算的懸臂梁變形及結構內力與理論解相比，最大誤差僅為0.3%，說明本文確定彈簧接觸剛度系數及Δt的方法是正確合理的.

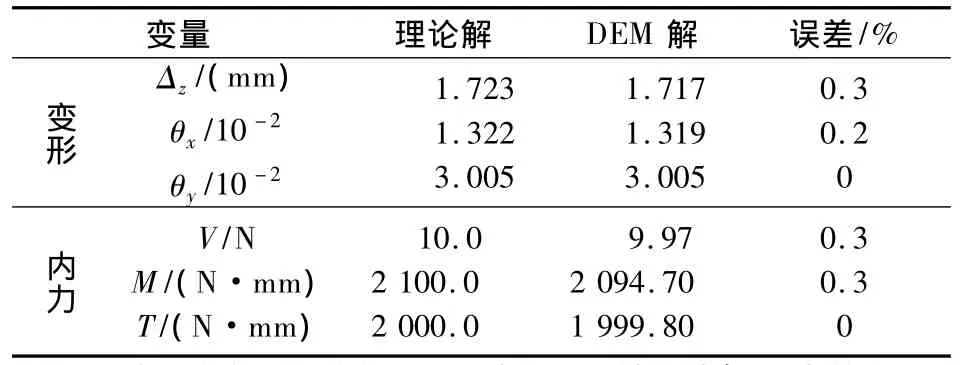
表1 集中力和力矩作用下的懸臂梁計算結果

4 數值算例

根據DEM法的基本原理及計算流程，編制了空間框架結構幾何非線性大變形分析程序.通過對文獻中常被引用的3個典型算例進行模擬和分析，驗證本文方法的正確性和適用性.

4.1 平面正方形剛架的大變形分析

如圖5(a)所示，平面正方形剛架各構件的材料和尺寸均相同，相關幾何及物理參數為:l=10 cm，S=0.5 cm2，I=0.0104 cm4，E=16 MN/cm2，材料為線彈性，P為外力.DEM計算模型如圖5(b)所示，球半徑取為1 cm，時間步長Δt=0.5 ms，阻尼系數 =0.7，材料密度取為單位1.

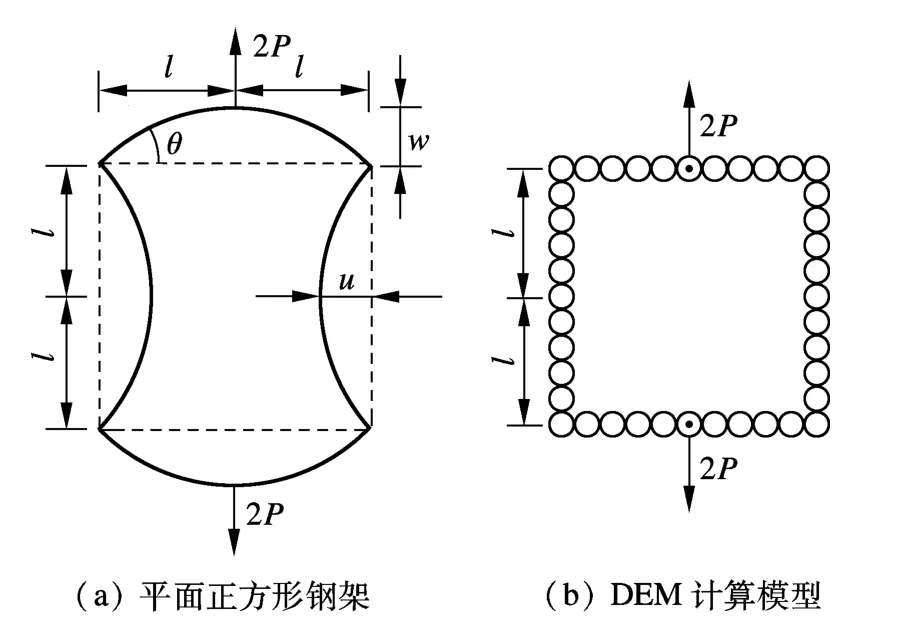
圖5 平面正方形剛架及離散元模型

圖6為利用DEM法計算得到的荷載-變形曲線.與文獻［11］中采用橢圓積分計算的結果進行對比，發現位移及轉角的計算值均與文獻解相吻合，最大誤差不超過1%.

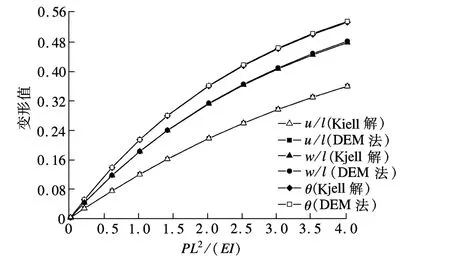
圖6 平面正方形剛架對邊受拉下的荷載-變形曲線

4.2 懸臂梁的大彎曲問題

如圖7所示，在懸臂梁端部作用一集中彎矩M(t).彎矩隨時間逐漸增加，梁將會由原來的靜止狀態彎成圓形或螺旋形.該典型算例常被用于結構大變形問題的分析中［12-13］.梁的相關幾何參數及物理參數采用文獻［12］中的數據，彎矩作用方式采用如圖8所示的線性漸增荷載，DEM模擬時將梁離散成9個半徑為1.25 mm的圓球.

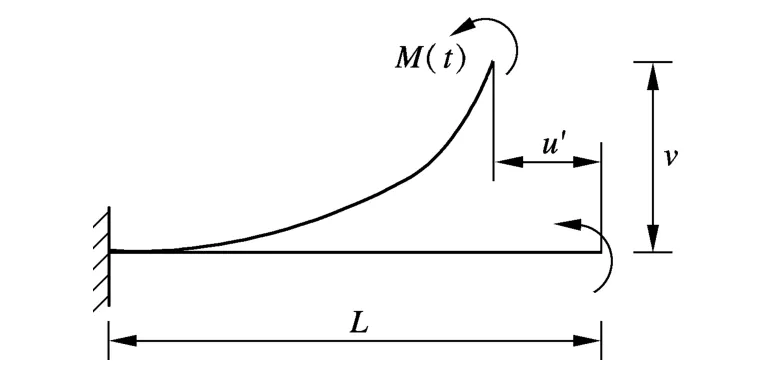
圖7 受端彎矩作用的懸臂梁

下面分2種工況對該梁的大彎曲行為進行數值模擬.

圖8 端部彎矩作用方式

工況1 對梁進行緩慢加載，如圖8(a)所示.取Δt=1 ms，=0.7.在該彎矩作用下梁最終將彎成一個圓.由于加載速率很慢，同時又有阻尼的耗能作用，因此實際上是模擬結構的近似靜力變形行為.表2為利用DEM法得到的梁自由端計算結果，與解析解［13］相比，兩者最大誤差為 0.6%，說明本文方法具有較高的精度.

表2 彎矩作用下懸臂梁自由端計算結果

工況2 梁的幾何及材料參數與工況1相同，但梁端彎矩加載方式如圖8(b)所示，阻尼系數 =0.1.利用DEM 法對其進行模擬，圖9是懸臂梁分別于時間 t=9，10，11，13 s時的形狀，發現梁最后卷曲成螺旋狀，而非工況1中的圓形.這是因為此時的計算結果為動態解，與所采用的阻尼系數和加載速率有關，若保持最終加載力不變，隨著時間的延續，由于阻尼耗能，動態解最終也會趨于靜力解，螺旋狀也將趨于圓狀.

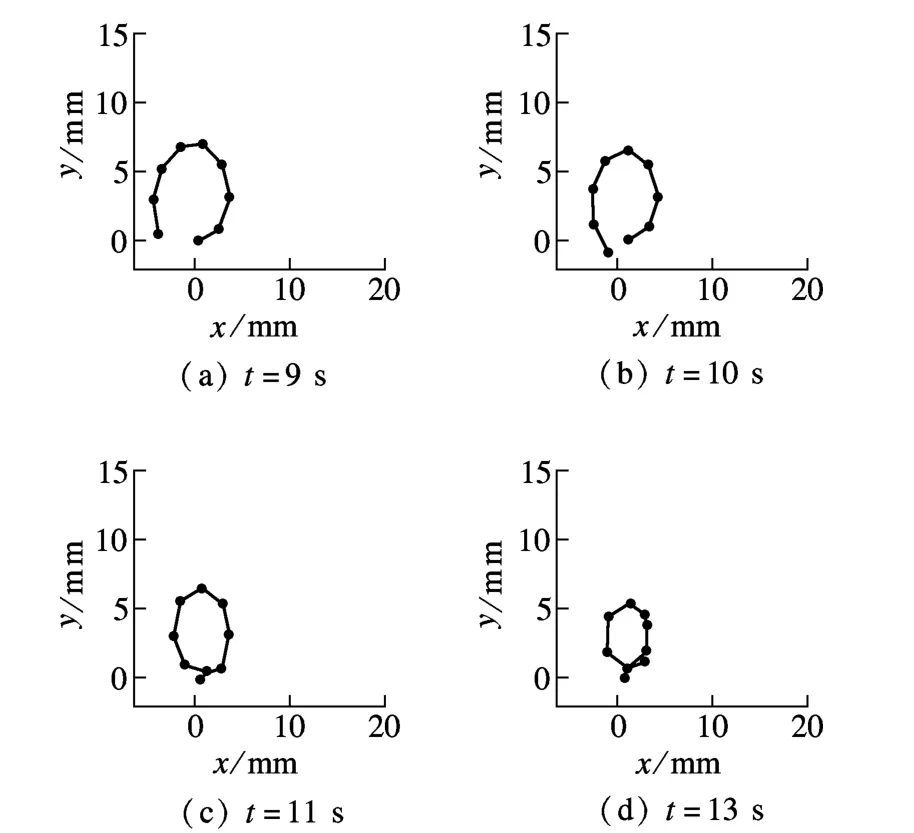
圖9 不同時刻懸臂梁的形狀

4.3 六角形空間剛架的大變形分析

對于如圖10所示的六角形空間剛架，結構的6個支座均為鉸約束，各構件截面均為正方形，其幾何物理參數的取值與文獻［14］保持一致.利用DEM法進行模擬時，將構件離散成24個球單元，取 Δt=0.1 ms， =0.7，材料密度取為單位 1.

圖10 六角形空間剛架(單位:mm)

對該結構進行幾何非線性靜力大變形分析.表3為利用DEM法得到的剛架頂點荷載-位移計算結果.由表可知，與文獻［14］中利用有限元法分析的結果進行對比，兩者最大誤差不超過0.9%.

表3 六角形空間剛架頂點的荷載-位移結果

5 結論

1)本文將DEM法推廣應用于桿系結構(二維、三維)的幾何非線性大變形問題.基于簡單梁理論，推導了適用于桿系結構分析的彈簧接觸剛度系數計算公式，并利用算例對其正確性進行了檢驗.

2)基于本文推導的剛度系數計算公式，對桿系結構的幾何非線性大變形問題進行分析.列出了3個典型數值算例，即2個平面框架和1個空間網格結構，分別對其靜力和動力大變形行為進行了模擬，并將結果與其他計算方法的結果進行比較，兩者吻合良好.此外，離散元法在處理幾何非線性時無需組集剛度矩陣，也不用迭代求解非線性方程，故該方法適宜于處理桿系結構的大變形問題.

3)DEM法本質上是求解結構的動力行為，對于需要計算靜力解的問題則是通過增加阻尼項來進行模擬的.阻尼系數 的選取應根據分析問題的性質合理確定，對于靜力解問題，綜合考慮數值精度和計算效率，建議可取 =0.7.由于DEM 法是采用中心差分法求解運動方程，計算時間步長Δt的值一般取0.1～1 ms.所提的時間步長臨界值估算方法，可供結構分析時借鑒.

References)

［1］Teh L H，Clarke M J.Co-rotational and lagrangian formulations for elastic three-dimensional beam finite element［J］.Journal of Constructional Steel Research，1998，48(3):123-144.

［2］Yang Y B，Lin S P，Leu L J.Solution strategy and rigid element for nonlinear analysis of elastically structures based on updated Lagrangian formulation［J］.Engineering Structures，2007，29(6):1189-1200.

［3］Thanh N L，Jean M B，Mohammed H.Efficient formulation for dynamics of co-rotational 2D beams［J］.Computational Mechanics，2011，48(2):153-161.

［4］Cundall P A，Strack O D L.A discrete numerical model for granular assemblies［J］.Geotechnique，1979，29(1):47-65.

［5］劉凱欣，高凌天.離散元法研究的評述［J］.力學進展，2003，33(4):483-490.Liu Kaixin，Gao Lingtian.A review of the discrete element method ［J］.Advances in Mechanics，2003，33(4):483-490.(in Chinese)

［6］James F H，David S C，William S P.Simulation of unstable fault slip in Granite using a bonded-particle model［J］.Pure and Applied Geophysics，2002，159(1/2/3):221-245.

［7］Azevedo N M，Lemos J V，Almeida J R.A discrete particle model for reinforced concrete fracture analysis［J］.Structural Engineering and Mechanics，2010，36(3):1-19.

［8］Cundall P A.PFC user's manual(version 3.1)［M］.Minneapolis，MN，USA:Itasca Consulting Group，Inc.，2004.

［9］喻瑩.基于有限質點法的空間鋼結構連續倒塌破壞研究［D］.杭州:浙江大學建筑工程學院，2010.

［10］徐小敏，凌道盛，陳云敏，等.基于線性接觸模型的顆粒材料細宏觀彈性常數相關關系研究［J］.巖土工程學報，2010，32(7):991-998.Xu Xiaomin，Ling Daosheng，Chen Yunmin，et al.Correlation of microscopic and macroscopic elastic constants of granular materials based on linear contact model［J］.Chinese Journal of Geotechnical Engineering，2010，32(7):991-998.(in Chinese)

［11］Kjell M.Numerical results from large deflection beam and frame problems analysed by means of elliptic integrals［J］.International Journal for Numerical Methods in Engineering，1981，17(1):145-153.

［12］Wu Tongyue，Wang Renzuo，Wang Chungyue.Large deflection analysis of flexible planar frames［J］.Journal of the Chinese Institute of Engineers，2006，29(4):593-606.

［13］丁承先，段元鋒，吳東岳.向量式結構力學［M］.北京:科學出版社，2012:273-278.

［14］Shugyo M.Elastoplastic large deflection analysis of three-dimensional steel frames［J］.Journal of Structural Engineering，ASCE，2003，129(9):1259-1267.