貝葉斯網絡在半導體設備故障診斷中的應用

郝曉亮

(中國電子科技集團公司第十三研究所，河北石家莊 050051)

科技的進步帶動了半導體行業的快速發展，半導體工藝越來越復雜，對設備可靠性的要求也越來越高，設備也在朝著大型化、自動化、智能化、集成化方向發展。設備中的各個部件之間關系復雜，設備一旦出現故障，會對整個生產線造成重大影響。如何能夠快速地確定并解決設備的故障，越來越受到人們的關注。人工智能和計算機技術的快速發展給故障診斷指出了一個發展方向，即智能故障診斷。目前有很多智能診斷的方法：故障樹分析法、神經網絡系統、智能專家系統、馬爾科夫可靠性模型、概率因果網絡、貝葉斯網絡等。

由于設備的復雜性，知識的不完備性，以及檢測手段的局限性，使得設備的故障診斷具有很大的不確定性。在故障診斷領域，不確定性是一個普遍現象。貝葉斯網絡以其在處理不確定性問題的強大能力，豐富的概率表達能力越來越受到人們的重視[1]。

1 貝葉斯網絡概述

貝葉斯網絡（Bayesian Network）又稱貝葉斯信念網絡，是描述隨機變量（事件）之間依賴關系的一種圖形模式，是目前不確定性知識表達和推理領域最有效的理論模型之一[2]，適用于不確定性和概率推理的知識表達和推理[2]。

貝葉斯網絡由兩部分構成，一是貝葉斯網絡結構圖，另一部分是條件概率表（Conditional Probability Table，CPT）。

1.1 貝葉斯網絡結構圖

貝葉斯網絡結構圖是一個有向無環圖（Directed Acylic Graph，DAG）[2]，是貝葉斯網絡的定性表示。圖中的節點表示事件中的變量，節點之間用有向弧線連接，弧線指向的是子節點，弧線的另一端是父節點，表示的是兩個事件的因果關系。沒有任何弧線指向的節點是根節點。

1.2 條件概率表

條件概率表是貝葉斯網絡的定性表達，表示的是網絡中各個節點之間的影響程度，是用概率分布來表示的，由一系列的概率值組成。

1.3 貝葉斯定理

貝葉斯網絡的理論基礎是貝葉斯定理，貝葉斯網絡是在貝葉斯定理基礎上發展起來的用于系統的描述和解決概率問題的圖形，可以從事件發生的結果去反推引起事件發生的各個原因的概率大小。在故障診斷時，最常見的問題是已知故障發生，要尋找故障發生的原因，即“執果尋因”。因此，貝葉斯定理在故障診斷領域應用廣泛。

貝葉斯定理:設實驗E的樣本空間S。A為E的事件，B1B2，...Bn為S的一個劃分，且P(A)>0，P(Bi)>0(i=1，2，...n)，則

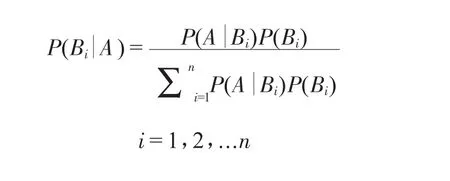
1.4 貝葉斯網絡故障診斷中常用的概念

這里介紹貝葉斯網絡故障診斷技術中常用的幾個概念：先驗概率，后驗概率，條件概率，條件獨立性假設。

先驗概率

先驗概率是人們事先對事件發生的概率大小的估計，該類概率是人們估計的概率，沒有經過驗證，是檢驗前的概率，稱之為先驗概率，通常是由領域內的專家或根據設備的歷史資料來確定。

后驗概率

后驗概率是人們在經過調查等方式取得了新的證據，再利用貝葉斯公式，計算出的更接近于實際情況的概率。

條件概率

設A、B是兩個事件且P(A)>0，則稱概率

為事件B在事件A發生下的條件概率。條件獨立性假設

設有隨機事件A、B、C，如果A、B關于C條件獨立，則有

這說明，在事件C發生的條件下，事件A的發生與否，與B無關。條件獨立性假設能簡化網絡推理的過程，還能大大減少網絡推理所需要的先驗概率的數量。

2 貝葉斯網絡的故障診斷原理

假設事件A、B是導致事件C發生的兩個原因，假設事件A發生的概率是0.2；事件B發生的概率是0.4；事件A發生，B也發生時，事件C發生的概率是0.95；事件A發生，事件B不發生時，事件C發生的概率是0.8；事件A不發生，事件B發生時，事件C發生的概率是0.9；事件A、事件B都不發生時，事件C發生的概率是0.1；即：

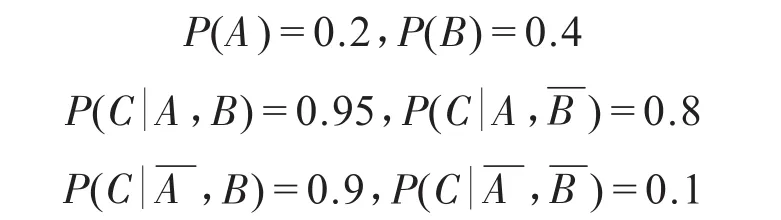
此事件的貝葉斯網絡結構圖如圖1、圖2所示。

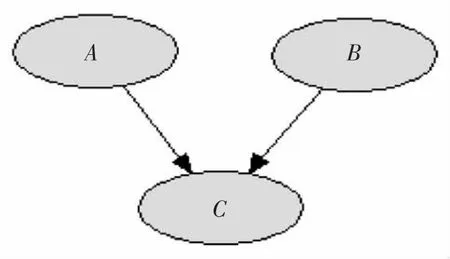
圖1 貝葉斯網絡結構圖

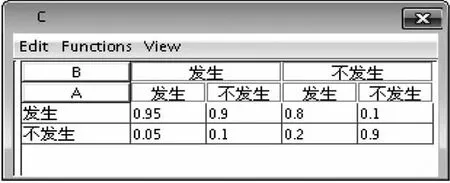
圖2 事件C的條件概率表

在已知的條件下，計算如果事件C發生，事件A、事件B發生的概率。先計算事件A發生的概率。

根據貝葉斯定理

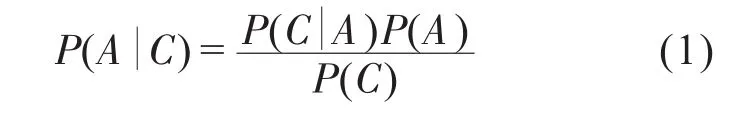
其中，P(C)是在不考慮事件A、B的是否發生，事件C發生的概率，可以用全概率公式計算：

將上面計算的數據代入到公式(1)中，得：

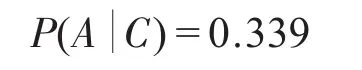
同理可以得出：

通過以上的分析可以得知，在已知事件C發生的情況下，事件B發生的概率要比事件A要大。這種分析方法可以應用于故障診斷領域，在故障診斷領域，常見問題是已知了設備的故障，想找到引起故障的原因，利用貝葉斯網絡故障診斷技術，可以方便的知道引起設備故障的各個原因的概率。根據這個概率的大小來指導下一步的維修。貝葉斯網絡故障診斷的原理就是“執果尋因”，通過已知的證據以及先驗概率，利用貝葉斯定理來計算在已經故障（證據）的前提下，引起故障的各個原因的條件概率的大小。

3 貝葉斯網絡故障診斷的過程

目前在貝葉斯網絡故障診斷領域常用的模型是故障—征兆（Failure-Symptom）模型。在此模型中，根據網絡中各個節點的性質分為故障原因節點和故障征兆節點。故障原因節點是導致故障發生的最根本的原因，通常不容易觀察和檢測。故障征兆節點通常可以通過觀察、測量或檢修等操作確定該節點的狀態，此節點的狀態可以作為證據輸入到網絡中。

貝葉斯網絡故障診斷過程通常有以下幾個步驟：

（1）將整個事件中的子事件列出，這些就是網絡中的節點，根據節點的性質分為故障原因節點和故障征兆節點。

（2）確定貝葉斯網絡中各個節點之間的關系，網絡中節點之間的因果關系通常由領域內的經驗豐富的專家，或者根據設備的歷史資料確定。

（3）給定各個節點的條件概率表。這些概率都是先驗概率，包括故障原因節點的概率以及故障征兆節點在故障原因節點狀態已知下的條件概率。確定方法前文已經說過。

（4）通過觀察、檢測、檢修故障征兆節點確定一個證據。

（5）將證據輸入到貝葉斯網絡中，利用貝葉斯定理，結合網絡結構和條件概率表，計算各個節點在已知證據下的條件概率值，根據計算出的結果，找出概率最大的節點。

（6）檢測并修復概率最大的節點，如果故障排除，診斷結束。如果故障未排除，此節點的狀態信息就是另一個證據。返回第5步。直到找出故障的真正原因。

通過貝葉斯網絡的故障診斷可以計算出出現故障后，引起故障的各個原因的概率值，通過這些概率值可以指導下一步的維修操作。

4 貝葉斯網絡故障診斷在RIE維修中的應用

刻蝕工藝在半導體工藝中所起的作用越來越大。刻蝕技術分為干法刻蝕和濕法刻蝕，其中干法刻蝕憑借其均勻性好，控制精度高等優點，被廣泛采用。干法刻蝕技術主要有反應離子刻蝕（RIE）和感應耦合等離子體刻蝕（ICP）。本文以RIE刻蝕機為例，介紹一下貝葉斯網絡故障診斷技術在半導體設備故障診斷中的應用。

RIE主要由以下幾部分構成：真空系統，反應氣體及控制系統，射頻電源，匹配網絡等。在RIE的維修中，最常見的故障是設備無法起輝，無法產生等離子體。引起此故障的原因很多：反應氣體的進氣量、真空室的真空度、射頻電源、匹配網絡、腔體的潔凈度等。各個原因之間關系錯綜復雜，給維修帶來了很大的麻煩。利用貝葉斯網絡故障診斷技術，可以將這些故障原因圖形化，并利用這些圖形結構以及各個故障之間的條件概率，計算各個故障原因的概率。

4.1 貝葉斯網絡的構建

通過分析引起此次故障的可能的原因，以及各個原因之間的聯系，確定網絡中的節點類型以及節點之間的聯系。再給定各個節點的條件概率表。這通常是個復雜的過程，為了確保貝葉斯網絡的精確性，可以咨詢領域內經驗豐富的專家，再結合設備的具體情況以及設備的歷史資料等來綜合確定。圖3是RIE無法起輝的貝葉斯網絡結構圖。條件概率表由于比較復雜不再列出。

4.2 貝葉斯網絡的診斷過程

在圖3中可以看出，里面包含很多個節點，每個節點之間的關系錯綜復雜。要計算各個節點的后驗概率是個復雜和困難的過程。結構越復雜，節點越多，運算越復雜。

為解決這個問題，一些科研機構和公司開發了一些貝葉斯網絡的開發工具，本文中所用的工具是Hugin Expert軟件，這是一款基于貝葉斯網絡的分析決策軟件。本文中貝葉斯網絡的構建及運算都是利用這個軟件完成。

圖3 RIE無法起輝的貝葉斯網絡

貝葉斯網絡在進行故障診斷時，各個節點的概率會隨著證據的加入而發生變化，需要根據在取得證據后的概率，進行下一步的操作。圖4列出了各個節點的概率值，圖中所示的是百分數。當前已知的是設備起輝不正常，將這個作為證據，加入到網絡中，經過計算，得出如表1的概率排列。

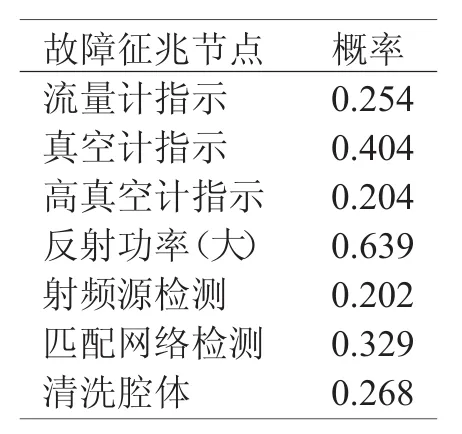
表1 RIE無法起輝下的故障征兆節點概率

如表1所示，此時反射功率大的概率是最大的，檢查反射功率如果反射功率大，將此作為另一個證據輸入到網絡中，重新計算。計算結果如表2

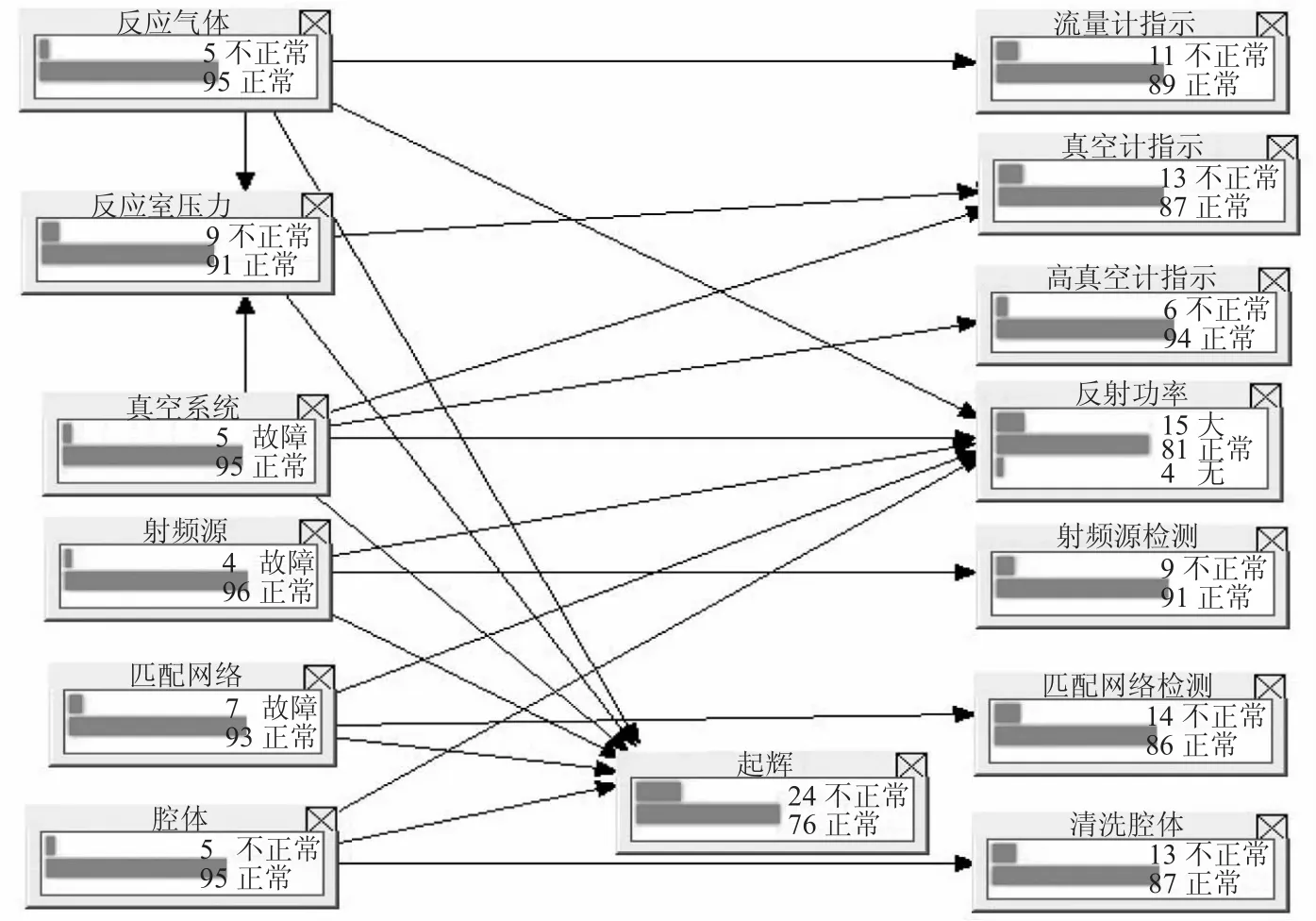
圖4 RIE無法起輝貝葉斯網絡節點的概率

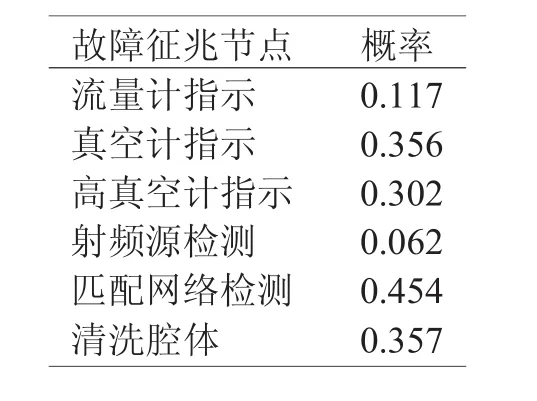
表2 設備不起輝和反射功率偏大條件下征兆節點的概率

通過上述的分析過程可以看出，在RIE的故障檢測中，以貝葉斯網絡計算出的各個節點的概率為指導進行維修，可以減少很多的分析過程，節約大量的時間。設備越復雜，貝葉斯網絡的作用越明顯。

在實際維修中還應該綜合考慮維修成本、維修時間等因素，具體可參看有關文獻[3]，本文不再贅述。

5 結 論

本文介紹了貝葉斯網絡故障診斷技術在RIE刻蝕機維修中的應用，貝葉斯網絡完全可以應用到更復雜系統的故障診斷中。貝葉斯網絡自身還有學習的功能，能將先驗概率的依賴降到最低，提高診斷的精度。故障診斷是貝葉斯網絡的一個應用，貝葉斯網絡還有很多其他的應用，目前被廣泛應用于輔助智能決策、醫療診斷、數據挖掘等領域。

[1] 李儉川，胡蔦慶，秦國軍，溫熙森.貝葉斯網絡及其在設備故障診斷中的應用，中國工程機械，2003，10（5）：896-900.

[2] 張兵利，裴亞輝，貝葉斯網絡故障概述，電腦與信息技術，2008，16（5）:41-42

[3] 趙春華，嚴新平，趙新澤.基于貝葉斯網絡的內燃機故障診斷研究，武漢理工大學學報，2005，29（3）：334-338

[4] Jensen F V，Bayesian Networks and DecisionDiagrams，New York:Springer，2001.

[5] Friedman N，Geiger D，Goldzmidt M.Bayesian Network classifiers[J].Machine Learning，1997，29(2-3):131-163.