基于DSP的實數序列FFT算法探討
郭建濤,范春鳳
(信陽師范學院物理電子工程學院,河南信陽 464000)
“數字信號處理”是電氣信息類學生的一門專業基礎課程,該課程以算法為核心,其特點是理論性強,抽象概念多,對數學基礎要求高,傳統的以教師“單純授課”、學生死記公式的教育模式不僅教學效果差,而且使得學生學習興趣下降,以致今后不愿從事該領域的工作。而“DSP技術及應用”課程重點偏重數字信號處理的實現,學生盡管有濃厚的興趣,但是由于前期的理論基礎有所欠缺,學習“DSP技術及應用”課程時比較吃力,在理論深度、算法設計思想上不能融會貫通,難以達到培養創新能力、實踐能力的根本要求。
傅里葉變換是一種將信號從時域轉變為頻域表示的變換手段,它在信號的頻譜成分分析中起著基礎性的作用。由于快速傅里葉變換(FFT)算法的出現,使得傅里葉變換在信號分析和系統設計中得到了廣泛的應用。DSP技術由于其快速處理大數據量的能力在現代語音、圖像以及視頻應用中得到了快速發展,基于DSP芯片實現FFT算法顯得日益重要。
本文從基本FFT算法理論出發,基于實際應用中信號多為實數數據,給出了實數序列的FFT快速算法,并結合當前通用的TITMS320C54系列DSP芯片,匯編編程實現FFT算法。經過理論分析和實驗仿真,更加有助于加強對FFT算法內容的掌握和理解,大大提高了數字信號處理技術的教學效果。
1 FFT算法基本原理
1.1 N點復數序列的FFT
給定N點復數序列d(n),0≤n≤N-1。為計算方便起見,這里設N=2M,M為正整數。
d(n)的DFT為[1-2]:

將d(n)按照n的奇偶分為兩組,即按n=2r及n=2r+1分為兩組:
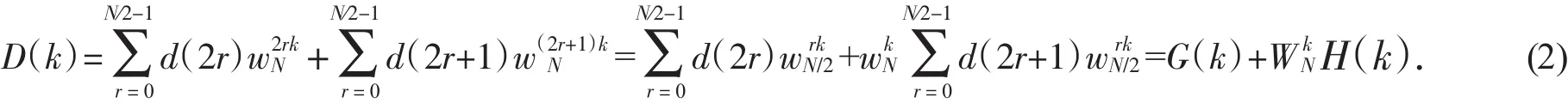
1.2 2N點實數序列的FFT
對于2N 點實數序列 a(n),n=0,1,…,2N-1,按照如下方式構成一N 點復數序列 d(n),n=0,1,…,N-1,a(2n)表示其實部,a(2n+1)是其虛部:
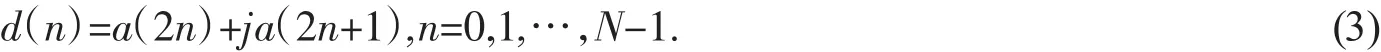
根據DFT的共軛對稱性,知道d(n)的實部的DFT對應于D(k)的共軛偶對稱分量,d(n)的虛部的DFT對應于D(k)的共軛奇對稱分量:

從而得到a(n)的DFT為:

將式(4)代入式(5),得到
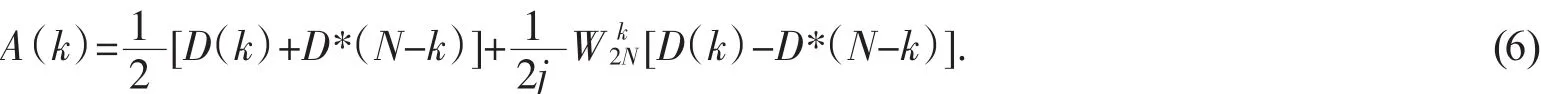
從而,一個2N點的實數序列的傅里葉變換可以通過一個N點復數序列的FFT獲取。
2 FFT的DSP程序實現
下面以2N=256點的實數序列為例說明FFT的DSP實現過程。
2.1 實數FFT運算序列的存儲分配
程序代碼安排在0x3000h開始的存儲器中,其中0x3000h~0x3080h存放中斷向量表,FFT程序使用的正弦表和余弦表數據(.data段)安排在0xc00h開始的地方,長度為0x1400h(分別有256個值),變量(.bss段定義)存放在0x80h開始的地址中。設置256點實數FFT程序的數據緩沖區位于0x2300h~0x23ffh,FFT變換后功率譜的計算結果存放在0x2200h~0x22ffh中[3-4]。
2.2 基2實數FFT運算的算法
該算法主要分為以下2個步驟進行。
第一,輸入數據的組合和位排序。首先,原始輸入的2N=256個點的實數序列復制放到0x2300h開始的相鄰單元,當成N=128點的復數序列d[n],其中奇數地址是d[n]實部,偶數地址是d[n]的虛部。然后,依據圖1輸入數據的排列,把復數序列位倒序后,存儲在以0x2200h開始的數據處理緩沖區中。
程序設計中,使用位倒序尋址方式可以大大提高程序執行的速度和使用存儲器的效率。在這種尋址方式中,AR0存放的整數是實數數據點數的一半(此處僅僅完成位倒序),即128。輸入緩沖指針AR3進行加1減1、位倒序緩沖指針AR2連續加2次,完成一個復數數據倒序。然后按照位倒序尋址方式修改AR3,即,指令:MAR AR3+0B,就可以得到下一數據地址。重復上述過程128次,即可完成輸入數據位的排序工作;這一點通過設置塊重復計數器BRC由RPTB塊重復指令完成[5]。
第二,N點復數FFT運算。在數據處理器里進行N點復數FFT運算。由于在FFT運算中要用到旋轉因子WN,它是一個復數。我們把它分為正弦和余弦部分,用Q15格式將它們存儲在兩個分離的表中。FFT變換關鍵運算主要包括蝶形結個數和單個蝶形結計算兩個部分。
(1)級、組和蝶形結的個數變量及其調整
N點復數序列FFT運算的分成M級,每一級分別進行2,22,…,2M點的FFT運算,此時每一級的組數分別為2M-1,2M-2,…,1,每一級各組中的蝶形結的數目相同,不同級的蝶形結數目分布為20,21,…,2M-1(FFT運算點數的一半)。因此,算法首先制定級、組和蝶形結三個計數器,通過三層循環分別完成各級、各組合單個蝶形結的運算。
計算時,由2個數據指針PX、QX分別指向參加蝶形運算的第一個數據和第二個數據。其中,第二個數據需要乘以旋轉因子(通過指向正余弦表的指針AR4、AR5完成定位)。
(2)蝶形結運算
設定參加蝶形結運算的兩個輸入數據分別為P、Q,包括數據的實部和虛部,用(PR、PI)和(QR、QI)表示;輸出分別 P′,Q′,旋轉因子用 W 表示,相應的實部和虛部表示用其后添加R和I加以明示,見圖1。
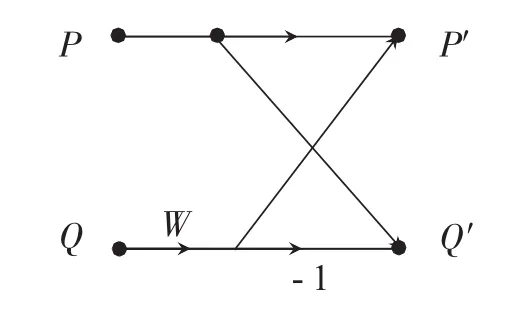
圖1 單個蝶形運算
對于旋轉因子W,正余弦表格給出的僅僅是正余弦值,用Q15格式將它們存儲在兩個分離的表中。每個表中有128項,對應0°~180°。因為采用循環尋址地址來對表尋址,128=27<28,因此每張表排隊的開始地址就必須是8個LSB位為0的地址。按照系統的存儲器配置,把正弦表第一項“sine_table”放在0x0C00的位置,余弦表第一項“cos-table”放在0x0D00的位置。
在計算蝶形輸出時相應的實部是用減法,虛部用加法,即
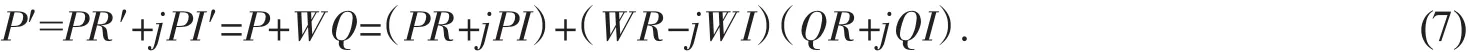
因此,蝶形結第一個輸出數據的實部表示為PR′=PR+QR×WR+QI×WI,第一個輸出數據的虛部表示為PI′=PI+QI×WR-QR×WI。同樣可得到蝶形結第二個輸出數據的表示形式,這里不再給出[6]。相應的關鍵匯編指令如下:

其中,第二個數據與系數相乘后,所得結果是32位數,與第一個數據的實部相加時,需要將該實部數據左移16位后執行;并行指令可以在一個指令周期內,將B高端移位ASM,存于AR2所指定的存儲單元中,并執行將AR2所指的單元中的值左移16位后減去累加器B的值;在實際編程時,為了避免溢出,對每一步的輸出右移一位(相當于將結果除以2,相當于把的比例因子分散到各級運算之中,可以在保持輸出信號方差不變、輸出信號最大幅度等于輸入值N倍的情況下,減小輸出噪聲電平,增加輸入信號幅度)。應該指出,在FFT的各級運算過程中,相應的中間結果、FFT輸出和整理后的結果都存儲在該緩沖區中,從而實現原位計算。
第三,產生輸出結果。這里將D(k)重新表示為實部和虛部的形式[7]:
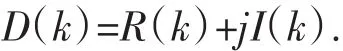
代入式(6)可以得到2N點實數序列的DFT表示式:
A(k)=AR(k)+jAI(k)
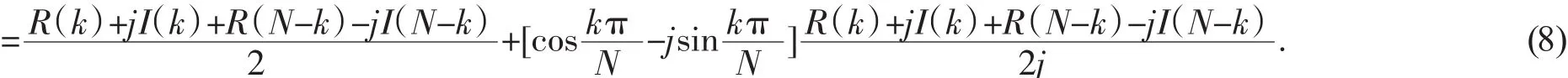
從而有
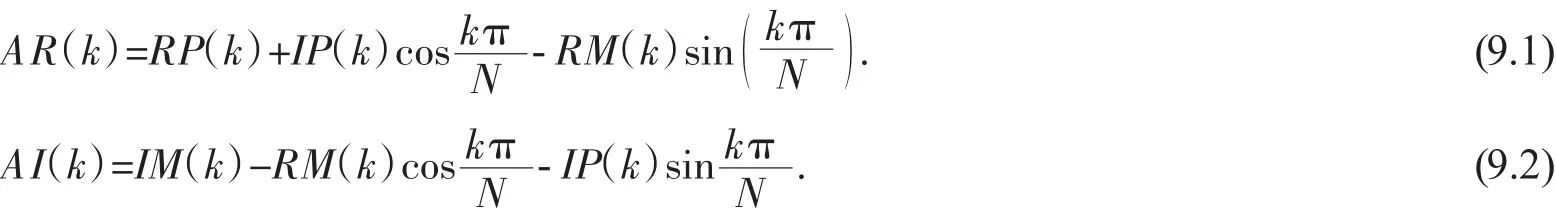
其中,RP(k)和 IP(k)分別表示 D(k)的偶對稱部分的實部和虛部,RM(k)和 IM(k)分別表示 D(k)的奇對稱部分的實部和虛部,即


編程時首先實現輸出復數序列的奇偶分解,求解RP(k)、IP(k)、RM(k)和IM(k)。這一點通過4個指針分別指向R(k)、R(N-k)、I(k)和I(N-k),然后完成式(10)的計算。程序最后按照原始序列的DFT對上述結果按照式(9)計算,并以自然順序存儲在整個4N長的數據緩沖區內。
3 實驗結果與分析
給定包含兩個頻率分別為5Hz、10Hz正弦信號,采樣頻率200Hz,取數據長度為256。將Matlab生成的信號源文件轉換為CCS能夠識別的.dat格式,這里命名為input.dat文件。在CCS中,首先設置探針斷點Toggle Probe point,從File菜單項中選擇File I/O,在出現的窗口中選擇輸入文件input.dat。單擊Add Probe Point,出現探針斷點窗口下,將輸入文件與設置的探測點連接起來。根據公式(3)將a(n)組合為復數序列d(n),經過128點的FFT后得到其傅里葉變換D(k),并順序存放在0x2200h-0x23ffh的緩沖區中,前半部分為d(n)、后半部分為D(k),如圖2。由于復數的實部和虛部分開存放,因此一共占用512個字長。圖3是256點實數序列a(n)的傅里葉變換A(k),頻譜關于零頻對稱,相應的功率譜顯示在圖4中,與A(k)不同的是,功率譜僅有256點。為了比較起見,圖5給出了利用Matlab軟件計算得到的實數序列a(n)的功率譜結果,與圖4相比較,可知DSP算法匯編程序給出了信號正確的傅里葉變換結果。

圖2 D(k)和輸入信號
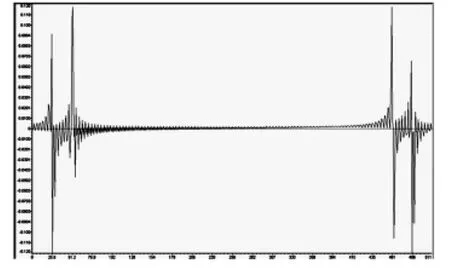
圖3 實數序列的FFT
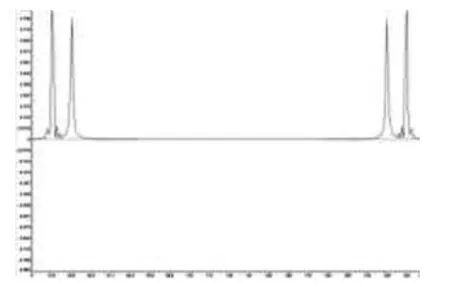
圖4 信號功率譜(ccs)
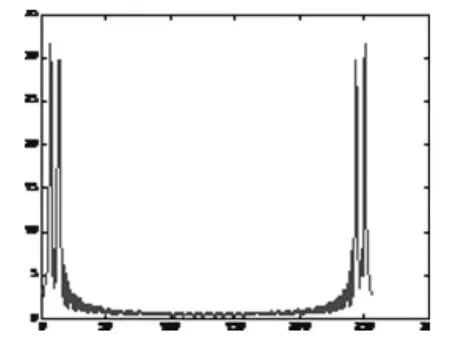
圖5 信號功率譜(Matlab)
4 結論
2N點實數序列可以用N點FFT算法實現,實驗證明,在TMS320VC5416定點DSP中運行結果正確。同樣該程序經過簡單的參數修改可以適用于其它點數的信號傅里葉變換,并應用于實際系統中。這種從理論到實現的流程教學方法,不僅增強了實際的教學效果,也有助于培養學生的工程實踐和創新能力。
[1]吳鎮揚.數字信號處理[M].北京:高等教育出版社,2004.
[2]陳佩青.數字信號處理教程[M].北京:清華大學出版社,2007.
[3]趙宏怡.DSP技術與應用實例[M].北京:電子工業出版社,2008.
[4]陳金鷹.DSP技術及應用[M].北京:機械工業出版社,2011.
[5]劉和平.TMS320C240xDSP C語言開發應用[M].北京:北京航空航天大學出版社,2003.
[6]邱立存,聞武,劉海英.TMS320C54X系列DSP上FFT運算的實現[J].微計算機信息,2005(7):136-137.
[7]肖宛昂.嵌入式系統中FFT算法研究[J].單片機與嵌入式系統應用,2003(4):68-69.

