基于隨機過程的設備性能可靠性預測

莫協強

由于在現實生產生活中各行各業各種事物都具有一定的空間形式和數量關系，所以這種敏感不僅局限在數學思維品質，而且屬于社會行為品質了，它的表現形式努力使外界現象數學化，注意現象的數學方面，注意空間和數量關系以及函數間的依賴關系。特別是對于隨機過程的分布函數來說，其在生產生活的應用非常廣泛，例如，在工業工程中設備性能的可靠性預測和故障排除方面的應用。以下將結合實踐中的設備性能可靠性預測與隨機過程的分布函數之間的關聯性進行闡述[1]。

一、隨機過程的概述

（一）隨機過程的概念

在許多實際問題和工程中，我們不僅需要研究一個或幾個變量，而且還要研究一族無限多個隨機變量，例如，為描述系統的隨機運動或工程中隨機現象的變化過程，我們必須引進依賴于時間參數的隨機變化量，也就是依賴于時間參數的一族隨機變量，這就產生了隨機過程這一概念，例如，以X（t）表示某電氣監測裝置在累積開機時間(0，t)內出現的故障數，對于每一個固定的時刻t(t＞0)，X(t)是一個取非負整數值0，1，2，……的隨機變量，隨著t的變動，得到了一族無窮多個相互有關的，且均依賴于時間 t的隨機變量 X（t）(t＞0)，X（t）即為隨機變量。又如，設某一運用中的電氣設備在任一時刻只能于正常、異常和故障三種狀態之一，分別記為2，1，0，若以Y（t）(t≥0)，表示在t時刻系統所處的狀態，則對任意固定的t≥0，y(t)是一個只能取 0，1，2三個值的隨機變量，而隨機變量族y(t)(t≥0)就描述了該設備在運用中整個過程，Y（t）即為一隨機過程[2]。

（二）隨機過程的統計描述

隨機過程在任一時刻的狀態是隨機變量，因此，可以用隨機變量的統計表述方法來表述隨機過程的統計特性。以下是隨機過程的分布函數族。

給定隨機過程{X(t),t∈T}，對于每一個固定的t∈T，隨機變量X（t）的分而函數一般與t有關，記為

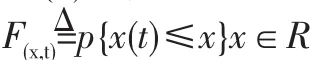
稱為隨機過程{X(t),t∈T}的一維分布函數，而{F(x,t),t∈T}為一維分布函數族。 一般地，對 n(n=2,3,L)個不同時刻，t1，t2，t3,Ltn∈T引入n維隨機變量{x(t1),x(t2),L,x(tn)}，它的分布函數記為

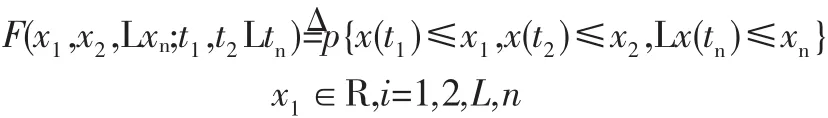
我們稱{F(x1,x2,Lxn;t1,t2,Lxn),t∈T}為隨機過程{X(t),t∈T}的n維分布函數。

當n取方充分大時，n維分布函數族能夠近似地描述隨機過程的統計特性，n取愈大，則n維分布函數族描述隨機過程的特性愈趨完善[3]。

二、基于隨機過程的設備性能可靠性預測

（一）馬爾可夫過程

有很多工程現象遵從如下演變原則：由時刻系統或過程所處狀態，可以決定該系統或過程在時刻t=t0。所處的狀態，而無需借助于以前系統或過程所處狀態的歷史資料。例如，電力設備的運行狀態(用可靠度來描述)，如果只與上次設備的修理狀態有關，而與更前面幾次設備的修理狀態無關。又如研究某設備的絕緣特性，如果現在時刻的某絕緣特性指標已知，則未來某一時刻的該絕緣特性與現在的絕緣特性指標有關，而與這之前的任一時刻的絕緣特性情況無關等等。這就是統計規律上所說的無后效性。用更通俗的話說就是已經知道過程“現在”的條件下，其“將來”不依賴于“過去”。這種已知時刻t系統所處的狀態下，在時刻t以后，系統的變化情況與以前系統所處的狀態無關的隨機過程稱為馬爾可夫過程[4]。

設隨機過程{X(t),t∈T}的狀態空間為I，如果對時間t的任意 n 個數值 t1＜t2＜L＜tn，n≥3,ti∈T， 在條件 X(ti)=xi，xi∈I，i=1，2，Ln-1 下，X(tn)的條件分布函數恰等于在條件 X（tn-1）=xn-1下 X（tn）的條件分布函數，即

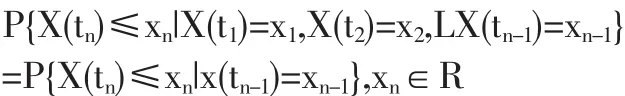
當n=1，即由ai狀態經過一步轉移到aj狀態的概率為一步轉移概率。

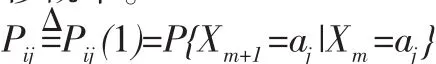
例如，討論單設備維修系統的轉移概率，這是個最簡單的維修系統，設X（t）表示時刻t系統所處的狀態，當設備工作時，系統處于工作狀態即X（t）=0，當設備發生故障時，系統牌故障狀態，即。

系統從t=0時刻開始工作，經一段時刻發生故障，系統即處于故障修理時刻，經一定時刻設備修復后又立即投入正常工作狀態，如此形成故障與工作狀態不斷交替進行，顯然是{X(t),t≥0}是一個隨機過程，即設備在正常與故障的相互狀態轉移過程只與現在所處的狀態有關，而與以前的狀態轉移無關，這過程是一個時間連續，狀態空間有限a={0，1}即的馬爾可夫過程[5]。

若討論設備的故障分布服從指數分布，因此系統的狀態轉移概率只與狀態 a{0，1}和時間的間距 Δt有關，因而{X(t),t＞0}是一個齊次馬爾可夫過程。設系統的壽命θ和維修時間η分別服從如下分布

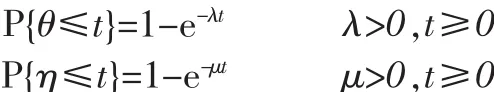
且設備修復與新的一樣的壽命分布，和相互獨立。

例如，對于某設備組成各部分和安全裝置的安全要求以及安全信息的順利傳遞來實現的。設備的基本使用功能是在建筑物內垂直升降運輸人員和物料。這是由設備合理的結構形式和各組成零件、部件具有足夠的機械強度來保證的，即在額定滿載情況下，考慮全部靜載荷、動載荷，以及意外情況采用緊急措施所產生的載荷作用，不應發生破壞。因此在這種狀態下應用隨機過程的分布函數可以得出如下的模型，即在設備的可靠性預測當中，要將設“0”表示系統處于正常狀態，“1”表示系統處于故障狀態；P00表示系統保持于正常狀態的概率；P01表示系統從正常狀態向故障狀態轉移的概率；P10表示系統從故障狀態向正常狀態轉移的概率；P11表示系統保持在故障狀態的概率[6]。

上世紀20年代，在美國首先實行了預防性的定時維修，即在設備運行，使用到某周期之后，就對設備進行拆卸檢查，更換部分零部件，以此預防設備故障的發生。這種防患于未然的定時維修方法減少了設備故障和生產中事故的發生，提高了企業的生產效益。這種維修方法，顯然優于那種“不壞不修，壞了才修”的事后維修方法。因此這種定時維修方法的明顯優點和產生的效益，使得它迅速被世界各地所采用。此時設備的變化情況與之前設備所處的狀態無關的隨機過程就可以用來進行分析。

系統或設備在使用中，主要處于運行使用狀態和因故障的停運進行檢修狀態，這兩種狀態不斷循環，構成了設備整個運行使用過程，我們稱設備的這種工作狀態與停運檢修狀態之間的循環過程為更新狀態，設備每經過一次修理，稱為一次“更新”。隨著設備維修技術的不斷發展，特別是設備群控技術的發展，客觀上要求設備的控制系統精確地了解每臺設備的載荷量，才能使設備的調度運行達到最佳狀態。因此，傳統的開關量載荷信號已經不能適用于群控技術，現在很多設備采用電磁式稱量裝置，為設備控制系統提供連續變化的載荷信號。這樣一方面可以方便群控系統進行調度，另一方面可以將載荷信號傳遞給設備的拖動系統，在設備起動和運行期間調節供給曳引機的電流，調節曳引機的轉矩，保證設備的正常運行。這種維修保護裝置應用非常廣泛、價格低、安全可靠，但更換維修較繁瑣，這是裝在設備上的超載裝置，活動地板四周與設備之間保持一定間隙，隨著設備承受載荷的不同，會微微地上下移動。當設備超載時，會使活動地板下陷，將開關接通，給出設備相應的控制信號。通過眼看、耳聽、觸摸等感觀手段來判斷為主，最多輔以簡單檢測設備(如電工使用萬用表)，進一步判斷、處理和修復故障。此階段維修僅是一門操作技藝，其工作主要目的是排除故障。維修過程缺乏理淪支持，主要是依靠經驗的傳授和積累。顯然這也符合當時設備的工藝水平和生產發展的實際情況。隨著工業化的進步，生產力有了較大的發展，尤其是第一次世界大戰之后，工廠企業生產力大為提高，開始出現了流水線生產和連續性作業，仟何生產線作業中斷，將造成較大的經濟損失[7]。

（二）更新理論

更新理論是研究維修系統的更新過程的一種基本原理和方法，應用于研究零部件的更新，確定維修周期、制定試驗程序等。由一批相同零部件組成的單部件設備的更新過程。該設備從時刻T0=0開始工作，當設備中某一零件故障，就立即換上一個新的，并假定更換后立即工作，故系統可一直繼續不斷地工作。于是，系統中各個零件后發生故障的時間的關系為

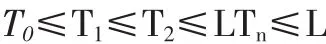
式中，Tn——第n個零件的故障時間，也是第n次更新時間（在此時間內，有n個零件故障并予以更換）。

因此， 第 n 個零部件的壽命 τn=Tn-Tn-1， 這些壽命（τ1，τ2，L，τn）是非負隨機變量，分布相同且相互獨立，第n次更新時間為 τn=τ1+τ2+L+τn

我們稱上述時間序列T0≤T1≤T2≤LTn≤L為更新過程。

若 T0≤t≤Tn+1，則在時間（0，t）之間有 n 個零件故障，設 N(t)表示更新次數，即 N(t)=n，這樣在（0，t）時間內有兩個隨機變量，更新次數N(t)和第n次的更新時間T，前者為有離散型隨機變量，其值為正整數0，1，2，……，后者為連續型隨機變量，其值為任意非實數，所以，在一定的t條件下它們之間的關系，根據概率定義有

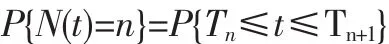
因此設，

式中Fn(t)為故障率F(t)的n次卷積。

預防性維修通常是對設備進行檢查、測試，在發現異常或故障時予以消除，防止事故、故障的發生，使設備保持在規定的狀態下所做的各項維修活動。預防性維修工作一般包括外觀檢查，清潔，機械部分的潤滑和調整，電氣部分的測試和調整，裝置的拆修及不合格元部件的更換等。預防性維修活動的企圖是消除故障的隱患，確保設備在運行使用過程中不發生故障，從而避免造成更大的損失，做到防患于未然。其活動的時機是在故障發生之前進行，這種維修方法一般用于故障后果會危及安全或影響功能的實現和任務的完成，或者故障會造成較大經濟損失和社會影響。

[1]蘇文勝，蘇永共.灰色─馬爾柯夫模型在接發列車事故預測中的應用研究[J].中國安全科學學報，1996，（11）

[2]謝賢平，李懷宇，趙梓成.事故預測專家系統（AFES）的設計[J].勞動保護科學技術，1994，(6)

[3]王賢.“引火燒身”及其它設備內部安全動火[J].勞動保護，1994，（11）

[4]顏炳發.淺談化工工藝和設備安全性評價[J].黑龍江科技信息，2011，(17)

[5]路立軍.淺談化工設備檢修中的動火安全措施[J].設備管理與維修，2000，(11)

[6]郭建波，趙勇，齊照東.鐵路事故研究現狀及應用[J].工業安全與環保，2005，(3)

[7]黃鄭華，李建華，華楊.化工設備檢修中的火災爆炸事故原因分析[J].安全、健康和環境，2005，(12)