基于參數化雙譜分析的超寬帶生物雷達人體目標非接觸檢測

劉淼，呂昊，李盛，荊西京，王健琪

第四軍醫大學 生物醫學工程學院，陜西 西安 710032

基于參數化雙譜分析的超寬帶生物雷達人體目標非接觸檢測

劉淼，呂昊，李盛，荊西京，王健琪

第四軍醫大學 生物醫學工程學院，陜西 西安 710032

超寬帶（Ultra Wideband, UWB）生物雷達廣泛應用于生命體探測等領域，而人體生命體征信息的非接觸檢測是其需要解決的最主要問題。本文利用參數化雙譜估計算法分析UWB生物雷達回波信號，以非高斯白噪聲激勵的AR（Auto Regression）參數模型對信號進行建模，并用帶約束的三階平均法對模型的參數進行估計。在此基礎上，提出了一種新的基于UWB的人體目標非接觸檢測算法，并將該算法與現行的基于功率譜密度的檢測算法進行對比。實驗結果表明，有人位置點信號和無人位置點信號在雙譜域表現出明顯的差別特性，新算法能更好地實現人體目標的非接觸檢測。

目標探測；UWB雷達；非接觸；AR模型；雙譜分析法

0 前言

超寬帶（Ultra Wideband, UWB）生物雷達具有高分辨率且其發射的電磁波可穿透非金屬物質，因此在震后人員搜救和反恐等多個領域發揮了重大作用。不同國家的多個課題組都致力于 UWB 生物雷達的研究[1]。奧地利的 G. Ossberger 采用小波變換的方法對雷達回波信號進行分析，該方法能探測到自由空間條件下距離雷達 5 m 及穿透厚度為 20 cm 的磚墻距離雷達 0.85 m 的呼吸信號[2]，但此方法依賴于母小波的選擇。西班牙的 A. Lazaro 等人對 UWB雷達探測到的人體重要生理信號進行分析，并對呼吸率和心跳頻 率 進行估計[3]；第四軍醫 大學李巖 峰等人采用 自適應抵消的方法實現了兩個人體目標的探測[4]，這些研究中使用的生命特征非接觸檢測算法主要是基于功率譜密度（Power Spectral Density, PSD）的。根據維納辛欽定理，寬平穩隨機過程的功率譜密度是其自相關函數的傅里葉變換，因此該方法實質上是建立在二階統計量基礎上的。但是，從應用的角度來說，生物醫學信號一般為非平穩隨機信號。另外，UWB生物雷達的目標探測主要依靠探測人體呼吸信號，而呼吸信號作為一種準周期信號，是非高斯信號的一種。對UWB生物雷達回波這種非高斯非平穩信號采用基于功率譜密度這種二階統計方法會丟失重要信息以及引入估計誤差。此外，實際應用中，雷達目標所處環境復雜，回波中不可避免的伴有噪聲和雜波，采用基于功率譜密度的方法難以消除雜波和噪聲的影響。

高階譜估計算法在分析非高斯非平穩隨機信號方面有很大的優勢，它定義為相應高階累積量的多維傅里葉變換，其不僅可以提供信號的高階信息，還包含有信號的相位信息，可以更好地反映這類信號的特征。更重要的是，高斯白噪聲在高階譜域是恒為0的，這為去除回波信號中的噪聲及雜波提供了重要途徑。雙譜分析作為高階譜分析中最簡單、階次最低的分析方法得到廣泛應用[5-6]。

本文利用參數化雙譜估計算法對UWB生物雷達回波信號進行分析，找到了一種性能優良的人體目標非接觸檢測算法。

1 實驗平臺及數據獲取

本 實 驗 平臺采用中心頻率為 400 MHz，帶寬為 400 MHz的 IR-UWB 體制生物雷達系統，滿足 FCC 對超寬帶的定義[7]。雷達發射的電磁波到達人體表面，由于呼吸等生理活動引起人體體表微動，回波信號即攜帶重要的人體生命體征信息。雷達回波信號經 A/D 轉換器以二維信號的形式存儲在計算機存儲介質中。沿著雷達徑向距離方向（也被定義為快時間方向）的每道波形包含有 4096 個采樣點，由 于 雷 達 的 脈 沖 重 復 頻 率（Pulse Repetition Frequency, PRF）為 250 kHz，沿著時間方向（也被定義為慢時間方向）的采樣頻率則約為 60 Hz，人體呼吸信號大部分在 0.2～0.5 Hz范圍內，因此對雷達回波信號的采樣滿足奈奎斯特采樣定理。

具體實驗方法，見圖 1。受試者位于一堵 24 cm 厚的磚墻后 3 m 的位置，雷達則緊貼墻面置于墻體另一側。一臺PC 通過 Wi-Fi信號與雷達連接對雷達進行參數設置并實現數據存儲功能。

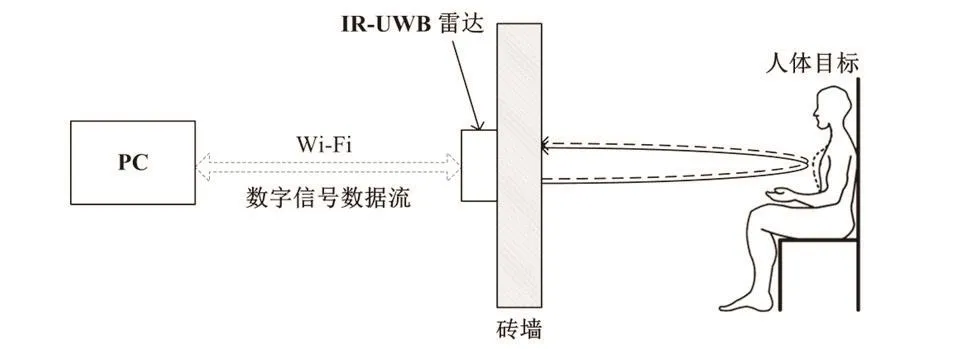
圖1 IR-UWB雷達探人實驗系統示意圖

2 參數化雙譜算法分析UWB生物雷達信號

2.1 雙譜估計算法簡介

設實隨機序列x(n)的均值為零 ,其三階累積量表示為

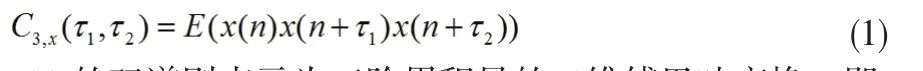
x(n)的雙譜則表示為三階累積量的二維傅里葉變換，即

雙譜還可以由下式給出：

雙譜具有很多優良的性能。首先，理論上，在雙譜域高斯信號恒為0，即雙譜對于高斯隨機過程是盲的。本文即是利用了雙譜對高斯噪聲的消除作用來更好地達到探測目的。另外，雙譜具有極強的對稱性，有12個對稱區域。其對稱特性表現，見圖 2，三角形主值區域 OAB 內的值即可完整描述整個區域的雙譜值[5]。

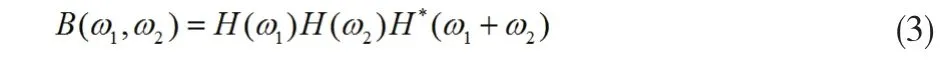
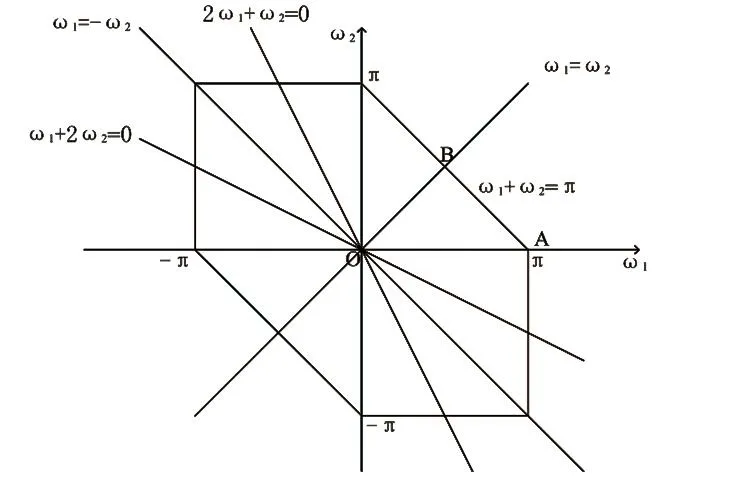
圖2 雙譜的對稱性

2.2 非高斯AR模型參數化的雙譜分析

基于 FFT 和加窗技術的雙譜估計算法，在數據較短的情況下，估計誤差會比較大,分辨率較低。因此，以非高斯白噪聲激勵的AR參數模型對信號進行建模，并用帶約束的三階平均法對模型的參數進行估計。

設零均值回波信號 x(n)由以下 p 階非高斯 AR 模型表示：

其中w(n)是均值為零的非高斯白噪聲，而且滿足下列條件：

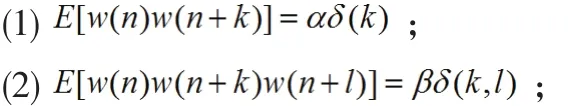
(3) 當 m＜n 時，x(m)與 w(n)相互獨立。

定義

根據相關參考文獻[6]，可得到

以矩陣的形式表示：

其中，

其中，

以上討論的非高斯AR建模過程中，假定模型的階次是已知的。實際上，在進行參數化雙譜估計時必須考慮模型階次的選擇。許多用于參數化譜估計的AR模型定階準則只涉及二階矩，因此不能作為選擇模型的階次的依據。而奇異值分解方法和信息論準則等在階次較高時性能不佳。針對這一情況，本文采用雙譜互相關系數估計非高斯AR模型的階次[8]，具體方法不再贅述。

2.3 參數化雙譜估計對UWB生物雷達信號處理

2.3.1 有人和無人位置點信號的雙譜分析

此分析的目的是為觀察有人位置點信號和無人位置點信號在雙譜域上的差別。因為雷達發射的UWB信號要穿透墻壁，而且電磁波的傳播速度受空氣濕度等因素影響較大，目標位置點信息并不是與目標所在位置的物理參數成簡單線性比例關系。為確定目標所在的確切位置點信息，實驗采用課題組前期研制的模擬人體系統生命信號發生 器[9]， 將 其 置 于 雷 達 后 3 m 的 位 置 ， 分 別 采 用 基 于 能量累加和基于過零點的檢測方法探測人體目標位置，并將兩種方法探得的各點信息平均，即可作為雷達所探測的點位置信息。實測實驗中，受試者立于相同的位置，提取出目標所在位置點信號和距離此位置較遠的點信號，并分別做雙譜分析。

2.3.2 基于參數化雙譜估計的UWB生物雷達人體目標非接觸檢測算法

具體的基于參數化雙譜估計的UWB生物雷達人體目標非接觸檢測算法實現流程，見圖3。

圖3 基于CTOM法參數化雙譜估計的人體目標非接觸檢測算法流程圖

為了減少計算量和增大信噪比，原始數據要進行距離累積，每道信號由原來的 4096 點減至 200 點。具體對每點信號進行雙譜估計為：將數據分成M段，對中心化后的每組序列估計為 qij，將所估計的 M 個qij平均以減少估計誤差。將平均后得到的qij代入公式 (9)得到 AR 模型的 參數，再根據 (10)式即可得到雙譜值。

正如 2.1 中討論，雙譜具有很強的對稱性，為了在保存所有信息量的條件下減小計算量，僅將主值區域內的雙譜值進行累加。累加后所得值作為代表該位置點信號的參數，累加值最大處即被認為目標所在位置。

將提出的新方法與現行的基于功率譜密度的方法進行對比，基于功率譜密度的方法具體參見相關參考文獻[10]。其實現流程見圖 4 。

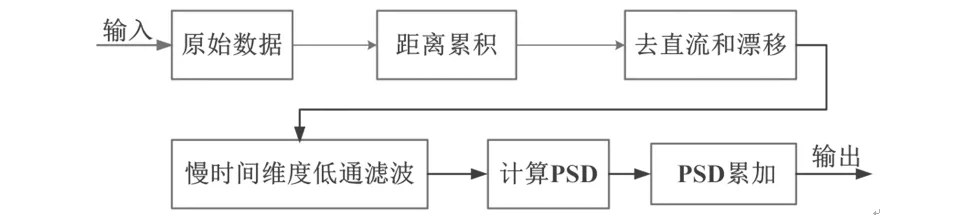
圖4 基于PSD的UWB生物雷達人體目標非接觸檢測算法流程圖

3 實驗結果及分析

3.1 有人和無人位置點信號的雙譜分析

將模擬人體系統生命信號發生器置于雷達后 3 m 的位置，分別采用基于能量和基于過零點的檢測方法探測人體目標位置，探測結果皆位于距離累積后 200 點中的 107 點，故確定當真實人體目標位于此位置時，自動探測結果應在107 點附近。實驗中則以 107 點位置的點信號作為有人點位置信號，選擇距離此位置較遠的 60點位置的點信號作為無人點位置信號。

圖 5、圖 6分別為有人位置點和無人位置點信號的歸一化雙譜圖。不同于具有明確的物理意義的功率譜，雙譜的物理意義并不明確。根據相關參考文獻[11]，雙譜域上的幅值可理解為信號的偏態在雙譜域上的分解。根據結果圖可知，有人位置點信號的偏態基本存在于低頻區域，此現象是由于人體呼吸信號引起的。而無人位置點信號的偏態則廣泛分布于整個雙譜區域，盡管理論上高斯信號在雙譜域為0，但實際應用中，回波信號不可能僅受到高斯噪聲影響，故雙譜表現出此種特點。因此，有人位置點信號和無人位置點信號的雙譜有明顯的區別。

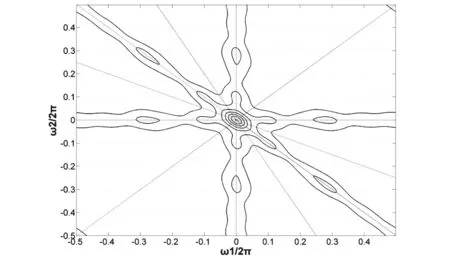
圖5 有人位置點信號歸一化雙譜圖

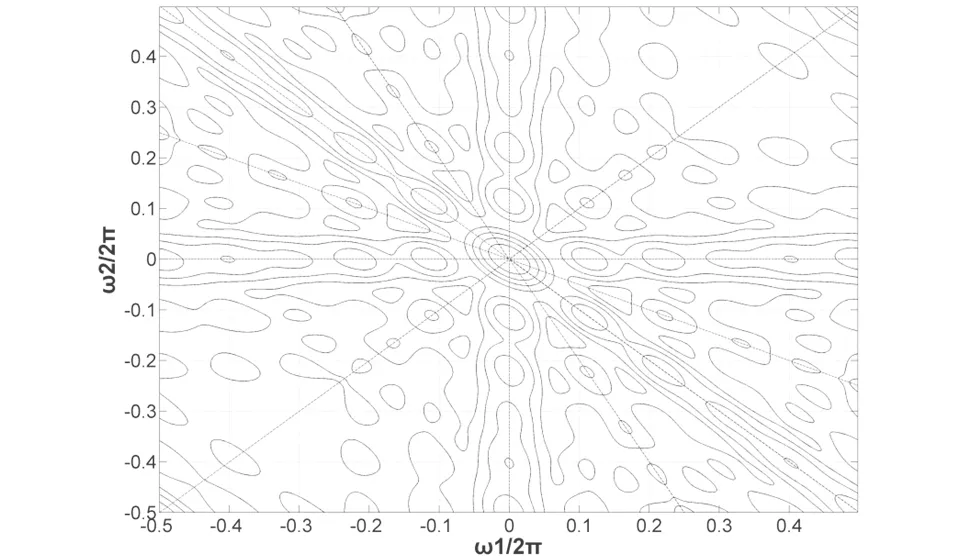
圖6 無人位置點信號歸一化雙譜圖

3.2 基于參數化雙譜估計的UWB生物雷達人體目標非接觸檢測算法

圖7、圖8分別為兩種算法所得的結果。在兩種方法中，人體目標均引起一定區域的幅值增大，而最大值出現處則自動判別為目標所在位置。兩種方法均可探得人體目標所在位置。然而，基于參數化的雙譜估計算法則對非目標所在區域的抑制作用更為明顯。定義參數K為人體目標引起幅值增大區域的最大值除以非目標區域的最大值。K值越大，非目標區域對自動探測目標所在位置的影響越小。由實驗結果可知，基于參數化雙譜估計算法的K 值可達30左 右 ；而基于 PSD 算法 的 K 值僅能達到 3 或 4，這 種現象預示此種方法更容易發生誤判。此外，基于參數化雙譜估計算法中，目標引起的幅值增大區域范圍小于基于 PSD算法的幅值增大區。這意味著前者所探測的位置信息將會更為準確。另外，這種優良的性能也有助于多目標的識別探測，即當兩個目標距離較近時，不易發生混疊現象，而混疊現象容易導致分不清是由幾個目標引起的幅值增大。

由此可見，基于參數化的雙譜估計算法具有比基于PSD 算法更好的性能。基于功率譜密度的算法需要在較高信噪比的情況下才適用，然而實際雷達操作中，由于呼吸信號本身微弱再加上應用環境復雜和電磁波衰減，導致實際信噪比不能達到很高的水平，因此頻率累加區域中噪聲成分也會被當作有用信號進行累加。理論上，準確估計呼吸信號的頻率可以縮小累加的頻率區間，進而減少無用噪聲被當作有用信號。但是，缺少先驗知識以及人體呼吸信號頻率的不穩定性和個體差異使得該方法難以實現。而雙譜在本質上對高斯噪聲就是盲的，從而從根本上杜絕了噪聲信號被累加。

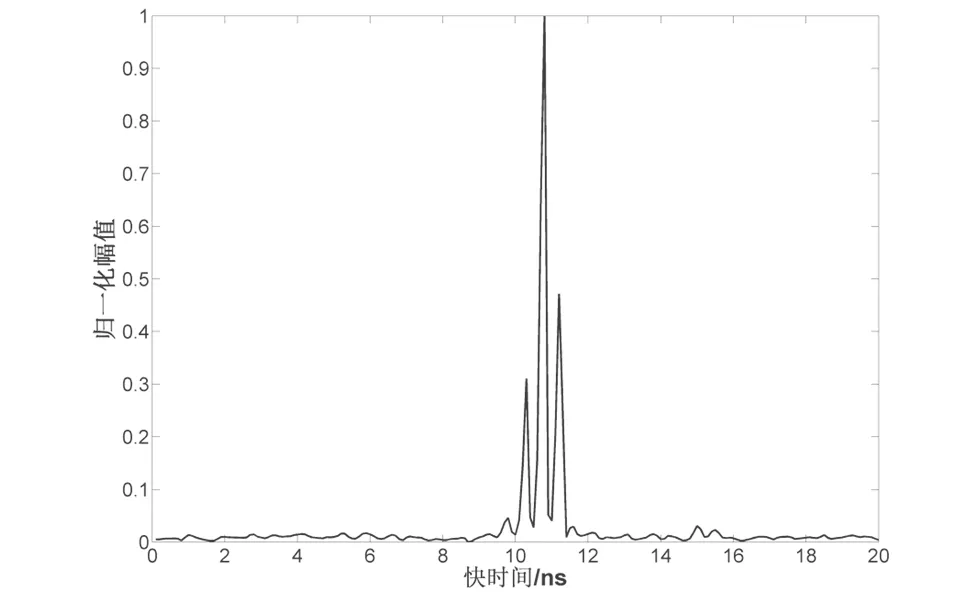
圖7 基于參數化雙譜估計算法所得結果

圖8 基于PSD算法所得結果

4 結論

本文采用基于參數化的雙譜估計算法對UWB回波信號進行分析，實驗結果顯示，有人和無人位置點信號的雙譜有明顯區別。另外，利用雙譜可以抑制高斯噪聲的特點，提出一種新的基于UWB生物雷達非接觸人體目標檢測算法，并與基于功率譜密度的算法進行比較。實驗證明，新提出的算法具有更優良的性能。然而，新方法的不足之處在于運算速度較慢，這也是影響雙譜廣泛應用的一大原因。下一步工作是尋找簡化的雙譜算法，盡量減少運算量，提高運算速度。

[1] Aardal ?,J Hammerstad．Medical radar literature overview[R]．Norway,Norwegian Defence Research Establishment,2010．

[2] Ossberger G,Buchegger T,Schimback E,et al．Non-invasive respiratory movement detection and monitoring of hidden humans using ultra wideband pulse radar[A]．Joint UWBST & IWUWBS．2004 International Workshop on[C]．2004,395-399．

[3] Lazaro A,D Girbau,R Villarino．Analysis of vital signs monitoringusing an IR-UWB radar[J]．Progress In Electromagnetics Research,2010,100(1):265-284．

[4] Li Y F,Jing X J,Lv H,et al．Analysis of characteristics of two close stationary human targets detected by impulse radio UWB radar[J]．Progress In Electromagnetics Research,2012,126:429-447．

[5] Nikias CL,MR Raghuveer．Bispectrum estimation: a digital signal processing framework[J]．Proceedings of the IEEE,1987,75(7):869-891．

[6] Raghuveer M,C Nikias．Bispectrum estimation: a parametric approach[A]．Acoustics,Speech and Signal Processing,IEEE Transactions on[C]．1985．33(5):1213-1230．

[7] Oppermann I,M H?m?l?inen,J Iinatti．UWB:theory and applications[M]．Jhon Wiley&Sons,2004．

[8] 劉毅,張彩明,馮峰,等．基于高階累積量的參數化雙譜分析的肺音特征提取[J]．山東大學學報(工學版),2005,35(2):77-85．

[9] 呂昊,王健琪,荊西京,等．模擬人體系統中生命信號發生器的研究[J]．醫療衛生裝備,2006,27(9):11-12．

[10] 倪安勝,王健琪,楊國勝．基于FFT頻域積累的非接觸生命參數信號檢測[J]．第四軍醫大學學報,2003,24(2):172-175．

[11] 陳濤,姚文楊,翟孝霏,等．雷達輻射源信號雙譜估計的物理意義及其輻射源個體識別[J]．中南大學學報(自然科學版),2013, 44(1):179-187．

Non-contact Detection of Human Targets via UWB Bioradar Based on Parametric Bispectrum Analysis

LIU Miao, LV Hao, LI Sheng, JING Xi-jing, WANG Jian-qi
School of Biomedical Engineering, The Fourth Military Medical University, Xi’an Shaanxi 710032, China

Ultra Wideband (UWB) radar has been widely used in many areas such as life detection and so on. One of the most concerned problems should be solved through UWB radar is the non-contact detection of vital signs information for human. In this paper, a parametric bispectrum estimation algorithm was applied to analyze the UWB echoes and an autoregressive (AR) model driven by non-Gaussian white noise was applied to finish the signal modeling. Then estimate the parameters with the constrained third order mean (CTOM) method. Thus, a novel detection algorithm for human targets based on the UWB radar was developed. Then compare this algorithm with a detection algorithm based on power spectrum density (PSD). Comparison results showed that there was significant difference between signals of positions with human targets and signals of positions without human targets within bispectrum domain, which indicated that new algorithm can implement the non-contact detection for human targets effectively.

human detection; UWB radar; non-contact; AR model; bispectrum

R318.04；R197.39

A

10.3969/j.issn.1674-1633.2013.11.005

1674-1633(2013)11-0015-04

2013-09-05

國家自然科學基金項目(61201382)；陜西省國際合作

重點項目（2013KW30-03）；陜西省自然科學基礎研究計劃項目（2012JQ8022）。

本文作者：劉淼，碩士研究生，主要研究方向為非接觸生命信號檢測。

王健琪，教授，博士生導師。

作者郵箱：lium90@163．com