城市景觀林中幼齡期紅錐個體大小之統計分布模型

殷祚云，曾令海，何波祥，連輝明，張謙，蔡燕靈，陳一群，藍燕群

廣東省林業科學研究院，廣東 廣州 510520

紅錐Castanopsis hystrix A. DC.是南亞熱帶地區珍貴、優良的鄉土材用和景觀樹種，屬殼斗科錐屬常綠闊葉喬木，生長于海拔30~1300 m緩坡和山地常綠闊葉林中，分布于華南、華中、華東和西南地區，越南、老撾、柬埔寨、緬甸、印度等國家也有分布；廣州市僅見于從化、花都兩個郊區市的山地林中[1-2]。由于城市區域天然林所剩無幾，野生紅錐已不多見，但人們開始重視包括紅錐在內的鄉土闊葉樹種在城市景觀林建設、熱帶亞熱帶次生林經營中的應用[3-4]。

已見許多關于樹種胸高直徑（胸徑）分布的研究[5-11]，但大多局限于韋伯分布（又稱威布爾分布）、正態分布等少數幾種統計分布，而對于冠幅、基徑（即地徑）、樹高等多個個體大小（Body size）指標及其綜合指標，同時運用多種統計分布模型來擬合的研究，鮮有報導。最近，在生態和進化研究的一些領域，研究人員開始采用被稱為“模型選擇”途徑，而非傳統的零假設檢驗途徑[12]。殷祚云將這種模型選擇途徑運用于植物群落中物種多度分布（Species abundance distribution, SAD）的研究中，提出了一個“序列模型集合”以同時模擬觀察數據，從而找到了最佳模型或普適模型——對數柯西分布，并藉此闡明了不同群落不同演替階段物種多度分布的格局與動態[13-17]。

本研究通過精心設計和詳細調查，測得幼齡期紅錐的多個個體大小指標（或生長指標、生長量指標）的大樣本數據，用以探討這些指標的觀察分布與多種理論分布之間的相互關聯，旨在尋找適合這些指標各自的最佳模型及符合所有指標的普適模型，從而闡明其統計分布規律，亦為相關研究提供參考。

1 方法

1.1 研究地概況與調查方法

廣州市地處廣東省中部的南亞熱帶季風海洋性氣候區，夏熱冬暖，雨量充沛，雨熱同季，地帶性植被為季風常綠闊葉林。設在廣東省龍眼洞林場筲箕窩的試驗地（北緯23°13′48″ ~ 23°13′56″、東經113°23′52″ ~ 113°24′04″）位于廣州市東北郊，屬丘陵地區，土壤為山地赤紅壤，原為馬占相思采伐跡地。2010年5月林場采用20~30 cm高、一年生的紅錐容器苗進行再造林，株行距為2.5 m×3 m。2012年5月，在整個試驗區內有代表性地設置了24個10 m×10 m固定樣方，所處海拔101~181 m（平均136.3 m），坡度25°~37°（平均31.5°），坡向從西北、東北、西南、南面、東南到東面；逐株調查每個樣方內的存活個體，所登記個體大小指標包括樹高、冠幅、胸徑和基徑（即地徑）。

1.2 統計分布模型

選擇12個具有不同函數形式的主要連續型分布[14,18-21]（SPSS Inc., 2004），這些理論分布多少有些貌似紅錐個體大小指標的觀察分布。其中，瑞利、指數分布為單參數分布，另外10個均為雙參數分布。

1.2.1 正態分布（常態分布, Normal distribution） 概率密度函數（或稱分布密度、密度函數，Probability density function, PDF）：

累積分布函數（或稱分布函數，Cumulative distribution function, CDF）：

其中，均值μ為位置參數（location parameter），標準差σ為尺度參數（又稱比例參數，scale parameter）。

1.2.2 瑞利分布（Rayleigh distribution）

概率密度函數：

累積分布函數：

F(x;λ)=1?e?(x/λ)2。

其中，λ是尺度參數。

瑞利分布是下述韋伯分布的特例：Rayleigh(x; λ)=Weibull(x; λ, 2)。

1.2.3 指數分布（也叫負指數分布，Exponential distribution）

概率密度函數：

累積分布函數：

F(x;λ)=1?e?λx。

其中，λ為尺度參數。

指數分布既屬于韋伯分布族，也屬于伽瑪分布族，有：

Exp(x; λ)=Weibull(x; 1/λ, 1)=Γ(x; 1, λ)。

1.2.4 伽瑪分布（亦作伽馬分布，Gamma distribution）

概率密度函數：

累積分布函數：

其中，k是形狀參數（Shape parameter），λ是尺度參數。

伽瑪分布適用于各種形式的分布，具有理論意義，其中Γ(1, λ)為指數分布，Γ(n/2,1/2)為自由度為n的卡方分布。

1.2.5 對數正態分布（Lognormal distribution）

概率密度函數：

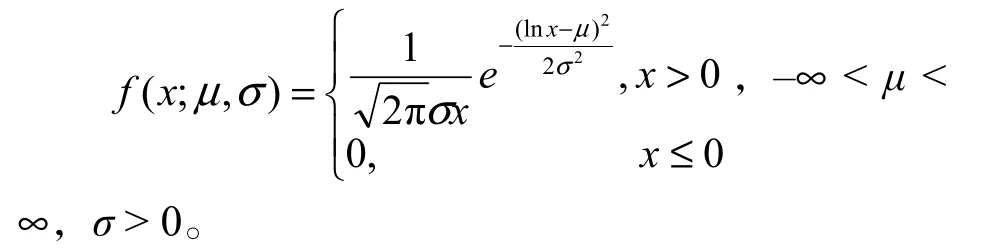
累積分布函數：

其中，μ為位置參數，σ為尺度參數。

1.2.6 韋伯分布（威布爾分布,Weibull distribution） 概率密度函數：

累積分布函數：

F(x;λ,k)=1?e?(x/λ)k。

其中，λ是尺度參數，k是形狀參數。韋伯分布的累積分布函數是擴展的指數分布累積分布函數，且它與很多分布都有關系：當k=1，是指數分布；k=2時，是瑞利分布[18-19]。

1.2.7 柯西分布（哥西分布，Cauchy distribution）

概率密度函數：

累積分布函數：

其中，θ為位置參數，λ為尺度參數。

1.2.8 邏輯斯諦分布（邏輯斯蒂、若吉斯蒂克分布，Logistic distribution）

概率密度函數：

累積分布函數：

其中，μ是均值、位置參數，λ是尺度參數。

1.2.9 極值分布（Extreme value distribution）

概率密度函數：

累積分布函數：

其中，θ為位置參數，λ為尺度參數。

1.2.10 拉普拉斯分布（Laplace distribution）

也叫雙指數分布；對應于正態分布為第二型拉普拉斯分布，又稱第一型拉普拉斯分布。

概率密度函數：

累積分布函數：

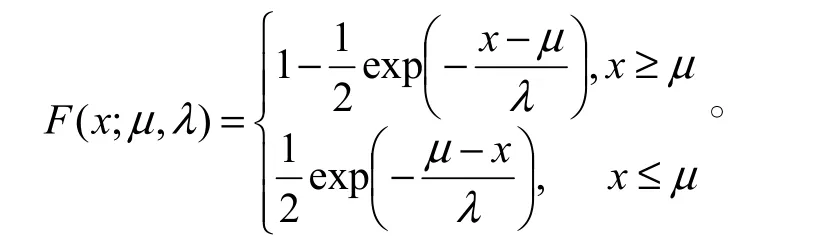
其中，μ是均值、位置參數，λ是尺度參數。

1.2.11 反高斯分布（或逆高斯分布，Inverse Gaussian distribution）

概率密度函數：

累積分布函數：

其中，μ是均值、位置參數，λ是尺度參數(SPSS Inc., 2004)。

1.2.12 對數柯西分布（LogCauchy distribution）

概率密度函數：

累積分布函數：

其中，θ為位置參數，λ為尺度參數。

1.3 數據分析

分布參數估計采用最大或然法[14,16,18]，也可得到或然函數值，用于計算模型對數據的擬合優度（或稱適合度，Goodness of fit）標準：

AIC = ?lnL + K；

CAIC = ?2lnL + K(lnS + 1)。

式中，AIC＝Akaike信息標準（Akaike information criterion）；CAIC＝一致性Akaike信息標準（Consistent AIC）；lnL＝或然函數值的對數；K＝估計參數的個數；S＝樣本大小，即觀測值個數。AIC和CAIC越小，模型越好[22-25]。

同時，還采用各分布的累積分布函數對各指標的累積頻數數據進行基于最小二乘法的非線性回歸分析，求得決定系數R2，用于模型評優；R2值越大，模型越好[16,21,26-27]。

此外，還要進行分布模型是否符合觀察分布的統計顯著性檢驗，由于紅錐個體大小指標均為連續性數據，宜運用柯爾莫哥洛夫－斯米爾諾夫檢驗（Kolmogorov–Smirnov test, KS test）。KS檢驗統計量定義為：當隨機變量取一系列值（通常呈等差數列）時，所得累積觀察分布和累積期望分布之差的絕對值中最大的一個[19,28-29]。根據樣本大小與組數的關系，確定組數；再根據極差決定組距，最后對各個指標數據進行歸組[30]，以用于KS檢驗。設3個置信水平即α＝0.01、0.05和0.20，分別表示較符合、符合和極符合；KS統計量大于α＝0.01水平臨界值時為不符合[28]。

數據處理與分析采用幾種常用軟件完成[31-34]，包括：SPSS 13.0 (SPSS Inc., 2004)、Microsoft Office Excel 2007 (Microsoft Corporation, 2006)、Microcal Origin 5.0 (Microcal Software, Inc., 1997)、OriginPro 7.5 (OriginLab Corporation, 2003)及Mathematica 4 (Wolfram Research, Inc., 1999)。

2 結果

在廣東省龍眼洞林場筲箕窩試驗地的24個固定樣方內總共記錄了145株紅錐，其中127株可測胸徑；為比較包括胸徑在內的全部指標及其衍生指標的統計分布，本研究以這127株紅錐為研究對象（表1）。關于峰度和偏度，4個一維（次）指標即冠幅、胸徑、基徑和樹高以及2個二維指標冠層面積、基部面積很近似于0，可認為它們的總體分布為正態分布；胸高面積、體積明顯大于0，顯然是偏離正態的；三維指標中，冠層體積、基部體積比胸高體積更趨近于0，故也較為接近正態。這與后面的統計檢驗結果（表2—11）是一致的。

表1 廣州市二年生紅錐10種個體大小指標觀測值的描述性統計 Table 1 Descriptive statistics of 10 observed body size indicators of 2-year Castanopsis hystrix in Guangzhou, South China

從10個指標來看，AIC和CAIC的變化趨勢幾乎是一樣的（表2—11），且由于這2個擬合優度標準與KS統計量一樣，都是越小越好[22,24]，而決定系數R2則是越大越好[16,26]，因而本文提出一個新的綜合統計量CAIC×KS/R2，用以綜合判定不同分布模型對各生長指標觀察分布的擬合優度。

對于冠幅的頻數分布（表2），以越小越好的綜合統計量CAIC×KS/R2為標準，分布適合度大小次序為：伽瑪>對數正態>反高斯>正態>極值>邏輯斯諦>韋伯>拉普拉斯>對數柯西>柯西>瑞利>指數，前3名的綜合擬合優度差異不大，分別是1.79、1.84、1.93；后3名差異很大。KS檢驗表明，僅瑞利分布、指數分布不符合觀察，柯西分布在0.05置信水平顯著符合，其他分布均在0.20水平極顯著符合。

表2 十二種統計分布模型對廣州市二年生紅錐冠幅頻數分布的 擬合優度比較 Table 2 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of canopy diameter (CD) of 2-year Castanopsis hystrix in Guangzhou, South China

表3 十二種統計分布模型對廣州市二年生紅錐胸徑頻數分布的 擬合優度比較 Table 3 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of diameter at breast height (BD) of 2-year Castanopsis hystrix in Guangzhou, South China

KS檢驗表明，反高斯分布和指數分布不適合胸徑數據，對數柯西分布和對數正態分布在0.05置信水平符合，其余6個指標都是極為符合（表3）。以綜合統計量為標準進行比較，適合胸徑頻數分布的程度，從大到小依次是：邏輯斯諦>韋伯>極值>正態>瑞利>柯西>拉普拉斯>伽瑪>對數正態>對數柯西>反高斯>指數。前3位差別不大，其后的正態、瑞利、柯西、拉普拉斯和伽瑪分布差不多，再后的對數正態和對數柯西分布也很接近。

瑞利分布和指數分布不適合描述基徑的觀察分布，其他指標則都極顯著符合（表4）。各分布模型對基徑觀察分布的擬合優度排序為：對數柯西>伽瑪>邏輯斯諦>正態>韋伯>極值>對數正態>反高斯>拉普拉斯>柯西>瑞利>指數。位于第1位的對數柯西分布大大優于其后的3個分布，再后的韋伯、極值、對數正態、反高斯分布較為接近，拉普拉斯與柯西分布相差不大，而最后2個分布的綜合統計量特別的高，因而不適合基徑數據。

表4 十二種統計分布模型對廣州市二年生紅錐基徑頻數分布的 擬合優度比較 Table 4 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of ground diameter (GD) of 2-year Castanopsis hystrix in Guangzhou, South China

根據KS檢驗，樹高分布與冠幅、基徑分布一樣，顯然也不適合由指數和瑞利分布來描述，但極顯著地服從其他8種分布模型（表5）。12個理論分布對樹高數據的擬合優度排名如下：對數柯西>伽瑪>拉普拉斯>邏輯斯諦>對數正態>反高斯>正態>極值>韋伯>柯西>指數>瑞利。樹高與基徑一樣，最為適合的也是柯西分布，但與緊隨其后的伽瑪、拉普拉斯、邏輯斯諦分布，在綜合統計量上的差異不是很大；從對數正態到柯西分布的6個分布較為接近；而位居最后的指數、瑞利分布，其綜合統計量比其他分布的大1~2個數量級。

對于冠層面積，僅指數分布不符合其觀察分布，正態和柯西分布在0.05置信水平符合，其他分布都是極符合（表6）。擬合優度順序為：反高斯>對數正態>極值>伽瑪>邏輯斯諦>瑞利>韋伯>對數柯西>拉普拉斯>正態>柯西>指數。仍就綜合統計量而言，最適合的反高斯分布與緊接著的對數正態、極值分布相近，而后的伽瑪、邏輯斯諦、瑞利和韋伯分布差不多，對數柯西、拉普拉斯、正態和柯西分布較接近，排最后的指數分布則奇高。

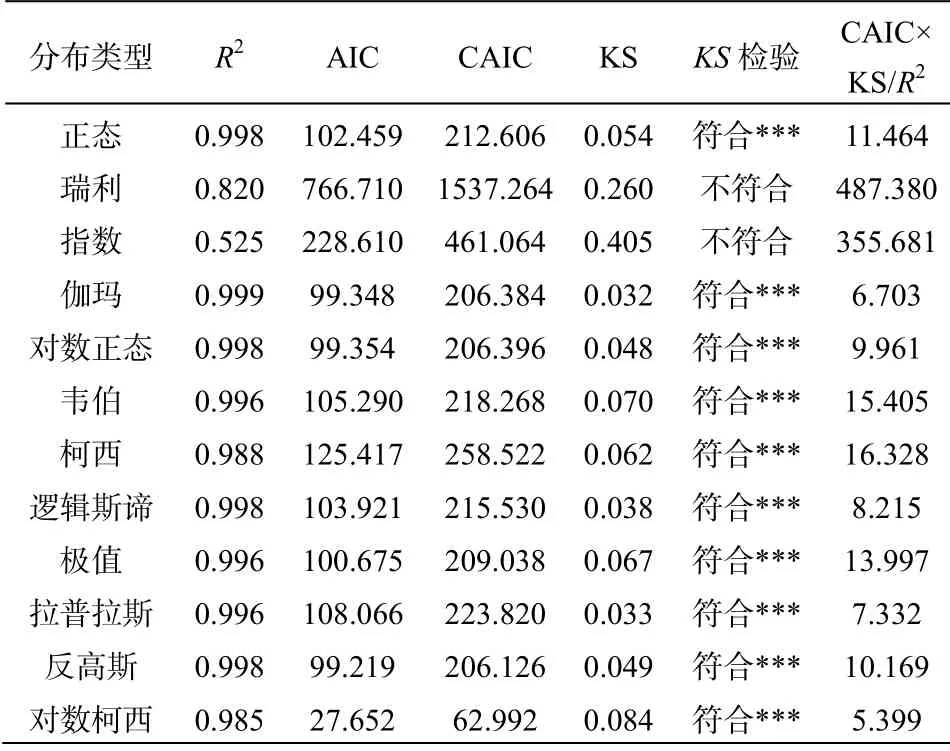
表5 十二種統計分布模型對廣州市二年生紅錐樹高頻數分布的 擬合優度比較 Table 5 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of tree height (HT) of 2-year Castanopsis hystrix in Guangzhou, South China

表6 十二種統計分布模型對廣州市二年生紅錐冠層面積頻數分布的 擬合優度比較 Table 6 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of canopy area (CA) of 2-year Castanopsis hystrix in Guangzhou, South China

令人驚奇的是，單參數的指數分布竟然成為模擬胸高面積頻數分布的最佳模型，排在其后的韋伯和伽瑪分布，其綜合統計量與指數分布的相差較小；再后的極值、邏輯斯諦、拉普拉斯分布相距不大；對數正態、柯西和對數柯西分布較為接近（表7）。擬合優度順序為：指數>韋伯>伽瑪>極值>邏輯斯諦>拉普拉斯>對數正態>柯西>對數柯西>正態>反高斯>瑞利。由KS檢驗可知，正態、反高斯、瑞利分布不適合模擬實測數據，對數正態分布在0.01水平較適合，柯西和對數柯西分布在0.05水平適合，其他均在0.20水平極適合。

對基部面積的擬合優度次序為：伽瑪>極值>對數柯西>邏輯斯諦>韋伯>對數正態>瑞利>反高斯>拉普拉斯>正態>柯西>指數（表8）。排在第二位的極值分布綜合統計量與最佳模型伽瑪分布的很相近，排在第三的對數柯西分布則稍大些，而后的邏輯斯諦、韋伯、對數正態和瑞利較接近，再后的反高斯、拉普拉斯和正態分布相仿，柯西分布的綜合統計量則很大，指數分布最大，高出其他分布1個數量級。KS檢驗也表明，擬合優度排末尾的指數分布不符合基部面積的觀察分布；柯西分布在0.05置信水平符合；其他分布均在0.20水平極顯著地適合觀察。

表7 十二種統計分布模型對廣州市二年生紅錐胸高面積頻數分布的 擬合優度比較 Table 7 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of area at breast height (BA) of 2-year Castanopsis hystrix in Guangzhou, South China

表8 十二種統計分布模型對廣州市二年生紅錐基部面積頻數分布的 擬合優度比較 Table 8 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of ground area (GA) of 2-year Castanopsis hystrix in Guangzhou, South China

據KS檢驗可得，冠層體積分布除了不服從指數分布、較顯著地服從瑞利和正態分布之外，均極顯著地服從其他9種統計分布，擬合優度排位為：對數正態>反高斯>伽瑪>極值>對數柯西>韋伯>拉普拉斯>邏輯斯諦>柯西>瑞利>正態>指數（表9）。其最佳模型對數正態分布的綜合統計量明顯低于位居第二的反高斯分布；伽瑪與極值較接近；對數柯西、韋伯、拉普拉斯和邏輯斯諦相近；瑞利與正態差不多；指數分布則明顯最大。

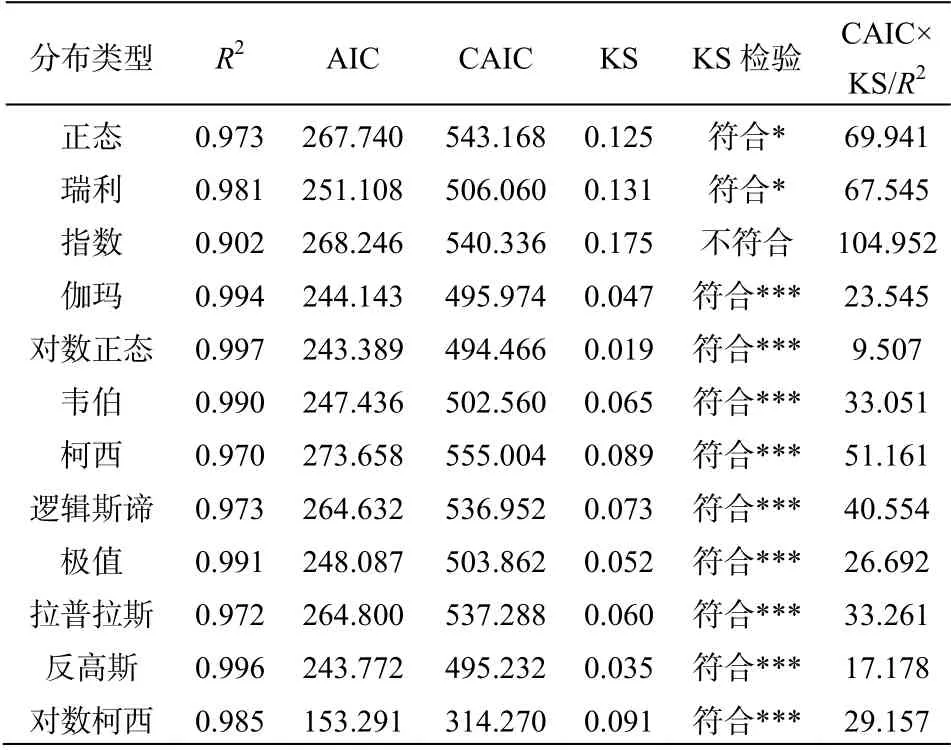
表9 十二種統計分布模型對廣州市二年生紅錐冠層體積頻數分布的 擬合優度比較 Table 9 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of canopy volume (CV) of 2-year Castanopsis hystrix in Guangzhou, South China

表10 十二種統計分布模型對廣州市二年生紅錐胸高體積頻數分布的擬合優度比較 Table 10 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of volume at breast height (BV) of 2-year Castanopsis hystrix in Guangzhou, South China

對于胸高體積分布的擬合優度，韋伯>伽瑪>指數>對數正態>對數柯西>拉普拉斯>邏輯斯諦>極值>柯西>正態>反高斯>瑞利（表10）。綜合統計量韋伯比伽瑪稍低，比排第三位的指數分布低2倍以上；但與胸高面積類似，指數分布能如此適合胸高體積數據，較為少見；對數正態、對數柯西和拉普拉斯差不多；邏輯斯諦、極值和柯西較相近；從正態、反高斯到瑞利分布，綜合統計量都很大，且越來越明顯增大。KS檢驗也表明后面3個分布不適合觀察分布；而對數柯西、極值和柯西分布在0.05水平上符合觀察；其余分布都在0.20水平極符合。

至于基部體積，擬合優度排序為：對數柯西>伽瑪>對數正態>韋伯>反高斯>極值>邏輯斯諦>拉普拉斯>正態>柯西>瑞利>指數（表11）。前3名的綜合統計量較接近；緊接著的4個分布也相近；再后的邏輯斯諦、拉普拉斯、正態、柯西分布，綜合統計量達到3位數；最末一位指數分布的綜合統計量明顯高于倒數第二位的瑞利分布。從KS檢驗可知，基部體積僅不服從指數分布，服從其他分布——在0.01水平較顯著服從瑞利分布，在0.05水平顯著服從正態、柯西和拉普拉斯分布，而在0.20水平極顯著服從另外7個分布。

表11 十二種統計分布模型對廣州市二年生紅錐基部體積頻數分布的擬合優度比較 Table 11 Comparisons of the goodness-of-fits of 12 statistical distribution models to the frequency distribution of ground volume (GV) of 2-year Castanopsis hystrix in Guangzhou, South China

綜合上述結果顯示（表2—11），一般說來，同樣的分布模型即正態分布或柯西分布，對數尺度比之線性尺度，更適合觀察分布。以綜合統計量CAIC×KS/R2為評判標準，這兩種類型的分布對10個指標的擬合優度順序列舉如下：

冠幅：對數正態>正態，對數柯西>柯西；

胸徑：正態>對數正態，柯西>對數柯西；

基徑：正態>對數正態，對數柯西>柯西；

樹高：對數正態>正態，對數柯西>柯西；

冠層面積：對數正態>正態，對數柯西>柯西；

胸高面積：對數正態>正態，柯西>對數柯西；

基部面積：對數正態>正態，對數柯西>柯西；

冠層體積：對數正態>正態，對數柯西>柯西；

胸高體積：對數正態>正態，對數柯西>柯西；

基部體積：對數正態>正態，對數柯西>柯西。也就是說，在10個指標20種情形中僅有胸徑、基徑和胸高面積3個指標4種情形是例外，其他16種情形都是對數尺度比線性尺度為優。這顯然不是偶然的。

前面的分析還表明，伽瑪、韋伯、邏輯斯諦3個分布均在0.20置信水平極顯著地適合描述紅錐的全部10個個體大小指標，成為表現最好的3個普適模型；極值和拉普拉斯分布各僅一個指標在0.05水平符合，其他在0.20水平符合，表現也不錯；對數柯西、對數正態分布及柯西分布也可以；而常用的正態分布有胸高面積和胸高體積2個指標不適合，瑞利、指數和反高斯分布分別有5個、8個和3個指標不符合。

現在比較伽瑪、韋伯、邏輯斯諦3個普適分布（表2—11）。對綜合統計量CAIC×KS/R2進行排名后可知，在全部10個指標中，從排名領先的指標比例來看，伽瑪分布與韋伯分布為7:3，伽瑪與邏輯斯諦是9:1，可見伽瑪分布優于韋伯分布、明顯優于邏輯斯諦分布；而已有研究中常用的韋伯分布與不常用的邏輯斯諦分布領先指標比例為4:6，韋伯分布還不如邏輯斯諦分布。綜上所述，伽瑪分布是最佳的普適模型，因而可用來比較所有個體大小指標內在的統計分布格局差異（圖1）。

適合模擬全部10個指標統計分布的伽瑪分布曲線清楚地顯示出同一維度不同指標、同類指標不同維度之間偏態和峰態的差異（圖1）。4個一維（次）指標分布曲線，除胸徑略微左偏（正偏）外，幾乎都呈左右對稱的鐘形曲線，這與表1的描述統計（其中胸徑的偏度最大）是一致的。只有胸高面積、體積的分布曲線變成凹形（或稱倒J形、雙曲線形），其他指標都呈單峰形，這是與胸高面積、體積頻數分布的偏度遠大于0、且在10個指標中最大有關（表1），也就是它們嚴重違背正態分布的原因（表7、10）。2個二維指標冠層面積和基部面積的分布曲線接近鐘形，另一個二維指標胸高面積呈凹形，這也與前面描述統計的結果一致（表1）；3個三維（次）指標即冠層、胸高、基部體積，也表現類似格局。

各指標伽瑪分布曲線的變化規律與分布參數的變化趨勢是一致的。從長度（直徑和高度）、面積到體積，即個體大小指標從一、二到三維（次），曲線高度越來越矮，越來越左偏，以至變為凹形（胸高面積、體積），而且越來越凹——胸高體積比胸高面積更向左凹陷。這與所擬合伽瑪分布參數的變化規律相對應：從直徑、面積到體積，無論冠層、胸高還是基部，形狀參數k、尺度參數λ兩個參數都是遞減的（表12）。

圖1 擬合廣州市二年生紅錐10種個體大小指標觀察分布的 伽瑪分布曲線比較 Fig.1 Comparisons of the gamma distribution curves fitting to the observed distributions of 10 body size indicators of 2-year Castanopsis hystrix in Guangzhou, South China

表12 模擬廣州市二年生紅錐10種個體大小指標觀察分布的伽瑪分布之參數最大或然估計 Table 12 Maximum likelihood estimation of the gamma distribution parameters modeling the observed distributions of 10 body size indicators of 2-year Castanopsis hystrix in Guangzhou, South China

3 討論

幼齡期紅錐的全部個體大小指標都有各自最適合的分布模型（且大多不適合常用分布），同時也存在共同遵從的分布模型，這是個性與共性的完美結合。冠幅、胸徑、基徑、樹高、冠層面積、胸高面積、基部面積、冠層體積、胸高體積和基部體積等10個指標的最佳模型分別是伽瑪、邏輯斯諦、對數柯西、對數柯西、反高斯、指數、伽瑪、對數正態、韋伯和對數柯西分布，其中對數柯西分布占了3個指標，伽瑪分布2個，其余均為1個。可以看出，與最佳的普適模型伽瑪分布相比，對數柯西分布表現也較好——在KS檢驗中僅胸徑、胸高面積、胸高體積3個指標為顯著適合，其他7個指標均為極顯著適合，這類似于生物群落中物種多度分布（SAD）：分別在3個模型組成的集合和7個模型組成的集合中，都是對數柯西分布表現最佳[14,16-17]。值得注意的是，全部10個指標所服從的最佳統計分布模型都不是通常所假設的正態分布，并且只有胸高體積一個指標的觀察分布服從常用的韋伯分布。

不同維度指標的統計分布具有不同的表現。10個指標擬合伽瑪分布曲線顯示，同一維度不同指標、同類指標不同維度之間的偏態和峰態存在明顯差異。個體大小指標從長度（直徑和高度）、面積到體積，即從一、二到三維（次），曲線高度越來越矮，越來越趨于正偏（即曲線高峰向左偏離均值）[35]，以至變為凹形，而且越來越向左凹陷。另一方面，分布模型適合度與指標尺度有關。總的說來，對數尺度的柯西分布、正態分布（即對數柯西分布、對數正態分布）分別比線性尺度的相同分布擬合優度更大。因此，在進行基于正態分布假設的各種統計檢驗、推斷時應格外謹慎。在某些情形下，先對觀察數據——特別是較高維度的數據——進行對數等非線性尺度的轉換，再進行統計分析，將會得到更有說服力的結論。在當今生態學較為熱門的碳匯研究中，生物量或固碳量與三維指標，如木材蓄積量或本文提及的冠層、胸高和基部體積，通常呈線性正相關，因而在進行統計分析時，應考慮其中可能存在的非正態性或非對稱性。此外，本研究中的面積指標與葉面積指數、地被物蓋度和郁閉度同屬二維指標，也應呈線性正相關，因此，這里所揭示的二維面積指標統計分布規律亦可為后面這些常用指標的調查研究提供借鑒。

本研究結果可為林木遺傳育種、栽培和種群生態學等領域研究提供參考。僅僅考察某一樹種不同種源、家系、無性系或單株之間某個個體大小指標平均值的差異顯著性，是不全面的，未能充分揭示實測數據中所蘊含的大量統計信息，而應從多方位、多角度考察其間可能存在的差異，即：就各個指標，弄清它們之間其他樣本統計量（如偏態、峰態和變異系數）及該指標所屬總體分布的參數大小、曲線形狀等方面的異同所在。值得一提的是，對特定物種的天然或人工種群的長期跟蹤（尤其是定期定位）研究，有利于揭示其內在的統計分布動態規律，因而將具有更加重大的理論和實踐意義。

提出一個綜合評價擬合優度的統計量CAIC×KS/R2。這個統計量綜合考慮了3個不同角度、多個不同方面：CAIC——考慮了最大或然函數值、參數個數和樣本大小等3個方面[24-25]，CAIC越小越好；KS統計量——對應于隨機變量的完全取值序列（通常是等差數列），累積觀察分布與累積期望分布差異絕對值中的最大值[19,28-29]，也是越小越好；R2——采用最小二乘法進行非線性回歸時所得最小殘差（或剩余）平方和的補，考慮了隨機變量全序列取值時累積觀察分布與累積期望分布差異的平方和，殘差越小，R2越大，模型越好[14,26]。單一標準評判模型優劣，容易得出片面乃至不實之結論。

4 結論

紅錐是南亞熱帶地區重要的材用和景觀樹種，也是廣東省珍貴的鄉土常綠闊葉樹種。現有研究很少報導運用多個統計分布模型，同時對某一樹種多個個體大小指標的頻數分布進行擬合和比較。本研究精心設計了廣州城市景觀林固定樣地，仔細調查了其中二年生紅錐的冠幅、胸徑、基徑和樹高4個指標。選用12個具有不同函數形式的主要連續型分布，組成一個相對完整的模型集合，運用最大或然法和最小二乘法，同時模擬上述4個長度指標及其衍生的3個面積指標和3個體積指標。研究表明：

(1)10個指標都有各自最適合的分布模型，也共同遵從幾個分布模型，其中以伽瑪分布最佳，其次是邏輯斯諦分布和韋伯分布；

(2)分布曲線形狀因指標的維度而異，從一維直徑和高度、二維面積到三維體積，曲線變得越來越低矮、趨于正偏，甚至從單峰形變成凹形；

(3)期望概率分布對觀察頻數分布的擬合優度與指標的尺度有關，通常是對數尺度優于線性尺度，例如：對數柯西分布比柯西分布更適合模擬10個指標中除胸徑和胸高面積之外的8個指標；

(4)一個整合一致性Akaike信息標準CAIC、Kolmogorov-Smirnov檢驗統計量KS和回歸決定系數R2的統計量CAIC×KS/R2，可作為擬合優度的綜合評價標準。

本研究可望為林木栽培育種和種群生態學等領域的研究提供借鑒。應從多方位、多角度地對某一樹種不同種群各生長指標的頻數分布進行比較，即針對每個指標，闡明這些種群之間除均值外的其他樣本統計量（包括偏態、峰態和變異系數）及其所屬總體分布的參數大小、曲線形狀等方面的異同。而對特定物種的天然或人工種群的長期跟蹤研究，有利于揭示其內在的統計分布動態規律，更是一個值得進一步研究的有趣課題。

致謝：本研究在野外調查和資料收集中得到了廣東省林業科學研究院蔡漢興、謝振鳳、汪鵬和蔡靜如，廣東省龍眼洞林場朱細儉、李宇雪的大力支持，謹此表示衷心感謝！

[1] 葉華谷, 彭少麟. 廣東植物多樣性編目[M]. 廣州: 廣東世界圖書出版公司, 2006.

[2] 邢福武, 曾慶文, 謝左章. 廣州野生植物[M]. 貴州: 百通集團貴州科技出版社, 2007.

[3] 曾令海, 殷祚云. 熱帶次生林經營[M]. 廣州: 廣東省出版集團廣東科技出版社, 2013.

[4] 朱細儉, 黃少鋒, 張志鴻. 紅錐混交林生長情況調查分析[J]. 廣東林業科技, 2003(4): 46-48.

[5] 董文宇, 邢志遠, 惠淑榮, 等. 利用Weibull分布描述日本落葉松的直徑結構[J]. 沈陽農業大學學報, 2006(2): 225-228.

[6] 黃家榮, 孟憲宇, 關毓秀. 馬尾松人工林直徑分布神經網絡模型研究[J]. 北京林業大學學報, 2006(1): 28-31.

[7] 惠淑榮, 呂永震. Weibull分布函數在林分直徑結構預測模型中的應用研究[J]. 北華大學學報：自然科學版, 2003(2): 101-104.

[8] 孟京輝, 陸元昌, 劉剛, 等 海南島熱帶天然林直徑分布模型研究[J]. 華中農業大學學報, 2010(2): 227-230.

[9] 寧小斌, 李永亮, 劉曉農. 基于Weibull分布的林分結構可視化模擬技術研究[J]. 中南林業調查規劃, 2012,02:13-17.

[10] 王秀云, 黃建松, 程光明, 等. 用Weibull分布擬合刺槐林分直徑結構的研究[J]. 林業勘察設計, 2004(2):1-3.

[11] 閆東鋒, 侯金芳, 張忠義, 等. 寶天曼自然保護區天然次生林林分直徑分布規律研究[J]. 河南科學, 2006(3):364-367.

[12] JOHNSON J B, OMLAND K S. Model selection in ecology and evolution[J]. Trends Ecological Evolution, 2004, 19 (2), 101-108.

[13] YIN Z Y, GUO Q, REN H, et al. Seasonal changes in spatial patterns of two annual plants in the Chihuahuan Desert, USA[J]. Plant Ecology, 2005, 178(2): 189-199.

[14] YIN Z Y, PENG S L, REN H, et al. LogCauchy, log-sech and lognormal distributions of species abundances in forest communities[J]. Ecological Modelling, 2005, 184(2/4): 329-340.

[15] YIN Z Y, REN H, ZHANG Q M,et al. Species abundance in a forest community in South China: a case of Poisson lognormal distribution[J]. Journal of Integrative Plant Biology, 2005, 47(7): 801-810.

[16] 殷祚云. Modeling on Species Abundance and Distribution Patterns in Plant Communities[D]. 北京:,中國科學院研究生院, 廣州: 華南植物園, 2005.

[17] 殷祚云, 任海, 彭少麟, 等. 華南退化草坡自然恢復中物種多度分布的動態與模擬[J]. 生態環境學報, 2009, 18(1): 222-228.

[18] 數學手冊編寫組. 數學手冊[M]. 北京: 人民教育出版社,1979.

[19] 方開泰, 許建倫. 統計分布[M]. 北京: 科學出版社, 1987.

[20] 殷祚云, 廖文波. 南亞熱帶森林群落種－多度的對數正態分布模型研究[J]. 廣西植物, 1999, 19(3): 221-224.

[21] 殷祚云. Logistic曲線擬合方法研究[J]. 數理統計與管理, 2002, 21(1): 41-46.

[22] AKAIKE H. Information theory and an extension of maximum likelihood principle [C] // PETROV B N, CSAKI F. Proceedings of the Second International Symposium of Information Theory. Budapest: Akademiai Kiado, 1973, pp 267-281.

[23] WANG W, FAMOYE F. Modeling household fertility decisions with generalized Poisson regression [J]. Journal of Population Economics, 1997, 10:273-283.

[24] GURMU S,TRIVEDI P K. Excess zeros in count models for recreation trips [J]. Journal of Business and Economic Statistics, 1996, 14: 469-477.

[25] MELKERSSON M,ROOTH D O. Modeling female fertility using inflated count data models [J]. Journal of Population Economics, 2000, 13:189-203.

[26] QUINN G P, KEOUGH M J. Experimental Design and Data Analysis for Biologists [J]. Cambridge:Cambridge University Press, 2002.

[27] 殷祚云, 任海, 曾令海, 等. 三參數增長模型擬合: 以季風常綠闊葉林中兩個優勢喬木種群為例[J]. 生物數學學報, 2006, 21(3): 428-434.

[28] GLOVER T J, MITCHELL K J. An Introduction to Biostatistics [M]. New York: McGraw-Hill, 2001.

[29] DETSIS V, DIAMANTOPOULOS J, KOSMAS C. Collembolan as-semblages in Lesvos Greece:effects of differences in vegetation and precipitation [J]. Acta Oecologica, 2000, 21(2):149-159.

[30] 馬育華. 田間試驗和統計方法[M]. 北京: 農業出版社, 1979.

[31] 宇傳華, 顏杰. Excel與數據分析[M]. 北京: 電子工業出版社, 2002.

[32] 郝紅偉, 施光凱. Origin 6.0實例教程[M]. 北京: 中國電力出版社, 2000.

[33] 盧紋岱, 朱一力, 沙捷, 等. SPSS for Windows從入門到精通[M]. 北京: 電子工業出版社, 1997.

[34] 楊鈺, 何旭洪, 趙昊彤. Mathematica應用指南[M]. 北京: 人民郵電出版社, 1999.

[35] 杜榮騫. 生物統計學[M]. 北京: 高等教育出版社, 1985.