三維標號的實時矢量生成技術

圣長軍，王家潤，王玉玫

(華北計算技術研究所，北京100083)

0 引言

由于三維戰場態勢提供了豐富的空間信息和逼真的戰場環境，因此相比于傳統的二維戰場態勢，它必將在現代信息化戰爭中占據更加重要的作用。作為三維戰場態勢系統的重要組成部分，三維標號的生成是國內外研究的熱點。目前國內還沒有針對三維標號的顯示制定統一的圖形標準，這使得三維標號的制作方法多種多樣，現有的方法都是對不同類型的標號使用不同的生成技術。例如點標號的制作一般采用Billboard(公告板)技術，文獻［1］中的點標號就是利用公告板技術制作而成，它采用改進的浮雕算法處理軍標圖像，增強了公告板顯示的立體感。對于線面標號的生成，主要采用三類方法:基于RTT(render to texture)技術的繪制方法、基于矢量數據的繪制方法和基于模板陰影體技術的繪制方法。文獻［2］中介紹了這三類方法的實現過程，并敘述了它們的優缺點，本文不展開敘述。

鑒于三維標號生成的這種復雜局面，本文提出一種完全基于矢量數據的繪制方法。該方法不但可以用于線面標號的生成，而且對點標號的生成同樣適用;該方法統一了不同類型標號的生成過程，同時避免了Billboard中立體感缺失和RTT技術下紋理走樣的問題。

1 三維標號生成方法

本文的三維標號生成方法是以現有的二維標號算法為基礎，通過對其圖元結果進行改造，獲得相應的三維繪制基礎圖元，然后使用OpenSceneGraph［3］(OSG)構造出三維標號，最后再進行一些特效處理，圖1所示為二、三維標號的繪制流程。

1.1 二維標號繪制簡介

眾所周知，操作系統提供的圖形設備接口 (如windows下的GDI+)只能用于繪制諸如文字、點、線段、多邊形、橢圓、圓弧、Bezier曲線等基礎圖元。因此，要繪制任意一個二維標號，必須先將它分解成這些基礎圖元，再調用圖形設備接口進行跟蹤繪制。

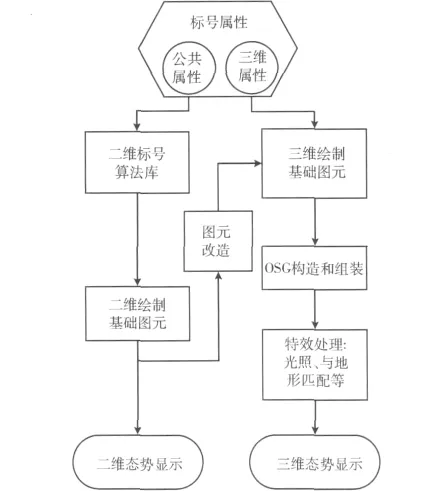
圖1 二、三維標號的繪制流程

參見圖1可知二維標號的繪制過程:首先標號經過二維標號算法庫被分解為基礎圖元，然后在二維圖形系統中進行繪制和顯示。

其中，二維標號算法庫封裝了對所有二維標號的屬性解釋和圖元分解過程，它的意義在于屏蔽了標號形狀的差異，使得圖形設備接口能夠順利繪制出二維標號。由此可見，二維標號算法是整個二維標號生成過程中的核心部分。

圖2以某實際標號為例，說明該標號經過二維標號算法庫處理后分解成二維繪制基礎圖元的結果。由圖可知，為了在二維態勢下顯示該符號，二維圖形系統只需依次繪制4個基礎圖元即可，包括一個圓、一段圓弧和兩條線段。

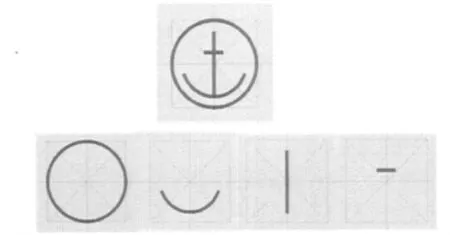
圖2 標號分解成基礎圖元

1.2 三維標號生成設計

三維標號的生成方法采取了與二維標號類似的思路，該方法關鍵在于如何將標號分解成為三維繪制基礎圖元。本文選擇充分利用現有的二維標號算法庫技術，盡管它最終產生的只是二維的圖元數據，但是通過對這些二維圖元數據進行適當改造，可以獲得標號的三維圖元數據。

在將二維圖元數據改造成三維圖元數據的具體實施過程中還需解決如下幾個問題:①如何擴展三維標號特有的屬性數據;②如何將二維繪制基礎圖元的頂點數據從二維平面變換到三維空間;③如何映射二維繪制基礎圖元與三維繪制基礎圖元的類型關系。

針對以上3個問題，提出的解決方案如下:

(1)三維標號的屬性結構設計

三維標號的許多屬性數據是二維標號所沒有的，比如標號的厚度屬性、標號控制點的高度屬性 (二維標號中只有經緯度信息)、標號的光照屬性、點標號面向屏幕顯示屬性以及線面標號與地形匹配屬性等等。為了不影響對原來二維標號算法庫的使用，我們仍然將原有的二維標號屬性獨立保存，將其作為二、三維標號的公共屬性，而將三維標號的特有屬性作為擴展屬性來保存。標號的屬性結構設計層次如圖3所示。

圖3 標號屬性數據的UML設計

(2)圖元數據的三維坐標變換

二維繪制基礎圖元中的頂點數據都是平面的，首先將其一一映射到三維坐標系中的xy平面，如p(x，y)→p'(x，y，0)，這便形成了三維空間中可繪制的頂點形式。然后再通過對映射后的三維頂點數據進行平移、旋轉、縮放等一系列幾何變換，三維標號就能呈現出各種復雜的顯示樣式。

(3)基礎圖元類型的三維映射

最后還需知道，三維圖形繪制系統中的基礎圖元類型相比二維來說要少。OSG中可繪制的圖元類型只包括6種:文字、點、線段、三角形、四邊形和 (凸)多邊形。其他任何復雜的圖形都是通過這幾種基礎類型組合而成。對照二維標號算法庫分解出的基礎圖元可知，除了相同類型的圖元可以一一映射外，像橢圓、圓弧、Bezier曲線等在三維態勢下仍然無法直接繪制，還需要對它們做進一步的分解工作，將它們分解成OSG中可繪制的線段類型。

通過以上 (1)、(2)、(3)三個步驟，最終獲得了標號的三維繪制基礎圖元。以上三個步驟相當于組成了三維標號算法庫，顯然，這種以二維標號算法庫為基礎并對其結果進行分解和坐標轉換的方法很容易實現，工作量也非常小。因此，更多的精力可被集中于后續的三維圖元構造以及標號與地形匹配、光照特效處理等方面。

2 三維標號繪制技術

2.1 三維繪制基礎圖元獲取

由前面的敘述可知，三維繪制基礎圖元是在二維繪制基礎圖元的結果上改造而得。對比二者中的類型可知，需要將二維繪制基礎圖元中的橢圓、圓弧和Bezier曲線分解成連續線段，另外，還需要對面狀標號進行三角剖分。

下面簡要介紹這些分解方法:

(1)橢圓逼近方法

Windows系統下，二維圖形設備接口GDI+提供了函數DrawEllipse，它可以很方便的繪制橢圓。但在三維系統中只能采用連續線段逼近的方式來繪制橢圓，由橢圓參數方程:(其中a為橢圓長半軸，b為橢圓的短半軸，a、b＞0)，可得在其區間取 n等分的頂點依次相連就可以逼近橢圓;當n取值越大，橢圓也就越逼真，但相應的計算代價也越大。

弧形屬于橢圓的一部分，只是θ的取值為弧的起始角度和結束角度之間，θ∈［θs，θe］。圓也屬于特殊的橢圓(此時橢圓方程中a=b)，因此也歸為橢圓類。

(2)貝塞爾曲線構造

同樣的，GDI+中也提供了函數DrawBezier來直接繪制三次貝塞爾曲線，但在三維系統中必須將其分解為連續線段才能繪制，利用Bezier曲線參數方程

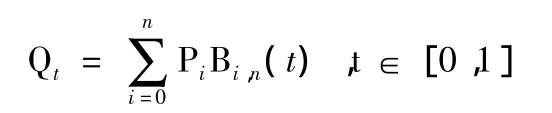
其中pi(i=0，1，…，n)表示Bezier曲線的一系列控制頂點，Bi，n(t)是 Bernstein基函數。對于三次 Bezier曲線，n=4，且點p0和p3為曲線兩端點。

線面標號中實際應用情況是，對于多個控制點Ci(i=0，1，2，…)需要構造出經過所有Ci控制點的光滑曲線，本文使用了分段連續三次 Bezier曲線的構造方法［4］，如圖4所示。

圖4 分段連續三次Bezier曲線控制點構造

步驟如下:①在相鄰的兩個控制點Ci'和Ci″之間構造兩個插入控制點Pi'、Pi″，生成一段Bezier曲線;②插入控制點的構造要滿足使相鄰的兩段Bezier曲線在其過渡點Ci保持C1連續。

(3)面狀標號的三角剖分

對于面狀標號的顯示，GDI+中提供了函數DrawPath，該函數只要結合不同的畫刷就能繪制出單色填充或漸變填充的面狀標號。而三維系統中可繪制的填充形狀只能為凸多邊形，但面狀標號中存在較多的非凸多邊形，必須對其進行三角剖分后方可正確的填充該標號。

對于單色填充的面狀標號，只要直接使用簡單多邊形的三角剖分［5］方法，將面狀標號分解成三角形后給其綁定相同的顏色即可，效果如圖5所示。

對于漸變色填充的面狀標號，則需要采用更為細膩的三角剖分算法。圖6所示，采用了一種滿足顏色漸變需求的規則三角剖分方法，結果表明鉗擊箭頭漸變效果較好。

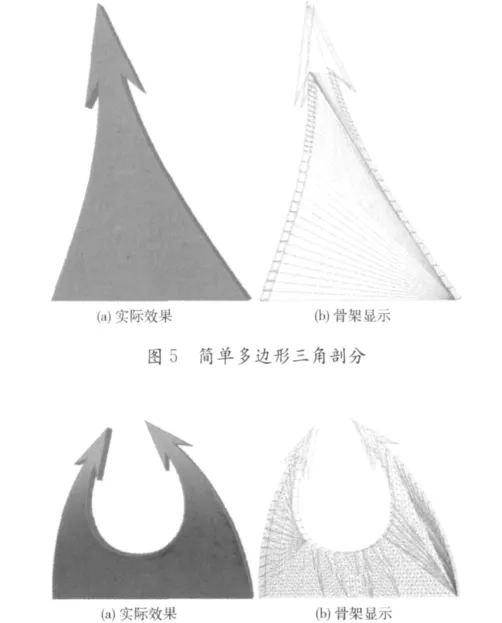
圖6 滿足顏色漸變需求的規則三角部分

2.2 三維繪制基礎圖元構造

標號最終被分解成三維繪制基礎圖元，包括:位圖、文字、線段、三角形、四邊形和 (凸)多邊形。OSG提供了對所有這些圖元進行繪制的方法，其中針對文字還提供了兩種類型:Text和Text3D(平面文字和立體文字)，為了提高繪制效率本文使用平面文字的繪制方式。

由這些基礎圖元數據已經可以繪制平面的三維標號，此時再加入寬度和厚度屬性就能夠構造出三維立體標號。由解析幾何知識可知，二維繪制基礎圖元中的一條線段映射到三維空間中的xy平面后仍然是一條線段。要將這條線段擴展成立體的形狀，需經過如下兩個步驟:①將線段在xy平面上向兩側拉伸出寬度;②將線段在z軸方向上拉伸出厚度。圖7中 (a)為擴展前的點標號，(b)為擴展后的立體效果，(c)為立體標號的骨架顯示效果。

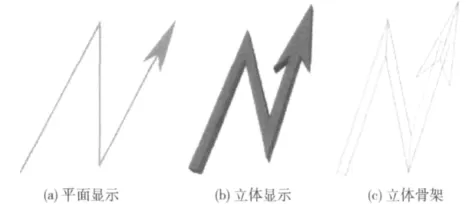
圖7 三維立體標號

步驟①采用平行線算法，如圖8所示，對于連續線段ABCD，先在其右側構造平行線ArBrCrDr，假設標號線寬為w，則AAr垂直于AB，且為B點處的角平分線，且點Cr屬于中間點，其求解方法與Br相同;點Dr屬于端點，其求解方法與Ar相同。同理可在ABCD左側構造出平行線AlBlClDl。

圖8 連續線段平行線算法示意

至于厚度的拉伸，只需在前一步寬度拉伸基礎上將每個頂點的高度增加一定值即可。對平行線每點高度z值增加厚度d后，可得拉伸后的數據同理可得平行線AlBlClDl的厚度拉伸數據

至此，獲得了四組頂點數據，并且由每個頂點數組所表示的線段都是原線段ABCD在三維空間中的平行線。OSG中只要以GL_QUADS繪制模式將這些頂點數據按一定規則連接成四邊形，就生成了線段的立體模式。需要特別注意的是，指定四邊形時需要嚴格確保頂點的繪制順序使得四邊形的法線方向為指向標號的外部，否則將無法正確地顯示光照效果。

2.3 三維標號與地形匹配

點標號與地形匹配方法非常簡單，只要保證點標號定位點的高度值位于地形上方即可。因此，在標繪三維點標號時需要實時的查詢其經緯度所在位置對應的地形高程值。

對于線面標號而言，與地形匹配的方法顯得非常重要，如若線面狀標號不能與地形合理匹配，那么在地形起伏較大的區域顯示時易出現懸浮空中和陷入地下的情況。本文使用較為簡單的解決方法——查詢線面標號每個數據點對應經緯度位置的高程值。根據前面的平行線算法介紹可知，實際需要查詢的高程數據只要包括三維基礎圖元數據對應的那條主線段 (如圖8中的線段ABCD)上的所有頂點即可，立體擴展后各線段相對這條主線段是固定的，其頂點數據可通過平移獲得。以上介紹的這種線面標號與地形匹配的方法，它的實時計算速度基本可以滿足三維態勢下對線面標號的繪制要求，但對于態勢演播這種需要短時間內進行大量標號更新的功能而言，這種方法則延遲較為明顯，這也是本文需要改進的地方。文獻［6］中給出了一種基于GPU的方法解決線面狀標號與地形匹配問題，該方法運算效率較高，可供讀者進一步研究。

3 實驗結果

圖9為戰場態勢二維標繪系統下的標號效果，圖10為相應的三維標號效果。

結果表明，使用本文方法生成的三維標號顯示效果十分理想，它不僅美觀、立體感強，并且顯示效果與二維標號幾乎一模一樣，這也讓其更容易被理解和使用。

圖9 二維態勢標號效果

4 結束語

本文對三維標號的生成方法進行了研究，提出以二維標號算法庫為基礎生成三維標號的方法，該方法關鍵在于如何將二維繪制基礎圖元轉化成三維繪制基礎圖元。由于二維標號算法庫已經封裝了標號差異，這讓本文的三維標號在生成時不必關心標號類型，從而極大地減少了三維標號制作生成的復雜性。同時，因為使用的是基于矢量數據的繪制方式，這也表明運用本文方法生成的三維標號非常便于日后的交互編輯工作。

圖10 三維態勢標號效果

本文還需要進一步研究的工作包括三維標號中相鄰圖元在銜接處的處理以及如何提高線面標號與地形匹配的效率。

［1］YANG Qiang，CHEN Ming.Real-time creating and protracting of 3D static unit symbols［J］.Computer Engineering and Design，2007，28(14):3419-3421(in Chinese).［楊強，陳敏.三維靜態軍標的實時生成與標繪 ［J］.計算機工程與設計，2007，28(14):3419-3421.］

［2］YU Meijiao，ZHANG Yongsheng，DAI Chenguang.Implement of rendering situation symbol over 3D Terrain ［J］.Jounal of Geomatics，2008，33(4):40-42(in Chinese).［于美嬌，張永生，戴晨光.實現復雜態勢符號在三維場景中的繪制［J］.測繪信息與工程，2008，33(4):40-42.］

［3］OpenSceneGraph ［EB/OL］.http://www.openscenegraph.net.

［4］WANG Jiarun，ZHAO Nansong，Hua Wenyuan，et al.Construction of cubic Bezier continuous subsection curve's control points［J］.Computer Engineering and Applications，2010，46(22):190-193(in Chinese).［王家潤，趙南松，華文元，等.分段連續三次Bezier曲線控制點的構造算法［J］.計算機工程與應用，2010，46(22):190-193.］

［5］De Berg M.Computational geometry algorithms and applications［M］.2nd ed.DENG Junhui，transl.Beijing:Tsinghua University Press，2006:50-72(in Chinese).［計算幾何-算法與應用［M］.2版.鄧俊輝，譯.北京:清華大學出版社，2006:50-72.］

［6］CHEN Hong，TANG Xiaoan，YANG Yaoming，et al.Using display mapping for irregular military symbols rendering［J］.Journal of Computer-Aided Design and Computer Graphics，2011，5(23):798-803(in Chinese).［陳鴻，湯曉安.基于位移映射的非規則軍隊標號繪制算法 ［J］.計算機輔助設計與圖形學報，2011，5(23):798-803.］

［7］JIANG Huawen.Design and implementation of 3D military symbol based on B-Spline［D］.Jilin:Jilin University，2009:42-34(in Chinese).［姜華文.基于B樣條的三維軍隊標號的設計與實現［D］.吉林:吉林大學，2009:32-34.］

［8］XIAO Bin，WANG Jinshu.Research and implementation of 3D campaign situation display at sea［J］.Journal of System Simulation，2008，14(20):3746-3749(in Chinese).［肖濱，王金樹.海上戰役態勢三維顯示的研究與實現［J］.系統仿真學報，2008，20(14):3746-3749.］

［9］WANG Rui，QIAN Xuelei.OpenScene Graph 3D rendering engine and practise［M］.Beijing:Tsinghua University Press，2009:90-127(in Chinese).［王銳，錢學雷.OpenSceneGraph三維渲染引擎設計與實踐 ［M］.北京:清華大學出版社，2009.90-127.］

［10］XU Zemin，HE Jun.Design and realization of 3D graphics simulation system for battlefield situation［J］.Journal of Computer Applications，2009，29(6):313-316(in Chinese).［徐澤敏，何軍.戰場態勢三維圖形仿真系統的設計與實現［J］.計算機應用，2009，29(6):313-316.］

［11］XIAO Peng，LIU Gengdai，Xu Mingliang.OpenSceneGraph 3D rendering engine programming guide［M］.Beijing:Tsinghua U-niversity Press，2010:289-307(in Chinese).［肖鵬，劉更代，徐明亮.OpenSceneGraph三維渲染引擎編程指南［M］.北京:清華大學出版社，2010:289-307.］

［12］Donald Hearn，Pauline Baker M.Computer graphics with OpenGL［D］.3rd ed.CAI Shijie，transl.Beijing:Electronic Industrial University Press，2006:216-242(in Chinese).［Donald Hearn，Pauline Baker M.蔡士杰，等譯.計算機圖形學［D］.3版.北京:電子工業大學出版社，2006:216-242.］