基于剃齒修形的嚙合角數值計算

蔡安江 張振軍 阮曉光

西安建筑科技大學，西安，710055

0 引言

剃齒作為齒輪的精加工方法被廣泛地應用，但采用標準漸開線的剃齒刀加工的齒輪齒形常出現不同程度的“齒形中凹”現象，影響齒輪的承載能力、傳動品質和使用壽命［1］。剃齒刀正確修形是解決“齒形中凹”的有效途徑。目前常用的剃齒刀修形方法僅提供了實現剃齒刀反凹修形的工藝方法，而修形的具體位置是靠試切法逐步確定的，齒形誤差的控制能力與修形目標性較差。

筆者在歸納總結有關剃齒刀修形研究成果的基礎上，基于切削點切入壓力產生的差異［2］(剃齒時剃齒刀與被剃齒輪之間嚙合點數的變化導致)形成的“齒形中凹”，提出了“剃齒刀精確修形技術”［3］。該技術克服了現有剃齒刀修形工藝技術的不足，能通過計算確定剃齒刀修形的位置，有效地消除剃齒“齒形中凹”現象。該修形技術中，端面嚙合角是確定剃齒刀修形位置的關鍵，決定了消除“齒形中凹”的工藝效果，因此，端面嚙合角的最優解計算方法研究就成為剃齒刀精確修形技術推廣應用的關鍵。

1 嚙合角計算解析

剃齒加工時，剃齒刀與被剃齒輪相當于一對無側隙的交錯軸圓柱齒輪(螺旋齒輪)嚙合。對于交錯軸齒輪傳動嚙合角的計算，理論上沒有一個顯性的公式可以直接得到其嚙合角或漸開線函數值。

設被剃齒輪齒數為，法向模數為mn1，分度圓法向壓力角為αn1，分度圓螺旋角為β1，分度圓法向弧齒厚為n1，漸開線終止點曲率半徑為ρmax1，漸開線起始點曲率半徑為ρmin1，剃齒超越量為δ;剃齒刀齒數為z0，法向模數為mn0，分度圓法向壓力角為αn0，分度圓螺旋角為β0，分度圓法向弧齒厚為n0。

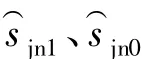
一對螺旋齒輪嚙合時，其節圓法向壓力角相等［4］，即 αjn=αjn1=αjn0，則式(1)可表示為

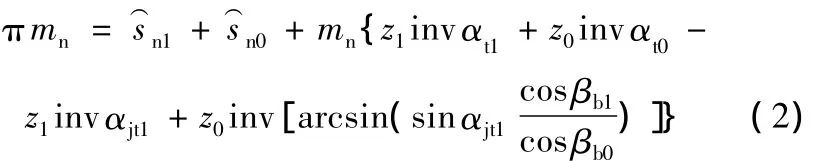
式中，mn為法向模數;inv(·)為漸開線函數;αt1、αt0分別為被剃齒輪和剃齒刀的端面壓力角;αjt1、αjt0分別為被剃齒輪和剃齒刀的節圓端面嚙合角;βb1、βb0分別為被剃齒輪和剃齒刀的基圓螺旋角。

式(2)是關于端面嚙合角αjt1計算的一階多維超越方程，無法直接求解，只能采用數值計算的方法求其最優解。令

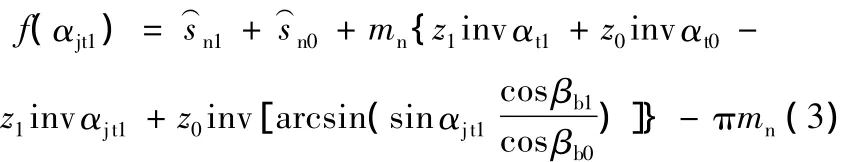
式(3)為一階多維非線性超越方程，存在求解時易出現數值解發散不收斂、求得的最優解精確度不高、可微性難以判斷等缺陷，因此，該類方程只能用數值計算的迭代法求解［5］。

2 嚙合角計算方法

目前，端面嚙合角普遍采用近似計算的方法［6］，但在嚙合角較小、節圓直徑與分度圓直徑差值較大或嚙合壓力角與分度圓壓力角差值較大的情況下，采用該方法計算所得的端面嚙合角就會產生較大的誤差。端面嚙合角決定了理論嚙合線長度計算的精確性，與剃齒“齒形中凹”現象有著密不可分的聯系［7］。

端面嚙合角的計算可以采用數值計算中的迭代法來獲得嚙合角的最優解。從而提高嚙合角計算的精確性，即可通過牛頓迭代法和史蒂芬森－牛頓類迭代法(S－N迭代法)來求得端面嚙合角的最優解。

2.1 牛頓迭代法

牛頓迭代法是目前求解超越方程較好的迭代法，具有求解精度較高、迭代次數較小的特點［8］。

將式(3)對αjt1微分得到 (αjt1)，采用牛頓迭代法通過有限次迭代，就可以求得滿足式(2)且可滿足精度要求的αjt1，由αjt1得出αjt0并可得到法向嚙合角:

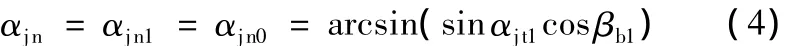
通過下式可以較精確地計算出理論嚙合線長度，從而準確得到剃齒刀的修形位置。

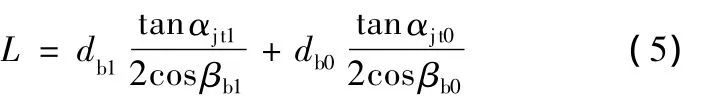
式中，db1、db0分別為被剃齒輪和剃齒刀的基圓直徑。

應用牛頓迭代法計算端面嚙合角的值時可精確到10－7rad，甚至更高。牛頓迭代法與目前普遍采用的近似計算相比，端面嚙合角的計算值在10－2就顯出差異。端面嚙合角計算值的誤差必然會導致剃齒刀修形位置的變化，使剃齒刀修形位置計算的有效性大大降低。

2.2 S－N迭代法

式(3)為復雜的一階多維非線性超越方程，為克服牛頓迭代法求解時需式(3)具備二階微分收斂的特性［9］，本文提出基于牛頓迭代法和史蒂芬森迭代法［10］的S－N迭代法，并將其用于端面嚙合角最優解的計算。

若f(x)在其零點x0處的領域內連續可微，并且 (x)≠0;假設xk為該方程的近似解，則根據牛頓迭代法公式可得

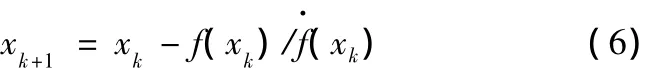
對式(6)應用歐拉法，可得

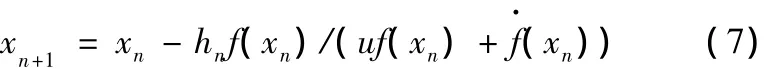
式中，u為修正系數，取值為0～1;hn為n次步長。

根據端面嚙合角的精確度要求，對式(7)中的u進行重新選擇，以使求解過程更穩定，數值解趨于最優解。

利用差商公式代替式(7)中的(xn)，就得到用于端面嚙合角計算的S－N迭代法公式:

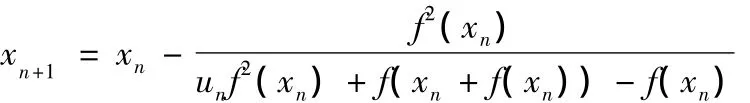
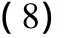
式中，un為第n次修正系數，取值為0～1。

式(8)用于嚙合角一階多維超越方程的求解時，克服了牛頓迭代法求解時要求在含根區間上(x)≠0及函數f(x)=0在其精確解x0的領域內連續可微的不足，并且可以根據嚙合角一階多維非線性超越方程的特點，不斷選擇修正系數μ，使求解過程更穩定，數值解趨于最優解。

S－N迭代法計算端面嚙合角時，式(8)中的修正系數μ越接近于0，數值解越趨于最優解，求解過程越穩定。μ＞0.45時，其迭代過程就會陷入發散不收斂的狀態，不利于端面嚙合角的數值計算。

3 嚙合角計算分析

數值計算迭代法的參數設置中，初始值、誤差容限、迭代次數會直接影響收斂速度和最優解的精確性。初始值的選擇直接決定著該迭代法是否能夠達到全局最優解;誤差容限的選擇決定了求解的精度要求。

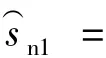
超越方程具有非線性，可以通過誤差容限判斷迭代過程的穩定性，通過迭代次數判斷迭代過程的快速性，通過數值最優解判斷求解的精確性。

3.1 誤差容限

誤差容限一般作為迭代計算的跳出準則。根據嚙合角一階多維超越方程的迭代特性和求解目的，將誤差容限取為10－4rad。從圖1、圖2可以看出:計算過程中，牛頓迭代法的嚙合角誤差大大超出了10－4rad，嚙合角誤差在計算區域內跳動很大，不穩定，在迭代157次后才達到收斂;S－N迭代法的嚙合角誤差相對穩定，在大多數計算區域內誤差跳動不大，具有穩定性，迭代至97次后就達到收斂。

3.2 迭代次數

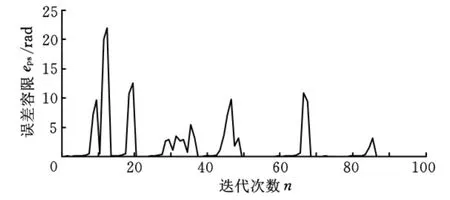
圖1 S－N迭代法誤差容限控制的跟蹤圖

圖2 牛頓迭代法誤差容限控制的跟蹤圖

求解超越方程時，迭代次數是很重要的衡量指標，一般要求較小的迭代次數就得出最優解。從圖3可以看出:采用S－N迭代法計算嚙合角時，嚙合角在大部分區域內波動較小，迭代至97次后，嚙合角就達到收斂，且在迭代至69次后已逐漸開始趨于最優解。從圖4可以看出:采用牛頓迭代法計算嚙合角時，嚙合角在大部分區域內波動較大，不利于嚙合角最優解的求解。在迭代至157次后才達到收斂，且在迭代至139次后才開始逐漸趨于最優解。因此，在嚙合角的計算中，S－N迭代法具有求解穩定、迭代次數較小等優點，同時也避免了求解一階多維超越方程需求導帶來的復雜運算。

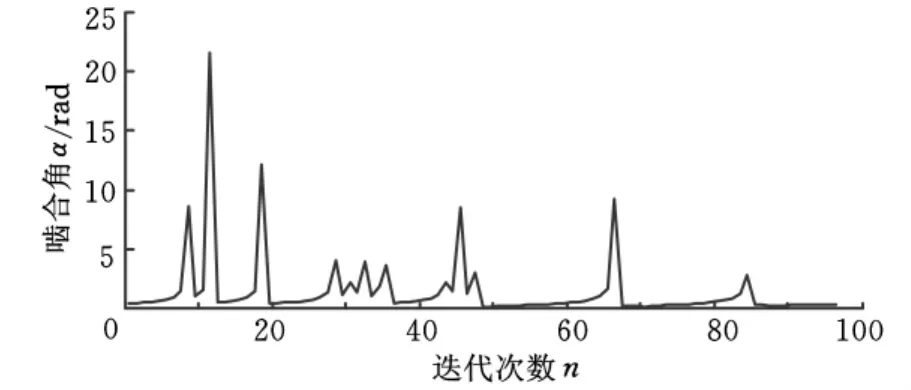
圖3 S－N迭代法嚙合角求解的跟蹤圖

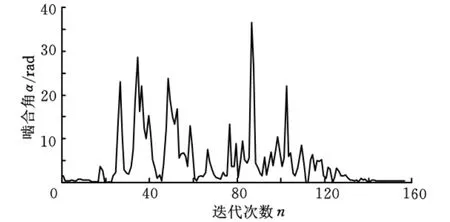
圖4 牛頓迭代法嚙合角求解的跟蹤圖

3.3 嚙合角最優解

根據剃齒加工經驗，可將算例嚙合角的初始值x0取0.3317rad［11］。采用S－N迭代法和牛頓迭代法計算嚙合角一階多維超越方程的結果如表1所示。S－N迭代法和牛頓迭代法在嚙合角計算過程中的總體趨勢基本一致，S－N迭代法的嚙合角計算結果更接近于其最優解(剃齒加工中的實際嚙合角)，而牛頓迭代法在嚙合角計算的迭代過程中，其近似解往往偏離最優解，且計算過程極易發散。因此，S－N迭代法在求解嚙合角一階多維超越方程中優于牛頓迭代法。

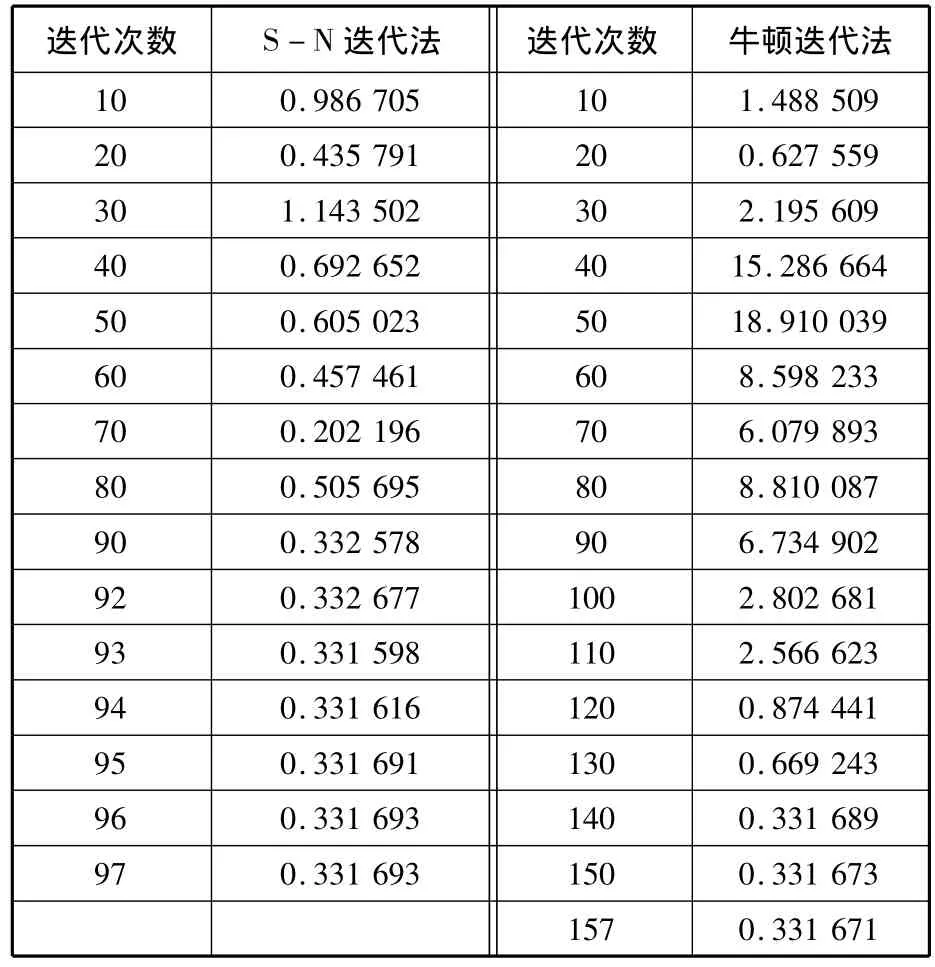
表1 兩種迭代法對嚙合角超越方程的計算結果 rad

應用S－N迭代法和牛頓迭代法計算嚙合角時可以得到最優解，提高了剃齒刀修形位置計算的準確性，修形后的剃齒刀在汽車變速箱齒輪、減速箱齒輪等生產中進行了工業生產試驗。結果表明:被剃齒輪的“齒形中凹”現象基本得到了消除，大大提高了被剃齒輪的齒形精度。

4 結論

(1)采用史蒂芬森－牛頓類迭代法和牛頓迭代法進行嚙合角的計算，可得到嚙合角的最優解，能避免端面嚙合角計算誤差導致的嚙合線長的計算誤差，提高了剃齒刀修形位置計算的有效性，保證了消除剃齒“齒形中凹”現象的工藝效果。

(2)在嚙合角的計算中，史蒂芬森－牛頓類迭代法比牛頓迭代法更接近于最優解，具有求解穩定、迭代次數較小等優點，同時也避免了求解一階多維超越方程時求導帶來的復雜運算。

(3)應用史蒂芬森－牛頓類迭代法求解嚙合角一階多維超越方程時，調整修正系數μ可以使求解過程更穩定，使數值解趨于最優解，從而有效地解決嚙合角計算精確性的技術難題。

［1］詹東安，吳序堂，孫景友，等.“剃齒刀隨機修形”的理論研究與試驗［J］.工具技術，1998，32(3):6-9.

Zhan Dong'an，Wu Xutang，Sun Jingyou，et al.Theoretical Study and Test of Shaving Cutter Random Modification［J］.Tool Technology，1998，32(3):6-9.

［2］王彥靈，林彤.用計算嚙合節點位置法進行剃齒刀中凹修形［J］.機械傳動，2001，25(4):51-53.

Wang Yanling，Lin Tong.Using the Method of Computing Mesh Nodes Location for Shaving Cutter Concave Modification［J］.Mechanical Transmission，2001，25(4):51-53.

［3］蔡安江，郭師虹，楊選文.一種對剃齒刀進行修形的方法:中國，ZL2005 1 0096129.8(P).2009-08-05.

［4］吳序堂.齒輪嚙合原理［M］.西安:西安交通大學出版社，2009.

［5］林成森.數值計算方法［M］.北京:科學出版社，2005.

［6］四川省機械工業局.復雜刀具設計［M］.北京:機械工業出版社，1979.

［7］彭娟媚，唐軍.提高圓柱齒輪剃齒加工質量與效率的方法［J］.工具技術，2006，40(8):90-94.

Peng Juanmei，Tang Jun.Methods of Improving the Processing Quality and Efficiency of Cylindrical Gear Shaving［J］.Tool Technology，2006，40(8):90-94.

［8］Atkinson K.Elementary Numerical Analysis［M］.Hoboken，NJ，USA:John Wiley ＆ Sons Inc.，1985.

［9］Wu Xinyuan，Wu Hongwei.On a Class of Quadratic Convergence Iteration Formulae without Derivatives［J］.Applied Mathematics and Computation，2000，107(2/3):77-80.

［10］Zheng Quan，Wang Jing，Zhao Peng，et al.A Steffensen － like Method and Its Higher－ order Variants［J］.Applied Mathematics and Computation，2009，214(1):10-16.

［11］胡敏.剃齒刀修形技術及其CAD系統的研究［D］.西安:西安建筑科技大學，2009.