薄壁管材矯直過程應變中性層偏移模型與分析

張子騫 楊會林 田永利

1.東北大學，沈陽，110004 2.天津大學，天津，300072

0 引言

近年來，高精度薄壁金屬管材在工業、軍事、醫療、航空航天、石油化工等領域中的需求急劇上升，為使管材具備理想的直線度和圓度，必須在出廠或使用前對其進行精整矯直。目前，薄壁管材的矯直生產一般通過人工經驗或反復試矯完成，生產效率較低、產品質量穩定性較差，且針對的理論研究尚少。基于經典管材矯直理論確定的工藝參數在生產實踐中，表現出矯直精度低、截面畸變，甚至無法對工件有效矯直，并不適合薄壁管材的矯直生產，因此亟待對薄壁管材的矯直機理和變形過程進行深入的理論研究。

薄壁管材的矯直是針對已彎曲的管材施加更大程度的反向彎曲來實現的，與管材彎曲理論相似，彎曲外側和內側之間存在一個應變中性層［1］。隨著彎曲變形程度的不斷增大，中性層將偏移管材中心層，對偏移量的解析及其對矯直過程影響的分析是后續深入研究薄壁管材矯直理論的基礎。目前，國內外針對中性層偏移問題的處理有兩種方法:一種是基于梁彎曲的工程理論，忽略中性層的偏移［2］;一種是由管材精彎理論建立的偏移模型，其理論基礎為平面應變條件下平板塑性彎曲的Hill理論［3-5］。這兩種方法在處理普通板材和管棒材的彎曲與矯直問題時具有較好的適用性，但不適合薄壁管材的矯直，同時這些模型對材料性能的變化不敏感。為此，本文針對薄壁管材的結構特點，確定了平面變形的應力應變關系，基于此對應變中性層的偏移量進行了解析，分析了其變化趨勢和對矯直過程的影響，為深入研究薄壁管材的矯直機理和變形過程提供理論依據。

1 基本假設

在建立中性層偏移模型時需引入以下假設:

(1)材料是均質、連續及各向同性的，忽略矯直變形區的Baushinger效應，即材料具有拉壓一致性，并認為應力中性層與應變中性層重合。

(2)任意垂直于中心軸的管材截面在矯直過程中始終為平面，且與中心軸保持垂直;相鄰兩截面間無傾斜扭曲，并忽略管材截面尺寸的變化。

(3)薄壁管材矯直變形過程中的塑性區域遵循體積不變原則。

(4)由于管壁很薄，故忽略管材矯直過程中的壁厚變化，同時徑向正應力遠小于其他應力，可忽略不計。

(6)矯直工作過程平穩，管材在工作輥面上做純滾動，在矯直輥縫內的變形區可視為等彎矩純彎曲過程［6］。

2 矯直變形分析

薄壁管材通常指管徑與壁厚之比遠大于20的管材，其在矯直過程中易出現起皺、扭曲和破裂等缺陷，為避免缺陷產生，通常采用減小單次反彎變形量，增加反彎次數的方法，一般采用8輥或10輥斜輥矯直機。工作輥分為上輥與下輥，在空間上交錯布置于管材兩側，與被矯直管材成一定夾角，如圖1所示［6］。具有初始曲率的管材依次通過中間各組具有等曲率輥形的矯直輥，進行連續彎曲變形實現矯直。

圖1 上下矯直工作輥空間布置

這里采用切塊法對薄壁管材在輥縫內的矯直變形區進行分析，與經典管材彎曲理論在圓柱坐標系下選取微元體的方法不同，管材在矯直時具有初始曲率，管殼表面為空間曲面，故這里選用空間子午坐標系，在輥縫內矯直變形區的任意位置取微元體單元ABCD，如圖2所示。該單元體由2個夾角為dθ的管材子午面與2個夾角為dφ的平行圓包圍而成，子午面與某一基準子午面夾角為θ，平行圓處的管殼表面法線與彎曲軸線夾角為φ，因管壁較薄，取微元體的厚度為管壁厚度t。同時規定任意一點的坐標方向如下:X軸方向為平行圓的切線方向，Y軸方向為管材子午線的切線方向，Z軸方向為管材外表面的法線方向。

薄壁管材的矯直變形與普通管材彎曲變形的相似之處:變形區以中性層為界，X方向外側材料主要受切向拉伸而伸長，內側材料主要受切向壓縮而縮短。

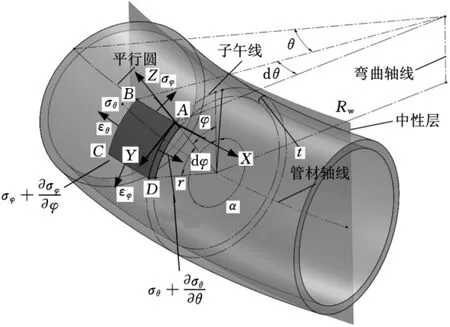
圖2 薄壁管材矯直區應力應變狀態模型

薄壁管材的矯直變形與普通管材的彎曲變形也有很大不同:在Z方向上，普通管材彎曲理論認為外側壁厚減小，內側壁厚增大;薄壁管材因壁厚較小，矯直工藝本身要求矯直前后壁厚基本無變化，故矯直變形程度相對較小，因此矯直過程造成的厚度變化是十分微小的，由假設(4)知，Z方向上的變形可忽略不計，即εr=0;同時Z方向上的正應力遠小于其他應力，有σr=0，故矯直區的三維應變狀態簡化為平面應變問題，則Z平面上的切應力分量 τθr=τφr=0，切應變分量 γθr=γφr=0。

薄壁管材的矯直與普通管材的彎曲的另一個重要區別是加工工藝不同。普通管材在彎曲時，沿軸線運動通過彎曲模，管材本身并不繞軸旋轉，因此分析時可將管材子午線切線方向即Y方向的應力與應變忽略;薄壁管材在圖1所示的空間交錯的工作輥中螺旋前進，管材除了沿軸線直線運動外，還繞Y軸旋轉，再者因管材厚度小，Y方向上抵御失穩的能力差，因此Y方向的應力與應變需要計入。同時，由于薄壁管材矯直變形程度相對較小，截面上橫剪力τθφ雖然存在，但由假設(2)、(6)可認為τθφ是足夠小量，而由橫向剪應變引起的橫截面任何變形可以忽略［7］，因此 τθφ=γθφ=0。

經上述分析，矯直變形區的應力應變狀態與相關幾何關系如圖2所示。其中，r為薄壁管材半徑，Rw為薄壁管材幾何中心軸反彎半徑，管材彎曲矯直時，沿彎曲切線方向(X向)作用的應力、應變為σθ和εθ，沿管材子午線切線方向(Y向)作用的應力、應變為σφ和εφ，彎曲應變中性層偏移角為α，t為管壁厚度。

3 矯直區彈塑性應力應變狀態

3.1 應力平衡微分方程

對微元體單元ABCD列寫應力平衡微分方程，在X方向上由于假設τθφ=0，因此

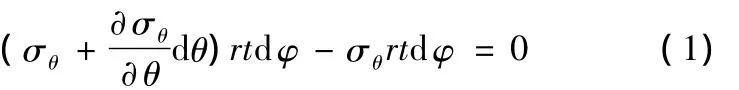
在Y方向上，考慮σφ的同時還要考慮σθ在Y方向上的投影，如圖3a所示，σθ在平行圓徑向的投影分量為σθrdφdθ，則該力在Y方向上的分量為 σθrdφdθcosφ，如圖3b所示。因此，對Y方向列寫應力平衡微分方程，有

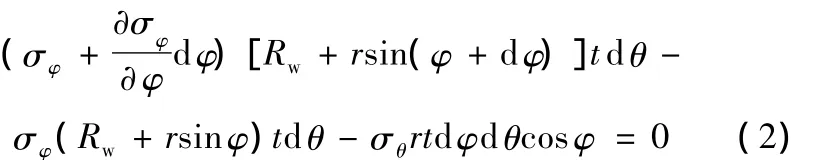
又因為 sin(φ+dφ)=sinφcosdφ+cosφsindφ ≈sinφ+dφcosφ，將其代入式(2)并化簡整理得

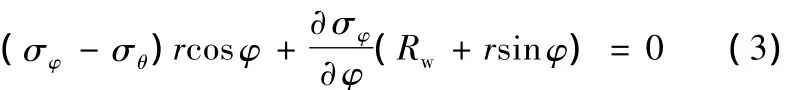
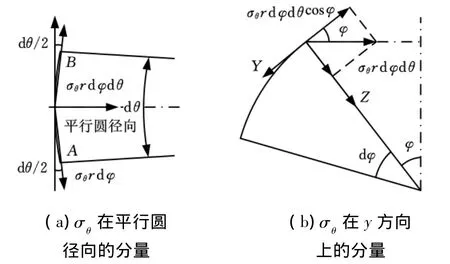
圖3 σθ的投影關系圖

Z方向上的正應力σr=0，因此不考慮該方向的應力平衡方程。

3.2 應變分析

薄壁管材具有初始曲率，故可假設微元體ABCD初始處于壓縮區，則反彎后微元體處于拉伸區。由于管壁較薄，若想實現矯直其初始彎曲程度不能太大，可認為矯直前薄壁管材的幾何中心軸與中性層重合，則管材的初始長度l0為

式中，R0為薄壁管材矯直前的初始曲率;θ0為薄壁管材矯直前的初始中心角。

微元體ABCD處初始纖維長度lφ0為

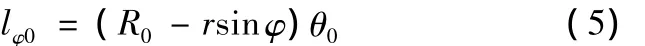
薄壁管材在矯直時需反向彎曲，中性層向彎曲軸向方向偏移α角，此時中性層的長度lw為

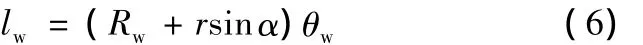
其中，θw為薄壁管材矯直時的反彎中心角，此時微元體ABCD處的纖維長度lφw為

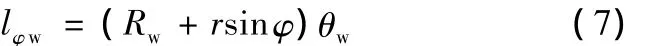
因此，Y方向的真應變為

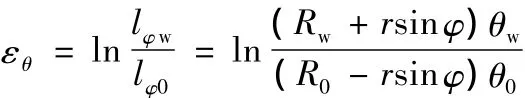
變形前后中性層的長度保持不變，矯直區的中性層長度等于管材初始長度，即

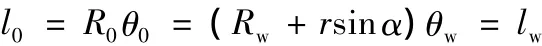
因此

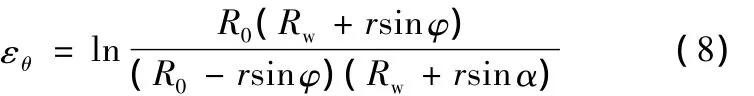
3.3 彈性區應力應變關系

為使薄壁管材得到矯直而截面形狀基本不變，必須保證中性層附近的某個區域為彈性變形區域。由于彈性變形區域較小，且彈性變形量通常較小，因此可認為彈性區內各變形層的初始長度均為管材的初始長度，則彈性區Y方向的真應變可近似表示為

在彈性區域中，金屬遵循線彈性變形的基本原理，其本構關系遵循廣義胡克定律:

其中，μ為泊松比，將式(10)代入式(9)得

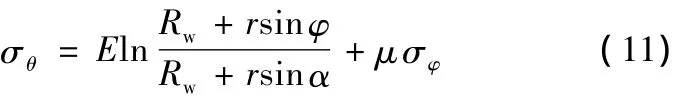
將式(11)代入式(3)并整理得

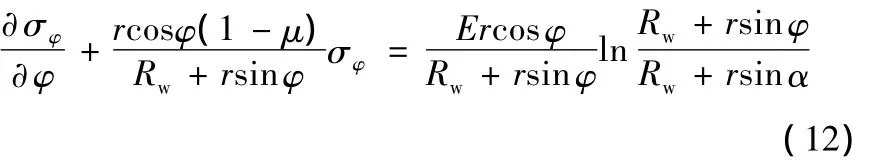
該一階線性非齊次微分方程的通解為

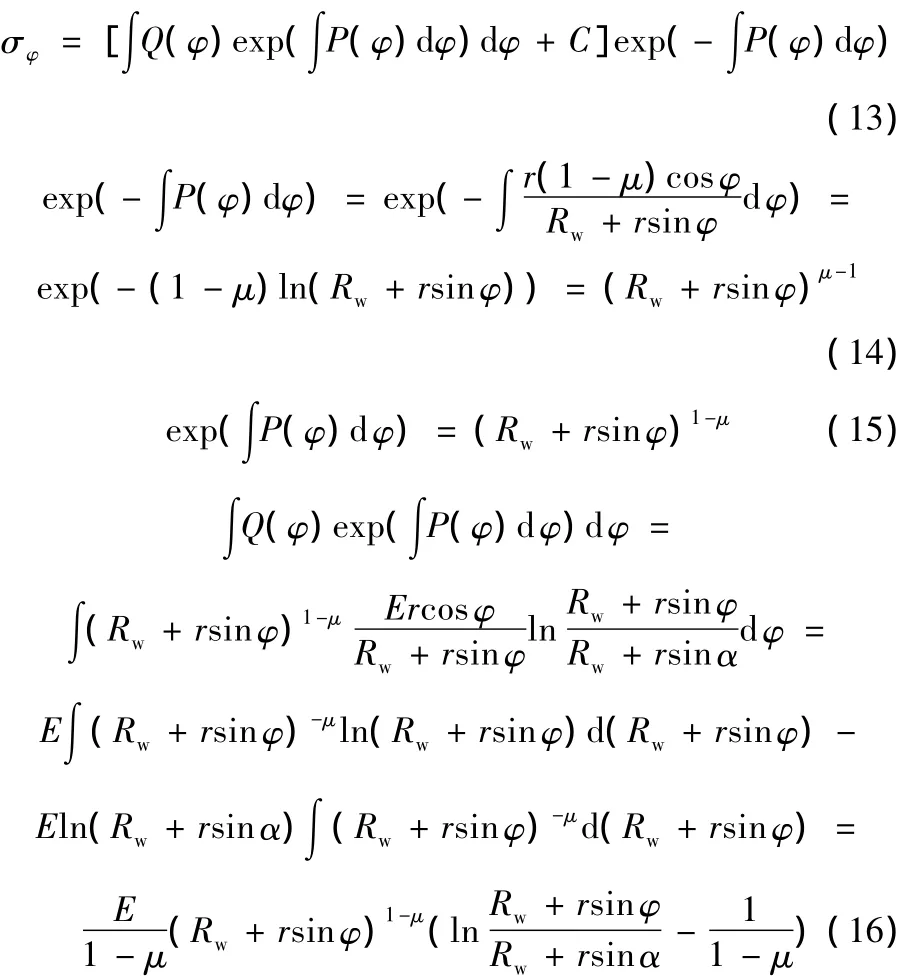
將式(14)～式(16)代入式(13)并化簡整理得

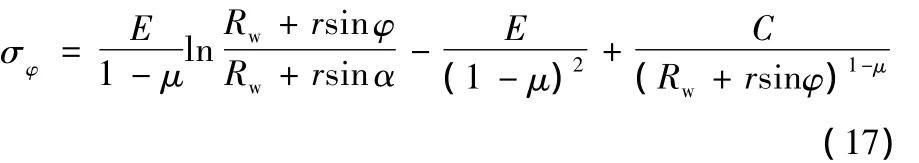
將式(17)代入式(11)并化簡整理得

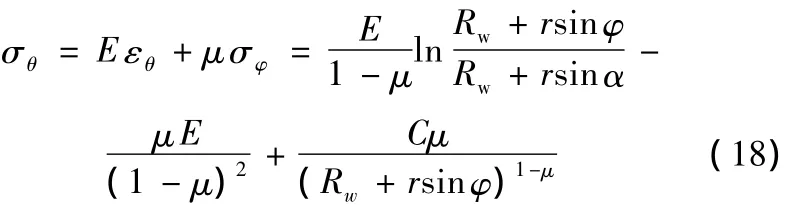
又由假設(1)可知，當φ=α時，σθ=0，將其代入式(18)可得

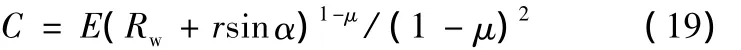
將式(19)代入式(17)、式(18)，得彈性區X、Y方向的主應力:

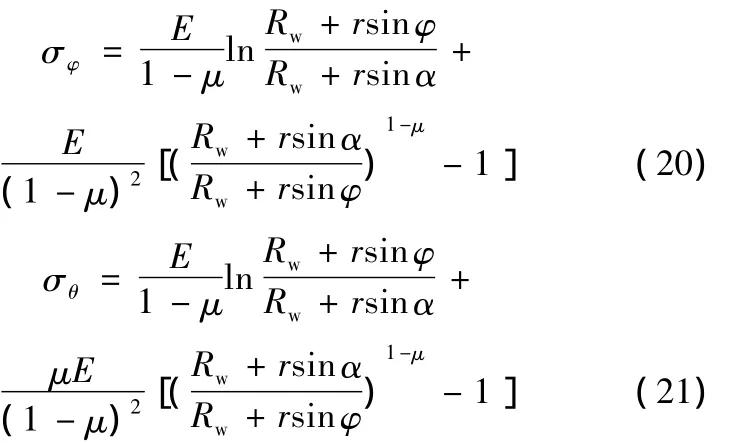
3.4 塑性區應力應變關系

薄壁管材在矯直過程中，除中性層附近的彈性區域外，其余均為塑性變形區域，遵循金屬塑性變形相關規律。由假設(3)知，在塑性變形區有εθ+εφ=0，則 εr=(εθ+εφ)/2。平面應變狀態下，由增量理論知σr=(σθ+σφ)/2。因此，塑性區的等效應力、等效應變為

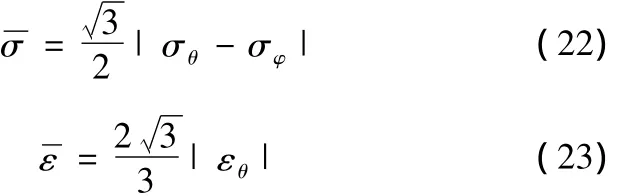
由假設(5)知

塑性變形相對于彈性變形而言，變形程度較大，故Y方向塑性應變由式(8)表示。將式(8)、式(22)、式(23)代入式(24)并整理得

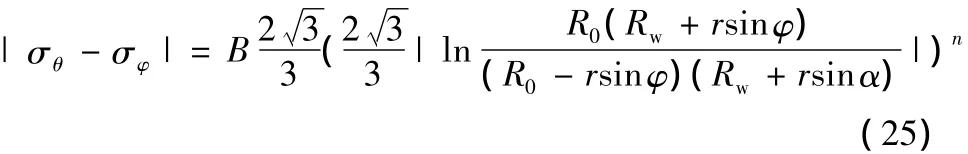
4 中性層偏移數學模型

薄壁管材在矯直過程中，彈性區域與塑性區域必然存在一個屈服分界面，當管材的變形量增大到一定程度，材料發生初始屈服，由假設(5)可知，彈性區的等效應力與等效應變的關系為

當彈性區外層發生初始屈服時，由Mises屈

服準則有

式中，σs為屈服應力。

將式(27)、式(26)代入式(28)得

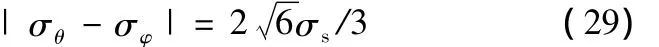
若此時屈服面偏移中心軸的角度為β，將式(20)、式(21)代入式(29)得

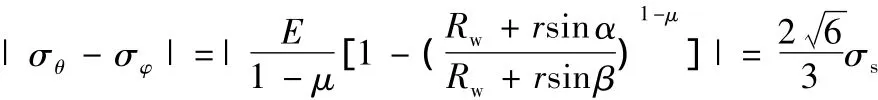
因此

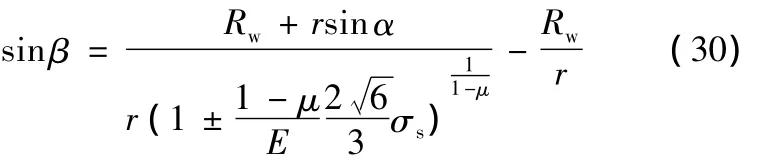
而對于塑性區的應力應變狀態，在初始屈服時同樣應滿足式(28)，即

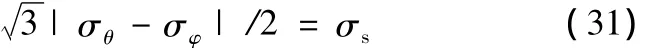
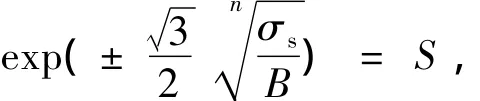
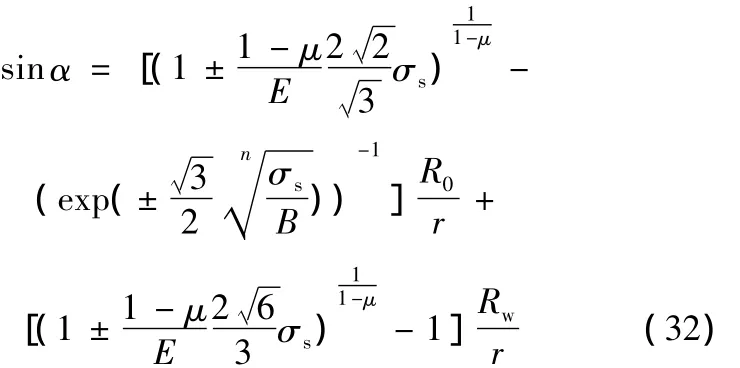
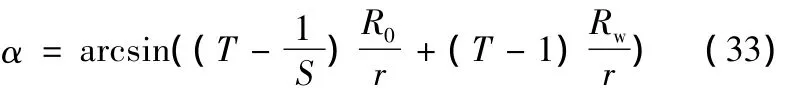
5 數學模型分析與仿真實驗

由式(33)可見，中心層偏移角α與薄壁管材的工藝結構參數(初始相對彎曲半徑R0/r、反彎相對彎曲半徑Rw/r)有關。通常，矯直工藝將來料管材的R0/r最大值規定為定值，這樣α便隨Rw/r的變化而變化;同時，α還與材料的力學性能有關，式(33)中的量綱一參數S、T就是由材料的力學性能決定的。不同金屬的力學性能與結構參數(薄壁管材半徑r=20mm，管材壁厚t=1mm)如表1所示［8-9］，計算了不同Rw/r下的偏移角值，如圖4的空心點所示;基于此擬合了α隨Rw/r的變化曲線，如圖4的實線所示。為驗證偏移模型的正確性采用ANSYS/LS－DYNA對典型材料的薄壁管材矯直變形過程進行了動態仿真，測量了相同條件下的中心層偏移角，在圖4中以虛線表示。

表1 不同金屬力學性能與結構參數表

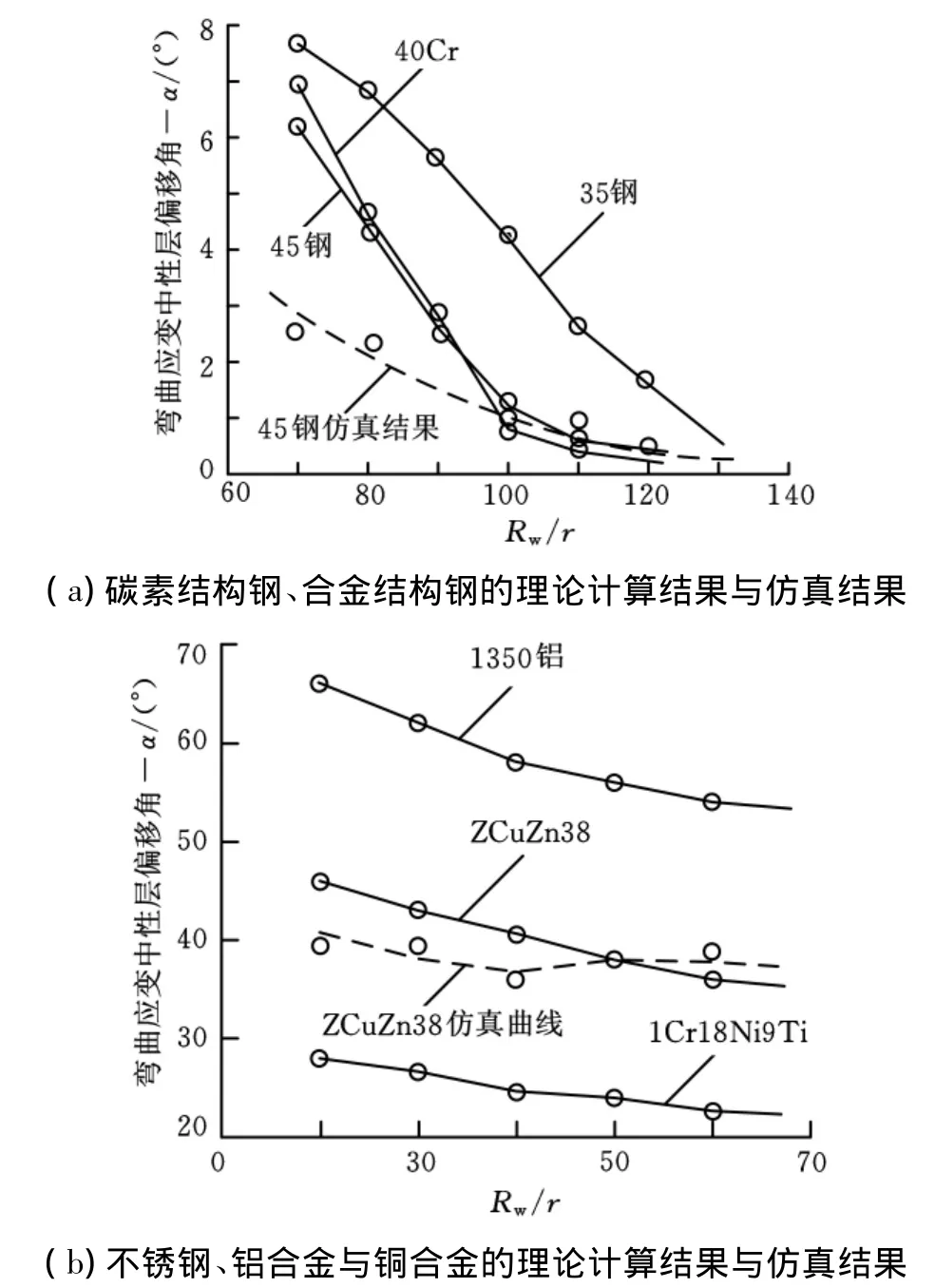
圖4 不同典型金屬材料薄壁管材α隨R w/r的變化曲線

由圖4可見，中心層偏移角的仿真實驗值與理論計算值存在一定差距，這主要是由仿真過程未計入管材的初始變形、建立有限元模型時網格劃分較大、理論計算模型并未涉及約束形式等原因造成的，但兩者差距并不是很大，基本控制在5°以內，同時仿真實驗值與計算值隨Rw/r的變化趨勢大體相同，因此可認為式(33)的計算結果近似準確。

由圖4可見，在R0/r一定的前提下，中心層偏移角α隨Rw/r的減小而增大，這說明當初始彎曲程度相同時，對于同一管材半徑，矯直反彎半徑越小，管材的變形程度越大，中性層向內偏移越大;對于同一反彎半徑，管材的半徑越大，中性層偏移越大，這些定性分析結果與文獻［3-4］得到的結果相似。

對比圖4a和圖4b可知，不同材料的薄壁管材在矯直時的偏移角相差很大，這說明α與材料的力學性能有關，材料的塑性越好，偏移程度越大，這是文獻［3-4］中模型所無法體現的。由圖4a可見，對于碳素結構鋼、合金結構鋼等材料的管材，由于材料塑性變形能力相對較弱，管材初始彎曲半徑較大，為防止管材在矯直過程中發生破壞，其反彎半徑也相對較大，因此中性層偏移較小，一般均在2mm以內，故在分析計算時可認為中性層不發生偏移。由圖4b可見，對于不銹鋼、鋁合金與銅合金等材料的管材，由于材料塑性變形能力相對較強，其初始彎曲半徑通常較小，若想實現矯直，其反彎半徑也相對較小，中性層偏移較大，故在分析計算時需考慮中性層的偏移。

上述分析僅針對普通規格薄壁管材的反彎矯直，并不適用于微小直徑及超大直徑薄壁管材的矯直與彈塑性彎曲。

6 結論

①本文建立的薄壁管材矯直過程的中性層偏移與相關理論模型，可對彈塑性變形區的應力應變狀態、初始屈服面與應變中性層位置進行理論估算與分析。仿真實驗證明，該理論模型是近似正確的，為進一步深入研究薄壁管材矯直機理和變形過程提供了理論依據。②薄壁管材矯直時，中心層的偏移量不僅與工藝結構參數有關，還與材料的力學性能有關，它隨相對反彎半徑的增大而減小，隨金屬塑性變形能力的增強而增大。③對于碳素結構鋼、合金結構鋼等材料的薄壁管材，矯直過程的中性層偏移量較小，在工程計算分析時可忽略不計;對于不銹鋼、鋁合金與銅合金等金屬材料，中性層偏移量較大，分析計算時必須考慮。④本文建立的理論模型及其方法可推廣應用到薄壁型鋼的矯直及相關領域的分析研究中。

［1］Stechpwicz F.Bending with Upsetting of Copper Tube Elbows［J］.Journal of Materials Processing Technology，2000，100:236-240.

［2］崔甫.矯直原理與矯直機械［M］.北京:冶金工業出版社，2002.

［3］鄂大辛，郭學東，寧汝新.管材彎曲中應變中性層位移的分析［J］.機械工程學報，2009，45(3):307-310.

E Daxin，Guo Xuedong，Ning Ruxin.Analysis of Strain Neutral Layer Displacement in Tube － bending［J］.Chinese Journal of Mechanical Engineering，2009，45(3):307-310.

［4］余同希，章亮熾.塑性彎曲理論及其應用［M］.北京:科學出版社，1992.

［5］Li Longyuan，Kettle R.Nonlinear Bending Response and Buckling of Ring－stiffened Cylindrical Shells under Pure Bending［J］.International Journal of Solids and Structures，2002，39:765-781.

［6］張子騫，張柏森，楊會林，等.管棒材等曲率矯直力模型可視化設計［J］.東北大學學報(自然科學版)，2012，33(3):409-413.

Zhang Ziqian，Zhang Baisen，Yang Huilin，et al.The Visual Design on the Force Model of Tubes and Bars Equal Curvature Straightening［J］.Journal of Northeastern University(Natural Science)，2012，33(3):409-413.

［7］王俊奎，張志民.鈑殼的彎曲與穩定［M］.北京:國防工業出版社，1980.

［8］成大先.機械設計手冊［M］.5版.北京:化學工業出版社，2009.

［9］劉鳴放，劉勝新.金屬材料力學性能手冊［M］.北京:機械工業出版社，2010.