相空間重構和參數統一求解的石油價格預測

孫善輝，李 鴻，張祖峰

1.宿州學院 智能信息處理實驗室，安徽 宿州 234000

2.宿州學院 數學與統計學院，安徽 宿州 234000

3.宿州學院 信息工程學院，安徽 宿州 234000

相空間重構和參數統一求解的石油價格預測

孫善輝1，2，李 鴻3，張祖峰2

1.宿州學院 智能信息處理實驗室，安徽 宿州 234000

2.宿州學院 數學與統計學院，安徽 宿州 234000

3.宿州學院 信息工程學院，安徽 宿州 234000

1 引言

石油作為一種主要能源，對一個國家政治穩定、經濟發展起著至關重要的作用，石油價格受到軍事、政治、經濟和外交等因素綜合影響，具有隨機性、突變性和混沌性等變化特點，因此石油價格預測一直是預測領域中的研究熱點[1]。

基于混沌理論的石油價格預測主要包括相空間重構和預測算法兩個重要內容，兩者相互聯系，相互影響，共同作用于石油價格預測模型的預測結果。為了提高石油價格預測精度，綜合考慮相空間重構和預測算法之間的內在聯系，本文提出一種基于相空間重構和預測算法參數統一求解的石油價格預測模型（PSR-LSSVM），并采用大慶石油價格數據對模型性能進行仿真實驗，以檢驗本文模型的可行性和優越性。

2 相關研究工作

石油價格已經被證明是一個低維的混沌時間序列[2]。相空空間重構是混沌時間預測的基礎，可以挖掘隱藏于混沌吸引子中的演化規律。相空間重構時，時間延遲(τ)和嵌入維(m)的選取至關重要，直接影響到后繼石油價格的預測精度[3]。對于參數τ和m的選取，目前主要有兩種思想：（1）τ和m分別、單獨求解。如首先采用自相關法、互信息法等來確定τ，然后采用G-P方法、偽最近鄰域法等來確定m，然而自相關法僅能提取時間序列間的線性相關性；互信息法雖能反映出系統的多種整體性關系，但這些關系只是高維相空間在二維空間中的投影，僅反映出重構相空間中相鄰兩重構坐標的獨立性，而不能保證所有重構坐標間的整體獨立性。且在大多數的方法中，為了確定最佳的τ，需要先確定m，而為了確定m又需事先固定τ，這必將造成矛盾[4]。（2）τ和m統一求解。如Broomhead等提出了時間窗口法；Kim等提出的C-C法，τ和m統一求解利用τ、m間的相互關系，使重構后的石油價格時間序列更加準確反映石油價格變化趨勢，因此當τ、m常采用統一求解的思想[5]。當前，石油價格預測算法主要采用神經網絡和支持向量機等機器算法[6-7]，由于最小二乘支持向量機（LSSVM）具有訓練速度快，泛化能力優異等優點，因此本文選擇LSSVM作為石油價格預測算法，而LSSVM預測性能與其參數的選擇密切相關[8]。在基于LSSVM的石油價格預測預測模型中，其預測精度由相空間重構和LSSVM共同確定，但目前石油價格預測沒有考慮兩者之間的聯系，完全割裂兩者之間的內在聯系，導致τ和m的選取與LSSVM參數不匹配，難以建立整體性能最優的石油價格預測模型。

3 相空間重構和最小二乘支持向量機

3.1 相空間重構理論

設時間序列{xi}，其時間間隔為?t（單位時間），那么對于n個變量的動力系統有：

通過消元法，使其變換為一個n階非線性微分方程：

變換后，新軌跡為：

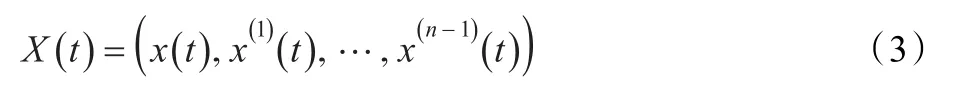
式（3）描述了與原時間序列同胚的動力學系統，它由x(t)加上 (n-1)階導數 x(1)(t)，x(2)(t)，…，x(n-1)(t)構成的相空間重組，代替這種連續變量x(t)和它的導數，并可考慮不連續的時間序列和它的 n-1時滯位移

只要將時間延遲τ選作時間序列的時間尺度，將會保證延滯坐標線性無關。

設單變量時間序列為{x(ti)，i=1，2，…，n}，時間延遲為τ=k?t，k=1，2，…，則可將該時間序列延拓成 m維相空間：

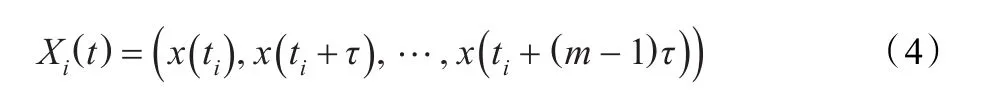
式中，Xi(t)為m維相空間中的一個相點。

任一相點Xi(t)有m個分量，m滿足條件：

m維相空間中的一個相點表示系統在某個瞬時后的狀態，而相點的連線構成了點在相空間中的軌跡，這條“軌線”便表示了系統狀態隨時間的演化。于是在m維相空間中得到了一個相型，原則上講，就有了足夠的信息把時間序列的動態特性展現在多維相空間上來進行考察[9]。

根據Takens定理，由合適的嵌入維數m和時間延遲τ重構的相空間，其在嵌入空間中的“軌線”與原系統是動力學等價的，因此有：

式中，T為預測步長，f()為重構的預測模型。

根據式（6），可以通過已知時間序列求出滿足式（6）的f()，就可以得到一個預測模型。

3.2 最小二乘支持向量機

對于訓練樣本集{(xi，yi)}，i=1，2，…，n，xi和 yi分別表示樣本輸入和輸出，通過非線性映射函數Φ()將樣本映射到高維特征空間，從而獲得最優線性回歸函數：

式中，w為特征空間的權值向量，b為偏置量。

根據結構風險最小化原則，式（7）問題求解的LSSVM回歸模型為：

式中，γ為正則化參數；ei為誤差。

通過引入拉格朗日乘子將式（8）轉變為對偶空間優化問題，即

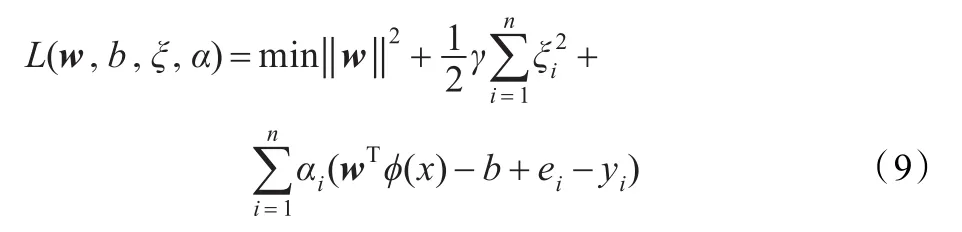
式中，αi為拉格朗日乘子。

根據Mercer條件，核函數定義如下：

選擇RBF核函數作為LSSVM核函數，RBF核函數定義如下：

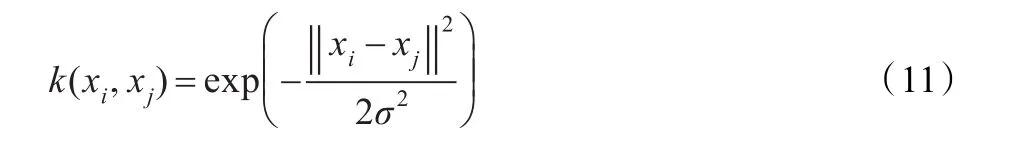
式中，σ為核函數寬度[10]。

最后LSSVM回歸模型為：

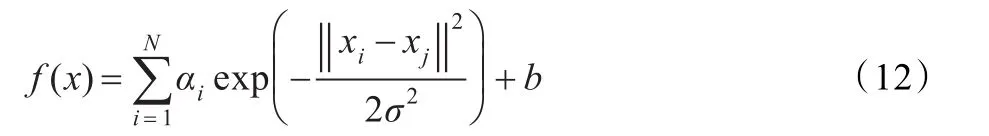
在LSSVM建模過程中，參數γ、σ對預測結果產生影響，當前LSSVM算法均沒有考慮γ、σ和τ、m間的聯系，建立的預測模型存在一定的缺陷。為了克服該缺陷，本文提出τ、m和γ、σ的統一求解思想。

4 石油價格預測模型參數統一求解

τ、m和γ、σ的統一求解是一個多參數組合優化問題，遺傳算法（GA）具有智能性搜索、并行式計算和全局優化等優點的仿生算法能夠在較短時間找到全局最優解[11]，因此本文采用GA算法對τ、m和γ、σ進行統一求解。

4.1 個體編碼設計

為了便于進行交叉和變異操作，GA的個體采用二進制編碼，每一個體包括τ、m和γ、σ四部分。由于個體采用二進制編碼，在進行石油價格預測與建模時，通過式（13）將參數轉換為十進制數。

式中，p表示參數的十進制值；pmin和 pmax表示參數的最小值和最大值；l表示個體二進制長度；d表示參數的二進制位串的十進制值。

4.2 適應度函數設計

粒子的優劣通過適應度函數值來評價，相空重構和預測算法參數統一求解目標是提高石油價格的預測精度，因此采用石油價格預測精度作為粒子的適應度函數，即有：

式中，accuracy表示在參數τ、m和γ、σ下的石油價格預測精度。

4.3 石油價格預測模型參數統一求解過程

（1）收集石油價格時間序列數據，由于LSSVM對0到1之間的數據最為敏感，因此對石油價格進行歸一化預處理，具體為：

最后需要對石油價格預測結果進行反歸一化處理，恢復真實預測值，具體公式如下：

（2）采用隨機方法產生初始化種群，每一個體由τ、m和γ、σ四部分組成。

（3）對個體進行反編碼，根據τ和m對石油價格時間序列進行重構，LSSVM根據參數γ、σ石油價格時間序列訓練集進行學習，建立相應的石油價格預測模型，計算每一個體的適應度值。

（4）判斷是否滿足算法的結束條件，若滿足結束條件，則停止優化，并對最優個體對進行反編碼，得到最優的τ、m和γ、σ，并轉至步驟（6）。

（5）對個體進行選擇、交叉、變異等遺傳操作，產生下一代種群，返回步驟（3）對參數繼續進行優化。

（6）根據最優參數τ、m重構石油價格時間序列，LSSVM采用γ、σ對石油價格訓練集進行學習，建立最優的石油價格預測模型，并對測試集進行預測，得到石油價格預測結果。

石油價格預測模型的建立流程如圖1所示。

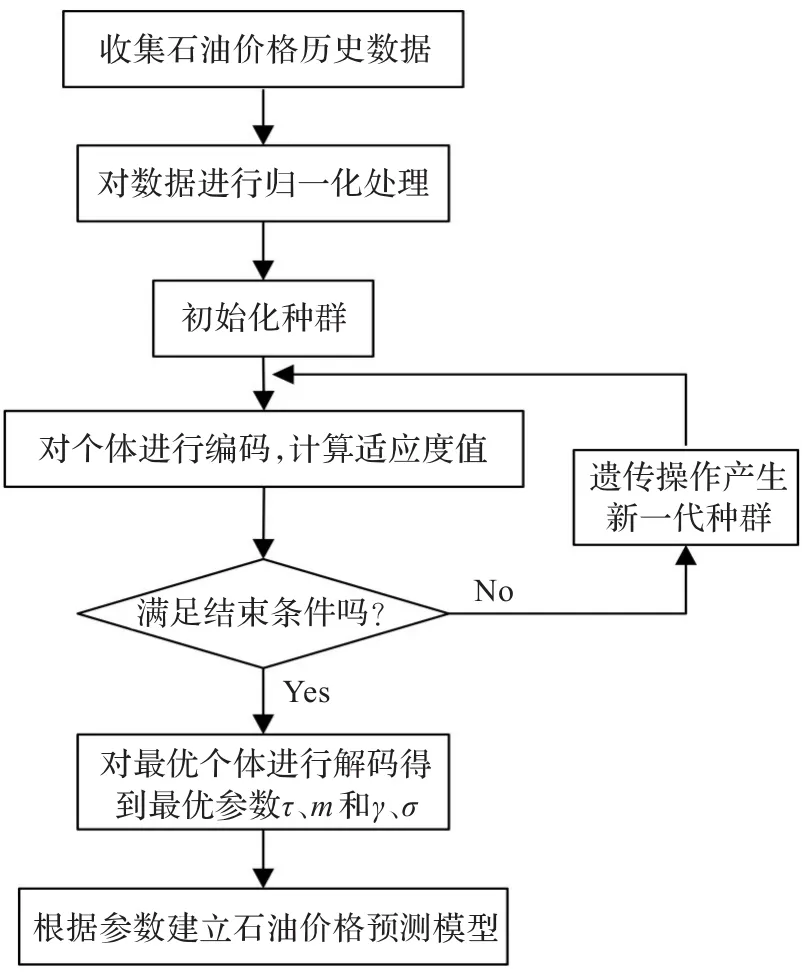
圖1 石油價格預測模型建立流程

5 仿真實驗

5.1 數據來源

采用2001年1月31日至2013年4月30日的大慶石油月平均價格作為仿真對象，共收集到160個數據，它們組成石油價格時間序列如圖2所示。前100個數據作為訓練集，后60個數據作為測試集。

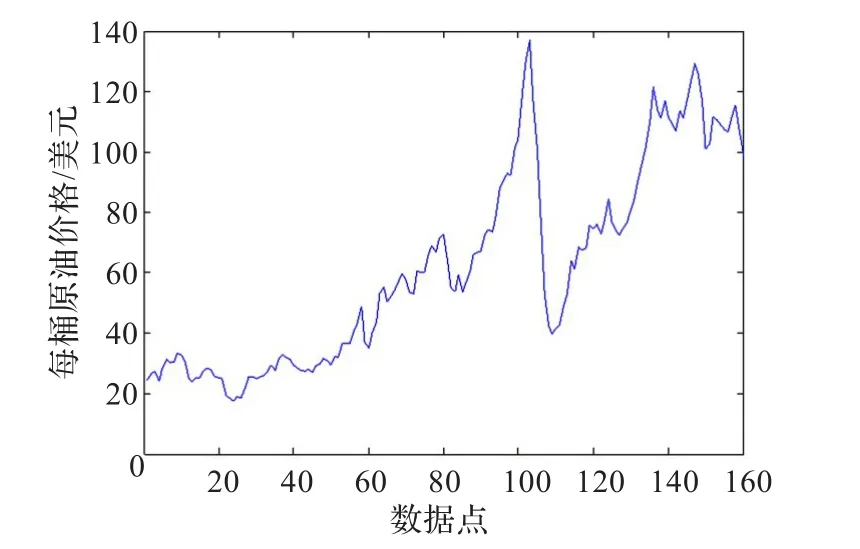
圖2 石油價格時間序列

5.2 對比模型及評價標準

為了使PSR-LSSVM的石油價格預測模型的結果具有可比性，選擇兩種對比模型，分別為：（1）互信息法和虛假鄰點法分別求解τ、m，GA優化LSSVM參數γ、σ的石油價格預測模型（LSSVM）；（2）首先采用C-C求解τ、m，然后采用GA優化LSSVM參數γ、σ的石油價格預測模型（CC-LSSVM）。采用均方誤差（RMSE）、平均相對百分比誤差（MPAE）作為模型預測結果優劣的評價標準。

5.3 模型實現

5.3.1 LSSVM的建模過程

對于圖2的石油價格時間序列，采用互信息法求其互信息函數，取其第一個極小值點作為延遲時間，由圖3可知，當τ取3時，得到第一個極小值，此時τ即為時間延遲。

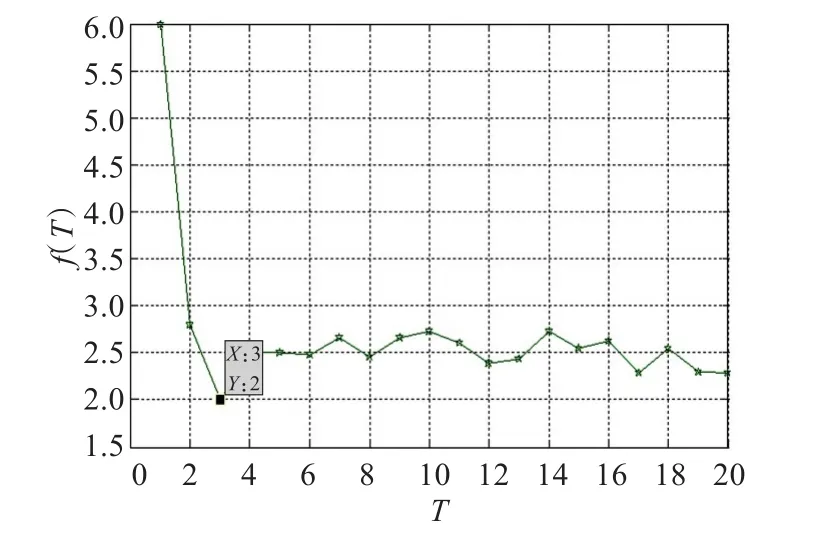
圖3 互信息法求時間延遲

通過虛假最近鄰點法求嵌入維數，結果如圖4所示，所求嵌入維數為4。用小數據量法計算大慶石油月平均價格時間序列的最大Lyapunov指數為1.163，表明大慶石油月平均價格時間序列具有混沌性。

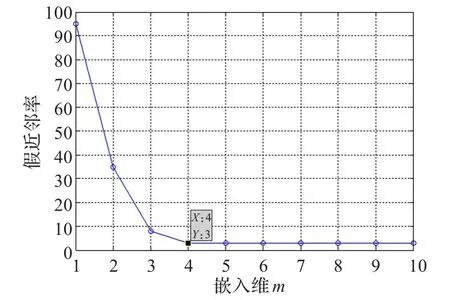
圖4 虛假鄰點法求嵌入維數

根據τ=3，m=4對石油價格時間序進行重構，然后將重構的石油價格時間序列訓練集輸入到LSSVM進行學習，采用GA對γ、σ進行優化，得到最優的γ=20.12，σ=1.43，從而建立基于LSSVM的石油價格預測模型。

5.3.2 CC-LSSVM的建模過程

對于石油價格時間序列，使用CC方法進行相空間重構。圖5為C-C方法計算延遲時間τ，從圖中可以看出，?Sˉ(t)的第1個近似極小值是4，Sˉ(t)的第1個近似零點也是4，于是確定延遲時間τ=4作為石油價格時間序列的時間延遲。

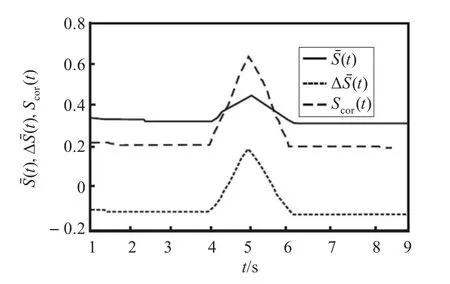
圖5 C-C法計算石油價格時間序列的時間延遲

圖6給出了采用C-C方法計算石油價格時間序列的Scor(t)曲線，可以看出Scor(t)大約在t=18時取得全局最小點，依據τw=(m-1)τ，因而取m=4。

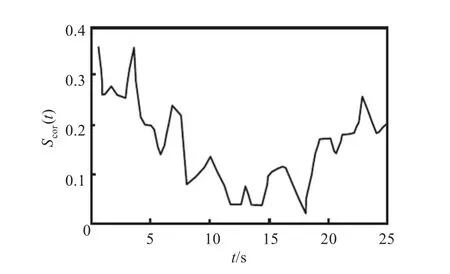
圖6 C-C法計算石油價格時間序列的Scor(t)曲線

根據τ=4，m=4對石油價格時間序列進行重構，然后將重構的石油價格時間序列訓練集輸入到LSSVM進行學習，采用GA對γ、σ進行優化，得到最優的γ=147.55，σ= 1.55，從而建立基于CC-LSSVM的石油價格預測模型。

5.3.3 PSR-LSSVM的建模過程

根據上述石油價格預測模型參數統一求解過程，得到PSR-LSSVM的最優參數為：τ=1，m=5，γ=176.45，σ=6.22，根據最優參數，建立基于PSR-LSSVM的石油價格預測模型。從而得到3種石油價格預測模型的參數見表1。

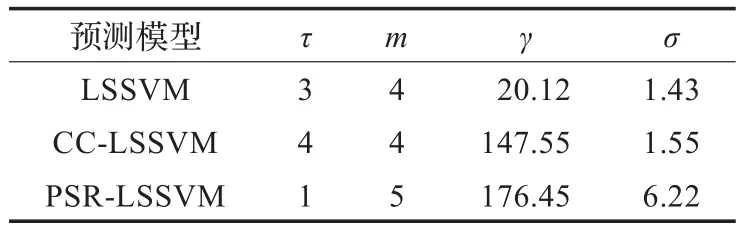
表1 石油價格預測模型的參數

5 .4 結果與分析

5.4.1 模型的泛化能力對比

根據建立的LSSVM、CC-LSSVM和PSR-LSSVM預測模型對石油價格訓練集進行擬合，得到的擬合結果如圖7所示。

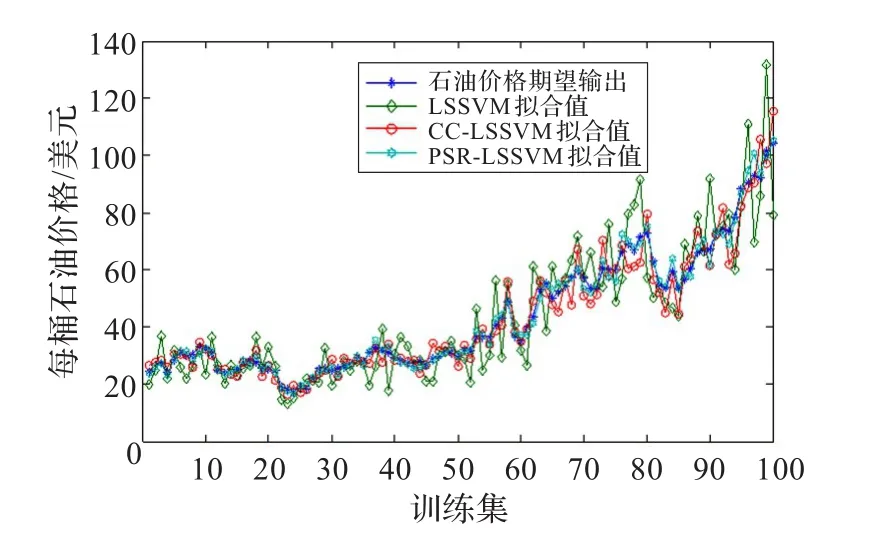
圖7 各模型對石油價格訓練集擬合結果

從圖7可知，在所有預測模型中，PSR-LSSVM的擬合效果最好，其擬合結果與石油價格期望輸出相當吻合。這主要是由于PSR-LSSVM通過對相空間重構的參數τ，m與LSSVM的參數γ，σ進行統一求解，挖掘了相空間重構和LSSVM之間的內在聯系，可以更加準確地擬合石油價格復雜的變化趨勢，進一步提高了石油價格擬合精度，對比結果表明，將PSR-LSSVM用于石油價格建模的思想是可行的、有效的，性能明顯優于τ，m與γ，σ分別、單獨優化的石油價格預測模型。

5.4.2 模型的泛化能力對比

評價一個預測模型性能的優劣，主要考察其預測能力而非擬合能力，因此，分別用LSSVM、CC-LSSVM和PSR-LSSVM的石油價格預測模型對測試集進行預測，得到的預測結果如圖8所示。從圖8可知，PSR-LSSVM的預測性能要優于對比模型，預測結果與實際石油價格值更加吻合，是一種預測精度高、泛化能力強的石油價格預測模型。

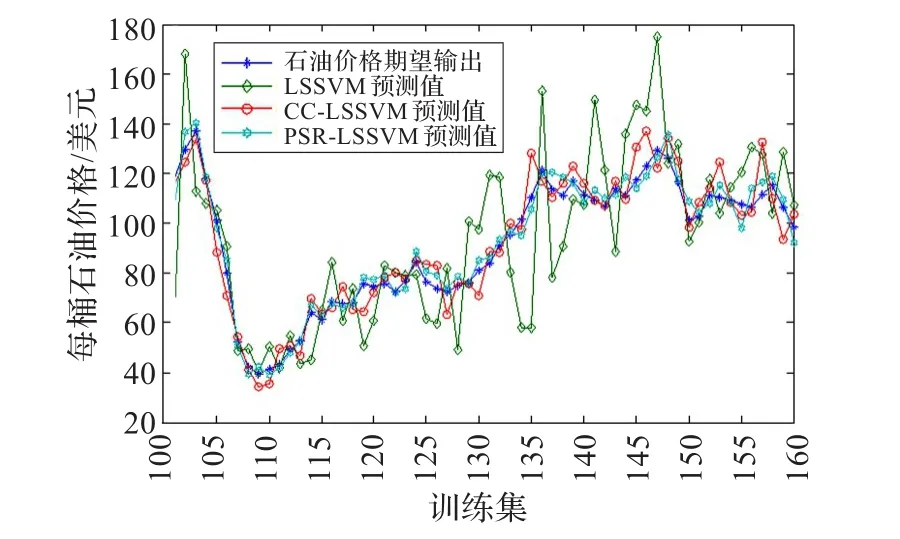
圖8 各模型對石油價格測試集的預測結果

各種模型的預測擬合和預測誤差見表2。從表2各種評價標準可知，PSR-LSSVM預測結果誤差遠遠小于LSSVM和CC-LSSVM，預測精度得以提高，綜合對比結果表明，PSR-LSSVM對相空間重構和預測算法參數進行統一求解，可以提高石油價格的預測精度，克服傳統分開、單獨優化難以找到全局最優參數的缺陷，預測結果更加可靠。

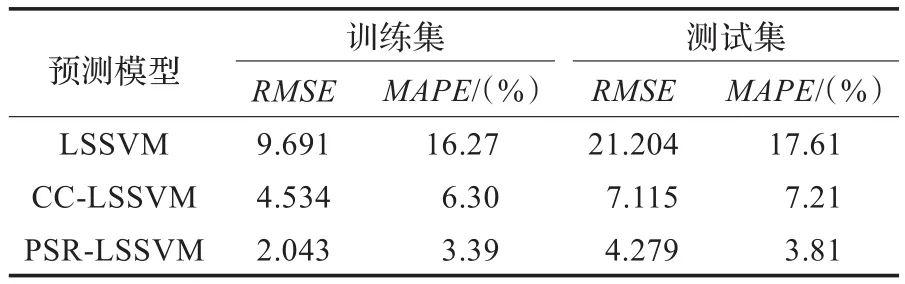
表2 不同石油價格預測模型的性能對比

6 結束語

石油價格具有時變性、混沌性，在石油價格建模預測過程中需要對相空間進行重構和對預測算法的參數進行優化，為此，充分利用兩者之間的聯系，挖掘出石油價格復雜的變化趨勢，提出了一種基于PSR-LSSVM的石油價格預測模型。仿真實驗結果表明，相對于對比模型，PSR-LSSVM提高了石油價格預測精度，研究成果對于具有混沌特性的石油價格建模和預測具有重要的理論和實踐意義。

[1]杜光年，劉志斌.石油價格波動分析與預測方法研究[D].長沙：湖南大學出版社，2006.

[2]朱小梅，郭志鋼.石油價格預測算法的仿真研究[J].計算機仿真，2011，28（6）：361-364.

[3]葛根，王洪禮，許佳.小波分頻技術和混沌時間序列在國際石油價格預測中的應用[J].系統工程與理論實踐，2009，29（7）：64-69.

[4]馬紅光，李夕海，王國華.相空間重構中嵌入維和時間延遲的選擇[J].西安交通大學學報，2004，38（4）：335-338.

[5]張春濤，馬千里，彭宏.基于信息熵優化相空間重構參數的混沌時間序列預測[J].物理學報，2010，59（11）：7623-7629.

[6]Farooq M，Mahdi N.Forecasting output using oil prices：a cascaded artificialneuralnetwork approach[J].Journalof Economics and Business，2006，58（2）：168-180.

[7]吳虹，尹華.ARIMA與SVM組合模型的石油價格預測[J].計算機仿真，2010，27（5）：264-266.

[8]陳帥，朱建寧，潘俊.最小二乘支持向量機的參數優化及其應用[J].華東理工大學學報：自然科學版，2008，34（2）：278-282.

[9]祝金榮，何永秀.基于混沌理論和支持向量機的電價預測[J].華東電力，2008，36（5）：16-20.

[10]劉立霞，馬軍海.基于LS-SVM的石油期貨價格預測研究[J].計算機工程與應用，2008，44（32）：230-231.

[11]Huang C L，Wang C J.A GA-based feature selection and parametersoptimization forsupportvectormachines[J]. Expert Systems with Applications，2006，31：231-240.

SUN Shanhui1，2,LI Hong3,ZHANG Zufeng2

1.Laboratory of Intelligent Information Processing,Suzhou University,Suzhou,Anhui 234000,China
2.College of Mathematics and Statistics,Suzhou University,Suzhou,Anhui 234000,China
3.College of Information Engineering,Suzhou University,Suzhou,Anhui 234000,China

In order to improve the predicting accuracy oil price,a novel oil price predicting model is proposed based on unified solving parameters phase space reconstruction and predicting algorithm according to relation between phase space reconstruction and predicting algorithm.The least square support vector machine is selected as the predicting algorithm of oil price,and the parameters of phase space reconstruction and LSSVM are taken as individuals of the genetic algorithm,and the optimal delay time,embedding dimension and LSSVM parameters are obtained through selection,crossover and mutation evolutionary mechanism,the predicting model of oil prices is established and the performance of predicting model is tested by Daqing oil price time series.The results show that the proposed model obtains higher predicting accuracy than the models which phase space reconstruction and LSSVM are optimized independently,and it provides a new research idea for the predicting problem of chaotic time series.

oil price;least squares support vector machine;phase space reconstruction;unified solving;modeling and predictions

為了提高石油價格預測精度，利用相空間重構和預測算法參數之間的相互聯系，提出一種基于相空間重構和預測算法參數統一求解的石油價格預測模型（PSR-LSSVM）。選擇最小二乘支持向量機作為石油價格預測算法，將相空間重構和LSSVM參數作為遺傳算法的個體，通過選擇、交叉和變異等進化機制找到最優的時間延遲、嵌入維和LSSVM參數，根據最優參數建立石油價格預測模型，并通過大慶石油價格時間序列對模型性能進行測試。結果表明，相對于獨立優化相空間重構和LSSVM參數的石油價格預測模型，PSR-LSSVM獲得了更高的石油價格預測精度，為具有混沌性的時間序列預測問題提供了一種新的研究思路。

石油價格；最小二乘支持向量機；相空間重構；統一求解；建模預測

A

TP391

10.3778/j.issn.1002-8331.1308-0068

SUN Shanhui,LI Hong,ZHANG Zufeng.Oil price predicting based on unified solving by phase space reconstruction and parameters.Computer Engineering and Applications,2013,49（23）：247-251.

安徽省高校優秀青年人才基金項目（No.2012SQRL202）；宿州學院智能信息處理實驗室開放課題（No.2013YKF15）。

孫善輝（1979—），男，講師，主要研究領域為分形幾何及其應用；李鴻（1965—），男，博士生，教授，主要研究領域為數據挖掘、算法設計與分析；張祖峰（1979—），男，博士，講師，主要研究領域為分數階微分方程。

2013-08-07

2013-09-23

1002-8331（2013）23-0247-05