三向四次箱樣條曲面與Bézier曲面的光滑拼接

楊聯強，王 東

安徽大學 數學科學學院，合肥 230601

三向四次箱樣條曲面與Bézier曲面的光滑拼接

楊聯強，王 東

安徽大學 數學科學學院，合肥 230601

1 引言

箱樣條（Box Spline）理論由de Boor和DeVore[1]開創，它以B樣條和Bézier方法為其特例，將單變量樣條推廣到多元樣條。在不同次數和定義域剖分方法的箱樣條中，三向四次樣條曲面由于其次數和連續階之間良好的均衡（四次，C2連續），從而得以廣泛重視和應用。著名的Loop細分曲面就是將三向四次箱樣條曲面從正規三角控制網格推廣到自由三角控制網格得到的。根據Stam[2]的網格參數化方法，Loop細分曲面的極限曲面幾乎處處是三向四次箱樣條曲面。

樣條曲面適合于大范圍連續曲面的構造，而Bézier曲面在設計單片曲面時卻非常實用。Bézier方法形式簡潔、性質優良，是計算機輔助設計（CAD）、計算機圖形學（CG）中的基本工具[3]。實際應用中，需要在用樣條曲面表示的大范圍曲面上，添加局部的小曲面片，或用小曲面片“來補洞”[4]，此時，兩曲面之間的光滑拼接就成為必須考慮的問題。因此，當三向四次箱樣條曲面設計完成后，在其上添加Bézier曲面時，必須要考慮如何選取Bézier曲面的控制頂點以使得兩曲面能光滑拼接。

有關曲面光滑拼接問題的研究成果已比較豐富。Du、Schmitt[5]對Bézier曲面的兩片拼接及多邊拼接作了比較完整的研究。施錫泉、趙巖[6]討論了雙三次B樣條曲面的拼接條件。曲學軍、寧濤、席平[7]介紹了基于調整已有曲面邊界控制頂點的方法使得B樣條曲面間實現G0、G1連續的方法。郝茹、劉潤濤[8]給出了雙四次有理Bezier曲面G1光滑拼接的頂點與權因子的相容條件。張錦秀、檀結慶[9]研究了H-Bézier曲面的G0、G1連續的相容條件。但是，目前這方面的研究主要集中于同種類型的曲面片之間的光滑拼接，而對不同類型的曲面片的光滑拼接的研究比較少。三向四次箱樣條曲面與Bézier曲面光滑拼接的條件這一問題還未見有顯式結果。本文針對這一問題，以多項式的Blossom為工具，討論了在給定三向四次箱樣條曲面，要設計與之C0、C1、C2拼接的Bézier曲面時，Bézier曲面的控制頂點所要滿足的條件。

2 預備知識

關于三向四次箱樣條的一般理論，詳見文獻[1，10]。單片的三向四次箱樣條曲面可以表示為（如圖1）：

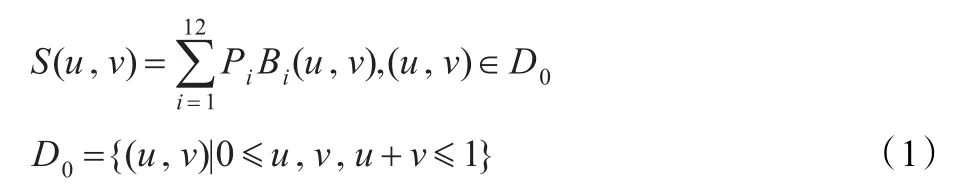
其中Pi是給定的?3中的十二個控制頂點，Bi(u，v)是參數化后的三向四次箱樣條基函數，其具體表達式可見文獻[2，10]。簡單計算可知三向四次箱樣條曲面具有：

性質1單片的三向四次箱樣條曲面是一張三邊的二元四次多項式曲面片，其在某一邊界上的0階、1階和2階導矢都是與鄰近該邊界的十個控制頂點有關，而與較遠的兩個控制頂點無關。

記定義在參數域?ABC上的n次三邊Bézier曲面為T(u，v)，控制頂點為Qijk，i+j+k=n。記定義在參數域[a，b]?[c，d]上的張量積型雙(m，n)次矩形Bézier曲面為R(u，v)，控制頂點為Rij，i=1，2，…，m;j=1，2，…，n，Bézier曲面具有：

性質2無論是三邊還是矩形Bézier曲面，其在某一邊界上的0階、1階和2階導矢，分別由與該邊界鄰近的一行、兩行和三行控制頂點決定，而與較遠的控制頂點無關。

由于本文考慮三向四次箱樣條曲面與Bézier曲面的光滑拼接，因此，取Bézier曲面的次數m和n都為4即可。

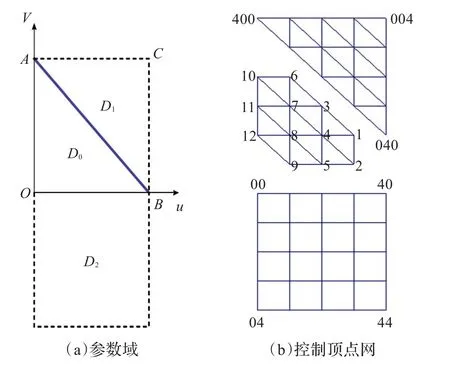
圖1 三向四次箱樣條曲面以及與其光滑拼接的三邊和矩形Bézier曲面的參數域和控制頂點網

3 給定三向四次箱樣條曲面，求與之光滑拼接的Bézier曲面

討論如下問題：

在參數平面?2上，給定由式（1）定義的三向四箱樣條曲面S(u，v)，設：

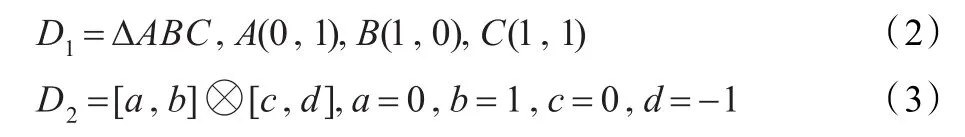
若定義在D1和D2上的T(u，v)和R(u，v)與S(u，v)分別C0、C1、C2拼接時，T(u，v)和R(u，v)的控制頂點應滿足什么樣的條件？

本文不采用通過分析兩參數曲面在共同邊界上的各階導矢相等，從而得到控制頂點的相容條件這一方法，因為這種方法整理出的表達式比較復雜。而是使用多項式的Blossom這一工具，簡潔巧妙地解決這一問題，直接給出由S(u，v)的控制頂點顯式表示的Bézier曲面的控制頂點。

多項式的Blossom（Polar Form）由Ramshaw[11]于20世紀80年代首次提出。之后，眾多學者利用這一方法對Bézier和B樣條方法作出了一種全新的精妙解釋，使得Blossom方法已成為研究Bézier和B樣條的強大工具[3-4，12]。二元多項式的Bézier形式的Blossom有兩種形式，分別在三角域和矩形域上進行，其具體的生成方法是用多元基本對稱多項式來代替原多項式中的冪項，過程簡單。在生成多項式的Blossom后，利用其對偶泛函性質，可以迅速求出該多項式在三角域和矩形域上的Bézier控制頂點。關于Blossom的生成及對偶泛函性質的應用，詳見文獻[4，12]。

下面給出解決問題的步驟：

首先，對已知的S(u，v)，這是一個二元四次多項式，分別生成它在三角域上的Bézier形式的Blossom，記作：

根據以上計算結果，得到如下定理：

定理1給定三向四次箱樣條曲面S(u，v)，若定義在D1上的三邊Bézier曲面T(u，v)的控制頂點滿足式（7），則T(u，v)與S(u，v)C0拼接，若滿足式（8）和式（9），則T(u，v)與S(u，v)C1拼接，若滿足式（7）、（8）和（9），則T(u，v)與S(u，v)C2拼接。

證明 只證明C2拼接的情況，C0和C1時的情況更簡單，不再贅言。

設想將多項式曲面S(u，v)的參數定義域延伸至區域D1上，記D1上的曲面部分Sˉ(u，v)：

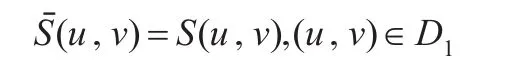
定理2給定三向四次箱樣條曲面S(u，v)，如果定義在D2上的矩形Bézier曲面R(u，v)的控制頂點滿足式（10），則R(u，v)與S(u，v)C0拼接，若滿足式（10）和式（11），則R(u，v)與S(u，v)C1拼接，若滿足式（10）、（11）和（12），則 R(u，v)與S(u，v)C2拼接。

根據以上結果，分別給出了實例（圖2、3、4）。中間位置曲面為三向四次箱樣條曲面，而兩側曲面分別為與之C0、C1、C2拼接的三邊和矩形Bézier曲面。

4 結論

以多項式Blossom為工具，給出了與三向四次箱樣條曲面光滑拼接的三邊或矩形Bézier曲面控制頂點的一個充分條件。當運用三向四次箱樣條曲面造型，而需要構造Bézier曲面與之光滑拼接時，該結果能直接使用，具有很好的理論和應用價值。

當Loop細分曲面的控制頂點網在邊界上沒有奇異點時，曲面的邊界即為三向四次箱樣條曲面，應用本文結果可以解決Loop細分曲面與Bézier曲面的光滑拼接問題。當Loop細分曲面的控制頂點網在邊界上有奇異點時，本文結果將不適用，此時，參照文獻[13]，基于網格細分的兩曲面間的光滑拼接問題的研究將是有意義的工作。

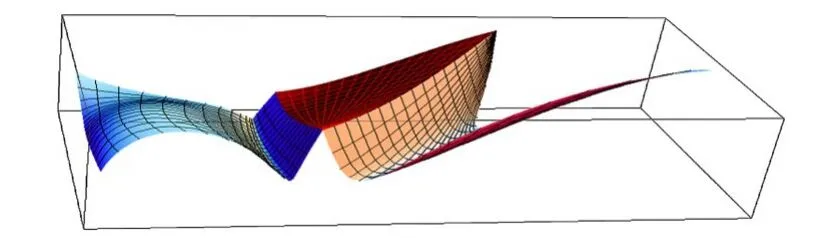
圖2 三向四次箱樣條曲面與Bézier曲面的C0拼接

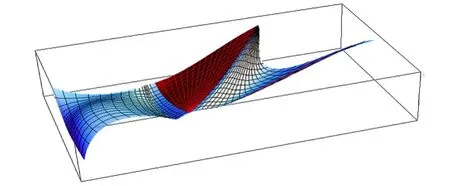
圖3 三向四次箱樣條曲面與Bézier曲面的C1拼接

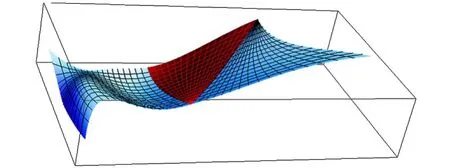
圖4 三向四次箱樣條曲面與Bézier曲面的C2拼接

[1]de Boor C，Hollig K，Riemenschneider S.Box spline[M].Heidelberg：Springer，1993.

[2]Stam J.Evaluation of Loop subdivision surfaces[C]//Computer Graphics Proceedings，Annual Conference Series，ACM SIGGRAPH，Orlando，1998：395-404.

[3]Farin G.Curves and surfaces in computer aided geometric design[M].5th ed.San Francisco：Morgan Kaufmann，2001.

[4]戈德曼.金字塔算法-曲線曲面幾何模型的動態編程處理[M].吳宗敏，譯.北京：電子工業出版社，2004.

[5]Du W H，Schmitt J M.On theG1continuity of piecewise Bezier surfaces：a review with new results[J].Computer-Aided Design，1990，22（9）：556-573.

[6]施錫泉，趙巖.雙三次B樣條曲面的G1連續條件[J].計算機輔助設計與圖形學學報，2002，14（7）：676-682.

[7]曲學軍，寧濤，席平.B樣條曲面的光滑拼接[J].計算機輔助幾何設計與圖形學學報，2004，16（1）：138-141.

[8]郝茹，劉潤濤.雙四次有理Bezier曲面G1光滑拼接算法[J].計算機工程與應用，2010，46（4）：174-200.

[9]張錦秀，檀結慶.H-Bézier曲面的分割與拼接[J].計算機工程與應用，2011，47（9）：152-155.

[10]Chui C K.Multivariate splines[M].Philadelphia：SIAM，1988.

[11]Ramshaw L.Blossoming：a connect-the-dots approach to splines[R].California：Systems Research Center，1987.

[12]Goldman R N.Polar forms in geometric modeling and algebraic geometry[J].Contemporary Mathematics，2003，334：3-24.

[13]韓越興，劉秀平，施錫泉.Loop細分模型的邊界拼接算法[J].大連理工大學學報，2004，4（1）：12-16.

YANG Lianqiang,WANG Dong

School of Mathematical Science,Anhui University,Hefei 230601,China

Using bivariate quartic polynomial’s Blossom over triangular and rectangular domains,when a 3-direction quartic box spline surface is given,in order to make triangular or rectangular Bézier surface to beC0、C1、C2connected with it,one kind of explicit sufficient condition of the Bézier surface’s control points which should be subjected is discussed.When geometric modeling with 3-direction quartic box spline surface or Loop subdivision surface,this conclusion is valuable for making Bézier surface to be smooth connected with the modeling surface or to fill holes.

3-direction quartic box spline surface;Bézier surface;smooth connection

以二元四次多項式在三角域和矩形域上的Bézier形式的Blossom為工具，給出了當給定一張三向四次箱樣條曲面時，能與之C0、C1、C2拼接的三邊或矩形Bézier曲面的控制頂點所要滿足的一個顯式表示的充分條件。這一結果在使用三向四次箱樣條曲面或Loop細分曲面造型，而又需要構造Bézier曲面與之拼接或補洞時，具有理論和實際應用價值。

三向四次箱樣條曲面；Bézier曲面；光滑拼接

A

TP391.7

10.3778/j.issn.1002-8331.1303-0387

YANG Lianqiang,WANG Dong.Smooth connection between 3-direction quartic box spline surfaces and Bézier surfaces. Computer Engineering and Applications,2013,49（23）：119-121.

國家自然科學基金數學天元基金項目（No.11026076）；安徽大學博士科研經費項目（No.31190016）；安徽大學本科生科研訓練計劃（No.KYXL20110003）。

楊聯強（1975—），男，博士，副教授，主要研究領域為計算機輔助幾何設計；王東（1991—），男，本科生。

2013-03-25

2013-05-30

1002-8331（2013）23-0119-03

CNKI出版日期：2013-08-27 http://www.cnki.net/kcms/detail/11.2127.TP.20130827.1603.014.html