直覺模糊集新的熵公式及應用

吳 濤，白禮虎，劉二寶，孫小慧

1.安徽大學 數學科學學院，合肥 230601

2.安徽大學 計算智能與信號處理教育部重點實驗室，合肥 230039

直覺模糊集新的熵公式及應用

吳 濤1，2，白禮虎1，劉二寶1，孫小慧1

1.安徽大學 數學科學學院，合肥 230601

2.安徽大學 計算智能與信號處理教育部重點實驗室，合肥 230039

1 引言

Zadeh[1-2]于1965年首次提出模糊集理論，又于1968年提出了模糊熵的概念。隨后De Luca和Termini[3]給出了在有限論域上模糊集熵的公理化定義。隨著模糊集的廣泛應用，Atanassov[4]對傳統的模糊集進行了拓展，提出了直覺模糊集的概念。Gau和Buehrer[5]又提出了Vague集的概念，這兩個概念在本質上是相同的。

Burillo P和Bustince H[6]最早引入了直覺模糊熵的概念，用來描述一個直覺模糊集的模糊程度。在此定義中，直覺模糊集的熵主要取決于不確定性的大小，又稱為“不確定性熵”，然而這個熵的定義與模糊集的熵之間不具有相容性。之后Eulalia Szmidt和Janusz Kacprzyk[7]提出了直覺模糊熵的新的公理化定義，在此定義中當直覺模糊集退化為模糊集時，滿足模糊集熵的公理化定義，但該直覺模糊集的熵主要取決于模糊性，不確定性考慮不足。

呂印超，郭嗣琮[8-9]分析了上面兩種定義的不足，指出直覺模糊熵應同時反映模糊性和不確定性這兩方面的影響，并給出了新的修改后的公理化定義，探究出了直覺模糊熵的一般形式，討論了模糊熵與測度之間的關系。然而，這個公理化定義仍然存在不足，在實際應用中出現失效甚至是矛盾的情況。另有學者范平[10]也考慮了這兩方面的影響同時提出了交叉模糊熵的概念。近年來，又有學者[11-12]研究了加權直覺模糊熵以及模糊熵的計算公式及其應用。

本文從文獻[8]中的公理化定義出發，用實例給出了其在應用中出現的問題，接著給出了新的修正后的直覺模糊集的熵的公理化定義，分析了修改的合理性，然后給出了基于新的公理化定義的直覺模糊熵的一個具體的計算公式，并對其進行了證明，最后給出了一個決策算法和應用實例。

本文中，記P(X)、F(X)、IFS(X)分別為論域X上分明集的全體、模糊集的全體、直覺模糊集的全體。

2 基本概念

定義2.1[4]（直覺模糊集）設 X是一非空集合，稱 A= {＜x，uA(x)，vA(x)＞|xX}為X上的直覺模糊集，其中uA(x)[0，1]，vA(x)[0，1]分別為 X中元素x屬于A的隸屬度和非隸屬度，且滿足條件0≤uA(x)+vA(x)≤1，?x∈X。

在上述定義中，若?x∈X，都有uA(x)+vA(x)=1，則直覺模糊集退化為模糊集。對于給定的 x∈X，稱πA(x)= 1-uA(x)-vA(x)為元素x屬于A的猶豫度或不確定度。記：

于是有πA(x)=1-hA(x)；若A是經典集合，則有| | sA(x)=1。

X中x屬于A的隸屬度和非隸屬度所組成的有序數對α=＜uA(x)，vA(x)＞稱為直覺模糊數。記：

為其得分函數。因此，可以將X上的直覺模糊集看作是直覺模糊數的集合。

定義2.2[8]（模糊度）稱：

為x在A中的模糊度。

在直覺模糊集中，隸屬度和非隸屬度從不同側面反映了集合元素的模糊性，而猶豫度反映了集合元素的不確定性。因而，直覺模糊集的熵應該綜合反映模糊性和不確定性這兩個方面的性質。在不確定性相同的情況下，若模糊性越大，則直覺模糊集的熵也越大，反之也成立。

3 直覺模糊集熵的公理化定義

Burillo P和Bustince H在文獻[6]中給出了直覺模糊集的熵的公理化定義。Eulalia Szmidt和Janusz Kacprzyk在文獻[7]中提出了直覺模糊熵的新的公理化定義。呂印超，郭嗣琮在上述定義的基礎上，綜合不確定性和模糊性兩方面的因素，在文獻[8]中提出了一個新的公理化定義。

定義3.1 ?A，B∈IFS(X)，隸屬函數分別為uA(x)和uB(x)，非隸屬函數分別為vA(x)和vB(x)，猶豫度分別為πA(x)和πB(x)。稱實函數 E:IFS(X)→R+為 IFS(X)上的熵，如果E滿足下列條件：

在文獻中對條件（P3）做了說明，條件（P3）等價于，?x∈X 若 πA(x)=πB(x)且 fA(x)≤fB(x)則 E(A)≤E(B)；若fA(x)=fB(x)且πA(x)≤πB(x)，則E(A)≤E(B)。

即當不確定性相同時，直覺模糊集熵的大小取決于模糊性；當模糊性相同時，直覺模糊集熵的大小取決于不確定性。

但是定義3.1在某些情況下會失效甚至出現矛盾的結果。請看下面一個例子。

例1設X={ }

x1，x2，在 X上有直覺模糊集：

則由定義3.1的（P2），若?x∈X有隸屬度和非隸屬度相等，則熵就等于1。如此E(A)=E(B)=1。又 fA(x1)=fB(x1)，πB(x2)=0.2＜0.4=πA(x2)。

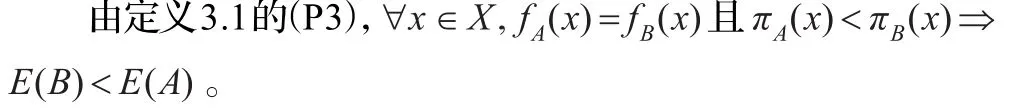
此時有兩個完全不同且矛盾的結果。

由上例分析可得，定義3.1中的條件是有問題的，需要進一步改進。根據分析可以提出如下新的公理化定義。

定義3.2設?A，B∈IFS(X)，隸屬函數分別為uA(x)和uB(x)，非隸屬函數分別為vA(x)和vB(x)，猶豫度分別為πA(x)和πB(x)。稱實函數 E:IFS(X)→R+為 IFS(X)上的熵，如果E滿足下列條件：

在上述定義中，修正了熵值取最大值的條件，即當隸屬度和非隸屬度相等且都為0。由于直覺模糊集的熵的大小取決于兩個方面的影響：模糊性和不確定性。模糊性越大，熵越大；不確定性越大，熵也越大，故當模糊性和不確定性都最大的時候才能取到最大值。當隸屬度和非隸屬度相等時，此時模糊性最大，進一步，若隸屬度和非隸屬度都相等且為0，此時不但模糊性最大，而且不確定性也最大，故而能取到熵的最大值。上述定義能很好地解決例1中的沖突。

例2設 A是有限論域 X={x1，x2，…，xn}上的直覺模糊集，Eulalia Szmidt和Janusz Kacprzyk在文獻[7]中構造的直覺模糊集的熵為：

式（3）在計算例2的情況時，會失效。此時有E(A)=E(B)=1，顯然不符合。基于此，可以提出如下的計算公式。

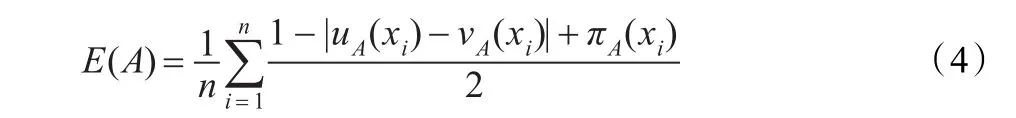
則E(A)是直覺模糊集A的模糊熵。

接下來用公式（4）再來處理例1中的情況：

比較結果有E(A)＞E(B)，完全滿足定義3.2中的條件（Q3），即模糊性相同的情況下，不確定性越大熵越大。

特別地，對于直覺模糊數 α=＜uA(x)，vA(x)＞，其模糊熵為：

相應地對于公式（3），其直覺模糊數的熵為：

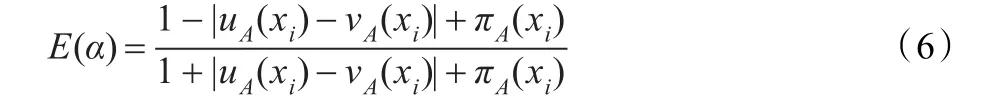
在式（6）中1-|uA(xi)-vA(xi)|=fA(xi)代表模糊度的大小，πA(xi)代表猶豫度的大小，且隨著 fA(xi)和πA(xi)的增大，模糊熵也在增大。故上式綜合考慮了模糊性和不確定性，而且計算起來更簡單有效。可以將式（4）做進一步的加權推廣，對模糊度和猶豫度進行加權。設w1+w2=1，0≤w1≤1，0≤w2≤1則有：

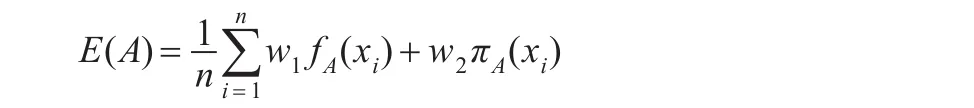
若論域 X是連續有界的，在[a，b]上存在直覺模糊集

4 基于直覺模糊數的熵的多屬性決策算法

步驟1對給出的直覺模糊集 Ai={＜ej，uAi(ej)，vAi(ej)＞| ej∈e}列出決策矩陣=(aij)n×m，其中aij表示第i個方案的第 j個屬性對應的直覺模糊數。

步驟2由公式（5），計算出直覺模糊數的熵，得出直覺模糊數的熵矩陣E=(eij)n×m。

步驟3將直覺模糊數的熵矩陣每行進行歸一化，得到歸一化矩陣=，則即為第i個方案的第 j個屬性的權重，記為

步驟4計算出綜合直覺模糊數

步驟5由式（1）計算出得分函數值 L(αi)，i=1，2，…，n根據計算出的得分函數值進行排序，L(αi)越大則對應的Ai方案越優。

5 實例分析

某房地產投資公司欲投資新建一處高端寫字樓，通過行業分析需考慮如下四個決策因素：區位因素(e1)，交通因素(e2)，資金因素(e3)，政策因素(e4)，假設對A1，A2，A3，A4各因素經統計后得到如下的直覺模糊數矩陣，如下所示：

將得分值排序：

方案A3為最優。

若將上述計算直覺模糊數的熵公式換為式（6），得到相應的得分值為：

將得分值排序：

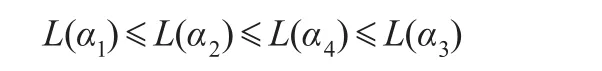
得出最優方案為A3。

比較兩種公式的計算結果，發現其具有較好的一致性，但是運用公式（5）得出的計算結果區分度更加明顯，計算過程也更為簡單，因而本文提供的計算公式也更為有效。

6 結束語

當前直覺模糊集的熵的公理化定義，在處理某些特殊情況時，存在一定失誤。本文在充分考慮不確定性和模糊性的基礎上，修正了公理化定義并給出了一個直覺模糊熵的新的計算公式，很好地解決了這一問題。最后通過應用此新的計算公式，給出了一種關于直覺模糊集的多屬性決策的有效解決方案。

[1]Zadeh L A.Fuzzy sets[J].Information and Control，1965，8（3）：338-353.

[2]Zadeh L A.Probability measures of fuzzy events[J].Journal of Mathematic Analysis and Applications，1968，23：421-427.

[3]De Luca A，Termini S.A definition of a nonprobabilistic entropy in the setting of fuzzy set theory[J].Inform and Control，1972，20：301-312.

[4]Atanassov K.Intuitional fuzzy sets[J].Fuzzy Sets and Systems，1986，20：87-96.

[5]Gau W L，Buehrer D J.Vague sets[J].IEEE Trans on SMC，1993，23（2）：610-614.

[6]Butillo P，Bustince H.Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets[J].Fuzzy Setsand Systems，1996，78（3）：305-316.

[7]Eulalia S，Kacprzyk J.Entropy for intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems，2001，118（3）：467-477.

[8]呂印超，郭嗣琮.直覺模糊集的熵及其一般形式[J].計算機工程與應用，2011，47（28）：52-55.

[9]呂印超，郭嗣琮.模糊熵、距離測度和相似性測度之間的關系[J].計算機工程與應用，2012，48（2）：36-38.

[10]范平.關于Vague集模糊熵的度量分析[J].計算機工程與應用，2012，48（1）：57-59.

[11]高志海，魏翠萍.一種區間直覺模糊熵公式及其應用[J].計算機工程與應用，2012，48（2）：53-55.

[12]吳成茂.一種加權直覺模糊熵分割法[J].計算機工程與應用，2011，47（34）：178-180.

WU Tao1，2,BAI Lihu1,LIU Erbao1,SUN Xiaohui1

1.School of Mathematical Science,Anhui University,Hefei 230601,China
2.Key Laboratory of Intelligent Computing&Signal Processing of Ministry of Education,Anhui University,Hefei 230039,China

With regard to the existing problems of axiomatic definition of entropy of intuitionistic fuzzy sets,a new revised axiomatic definition is given,then a new formula of entropy of intuitionistic fuzzy sets is proposed and proved.A multiple attribute decision making approach based on the entropy of intuitionistic fuzzy number is given,the effectiveness and rationality are verified by a practical example.

axiom definition;fuzziness;uncertainty;intuitionistic fuzzy set;entropy

針對直覺模糊集的熵的公理化定義中存在的問題，修正了直覺模糊熵的公理化定義，給出了一個新的直覺模糊集的熵的計算公式，證明了其正確性。給出了一個基于直覺模糊數的熵的多屬性決策算法，應用實例表明其合理性和有效性。

公理化定義；模糊性；不確定性；直覺模糊集；熵

A

TP391

10.3778/j.issn.1002-8331.1204-0692

WU Tao,BAI Lihu,LIU Erbao,et al.New entropy formula of intuitionistic fuzzy sets and its application.Computer Engineering and Applications,2013,49（23）：48-51.

國家自然科學基金（No.61073117）。

吳濤（1970—），男，博士，教授，主要研究方向：模糊決策、粒度計算；白禮虎（1986—），男，碩士研究生，主要研究方向：模糊決策和統計分析。E-mail：bailihu1117@163.com

2012-05-07

2012-07-09

1002-8331（2013）23-0048-04

CNKI出版日期：2012-08-01 http://www.cnki.net/kcms/detail/11.2127.TP.20120801.1652.019.html

◎網絡、通信、安全◎