整合供應商選擇的多層級選址-庫存模型

稅文兵，何保紅，何 民

昆明理工大學 交通工程學院，昆明 650500

整合供應商選擇的多層級選址-庫存模型

稅文兵，何保紅，何 民

昆明理工大學 交通工程學院，昆明 650500

1 引言

傳統的“先選址，再庫存”的順序決策方法，從總成本的角度來看，并不是最優的[1]。近年來，將選址分配決策問題和庫存控制決策問題進行整合，實現選址成本、運輸成本和庫存成本的平衡，從而進一步降低總成本，成為了物流系統優化的發展方向之一。基于選址分配決策和庫存控制決策的相互影響關系，從系統整體最優的角度，建立同時考慮選址成本、運輸成本和庫存成本的選址-庫存模型，對設施的位置、數量、服務范圍和庫存控制參數同時進行優化決策，在文獻中被稱為選址-庫存問題（Location-Inventory Problems，LIP）。

早在1958年，Baumol就提出應該在選址模型的目標函數中包含庫存成本[2]。文獻[1]建立了確定環境下基于經濟訂貨批量（EOQ）的連續選址-庫存模型，并采用微分方法求解，但是該模型沒有考慮設施的建立成本。文獻[3]研究了需求和提前期隨機變化下的選址-庫存問題，證明了當配送中心采用連續(S-1，S)補貨策略時，系統的總安全庫存與總配送中心數存在線性關系，并利用這種關系建立了線性的選址-庫存模型。然而，由于(S-1，S)庫存策略一般用于需求較少、提前期短的情況。對于需求量大的重要產品，往往采用(Q，R)庫存策略。因此，(Q，R)庫存策略下的選址-庫存問題成為了重要的研究方向。

文獻[4]針對由一個供應商、多個分銷中心和多個零售商的供應鏈，基于Axsater[5]的庫存成本計算方法，建立了第一個(Q，R)庫存策略下的選址-庫存模型。該模型較好地體現了選址分配決策和庫存控制決策之間的相互影響關系，從而成為了這一研究方向的基礎模型，得到了很多學者的進一步研究。如文獻[6]建立了基于場景規劃的模型，文獻[7]建立了考慮設施能力限制的模型，文獻[8]建立了考慮工廠選址的三層級選址模型等。這些研究從不同的角度完善了Shen的模型，然而，它們都只考慮了一個庫存點，沒有考慮多級庫存的情況。

除(Q，R)庫存策略下的LIP模型，其他庫存策略下的模型也得到了研究。文獻[9]針對連續檢查(Q，R)策略下的選址-庫存模型，會使每一個配送中心的訂貨間隔期都不相同，從而導致供應商在供貨時不能夠協調供貨，增加車隊的調度使用成本的問題，建立了配送中心采用定期檢查(T，S)策略下的選址-庫存模型。文獻[10]針對單供應商、配送中心和顧客構成的供應鏈，建立了配送中心采用(s，S)策略、顧客采用(R，S，Q)策略的多級選址-庫存模型，然而，模型沒有考慮不同庫存點之間的相互影響關系。文獻[11]基于Roundy[12]的多級庫存控制方法，建立了分銷中心和顧客都有庫存的選址-庫存模型，但仍然僅限于一個供應商的三層分銷網絡。文獻[13]基于EOQ模型假設和單點庫存控制策略，建立了允許供應商可以直接向顧客供貨的多級選址-庫存模型，然而，該模型沒有明確考慮空間距離對配送中心選址的影響。

上述研究有三個特點：（1）從供應鏈階段來看，大部分都只針對由工廠、配送中心和顧客構成的三級分銷網絡，沒有考慮零部件供應商的選擇；（2）從選址對象來看，都只對配送中心進行選址分配決策，沒有對工廠進行選址決策；（3）從所建立的模型特征來看，都是將選址分配模型和庫存控制模型融合為一個模型。前兩個特點決定了所建立的模型不能用于由供應商、工廠、配送中心和顧客組成的完整供應鏈網絡設計。最后一個特點使得所建立的模型呈現出高度的非線性，采用傳統的精確算法難以在較短時間內求解較大規模的問題。

在一個完整的供應鏈中，供應商的選擇、工廠和配送中心的選址、供應商與工廠以及工廠與配送中心之間的運輸量以及工廠和配送中心的庫存量都存在相互影響的關系。在進行這類供應鏈網絡設計和優化時，如果忽視了其中某個影響因素，所得到的設計方案從系統的角度看并不是最優的。本文針對由供應商、工廠、配送中心和顧客構成的四層級供應鏈網絡，構建同時對供應商的選擇、工廠和配送中心的選址和庫存控制參數進行決策的LIP模型。其中，利用梯級庫存概念，處理供應鏈中上下游庫存點之間的相互影響關系，建立工廠和配送中心的庫存成本計算模型。考慮到所建模型的復雜性，設計了基于部分編碼的粒子群優化算法求解，并通過多個算例驗證模型的有效性和算法的可行性。

2 模型建立

本文所研究的供應鏈網絡由供應商、工廠、配送中心和顧客組成，供應商向工廠提供原材料，工廠根據配送中心的訂單進行生產，產品生產出來之后通過配送中心運往顧客。配送中心通過成品庫存滿足若干顧客的確定需求，工廠分別通過原材料庫存和成品庫存滿足生產和配送中心的需要。在已知顧客的需求、單位運輸成本、候選的供應商、工廠和配送中心位置等參數下，對供應商的選擇、工廠和配送中心的選址、節點之間的運輸量，以及設施的庫存量進行決策。

2.1 模型參數和變量

基本參數：I為顧客的集合，某一個顧客用i表示；J為配送中心的集合，某一個配送中心用 j表示；P為工廠的集合，某一個工廠用 p表示；S為供應商的集合，某一個配送中心用s表示。di為顧客的需求（單位/年）；DDj為配送中心的需求（單位/年）；DPp為工廠成品倉庫的需求（單位/年）；DMp為工廠原材料倉庫的需求（單位/年）；FDj為配送中心的打開成本（元/年）；FPp為工廠的打開成本（元/年）；FSs為供應商的選擇成本（元/年）；ODj為配送中心訂貨成本（元/次）；OPp為工廠成品訂貨成本（元/次）；OMp為工廠原材料訂貨成本（元/次）；HDj為配送中心單位產品每年的庫存持有成本（元/單位）；HPp為工廠單位產品每年的庫存持有成本（元/單位）；HMp為工廠單位原材料每年的庫存持有成本（元/單位）；EDj為配送中心單位產品每年的梯級庫存持有成本（元/單位）；EPp為工廠單位產品每年的梯級庫存持有成本（元/單位）；EMp為工廠單位原材每年的料梯級庫存持有成本（元/單位）；MPp為工廠單位產品生產成本（元/單位）；MHp為工廠單位原材料處理成本（元/單位）；PHp為工廠單位成品處理成本（元/單位）；DHj為配送中心單位成品處理成本（元/單位）；PSs為供應商的單位原材料售價（元/單位）；TDji為從配送中心到顧客的單位運輸成本（元/單位）；TPpj為從工廠到配送中心的單位運輸成本（元/單位）；TSsp為從供應商到工廠的單位運輸成本（元/單位）；BOM為成品和原材料之間的數量關系；B為大的正數。

決策變量：XDj為如果配送中心打開取1，否則取0；XPp為如果工廠打開取1，否則取0；XSs為如果供應商被選用取1，否則取0；YDji為如果配送中心和顧客之間建立服務關系取1，否則取0；YPpj為如果工廠和配送中心之間建立服務關系取1，否則取0；YSsp為如果供應商和工廠之間建立服務關系取1，否則取0；QPpj為工廠到配送中心的運輸量（單位/年）；QSsp為供應商到工廠的運輸量（單位/年）；OQDj為配送中心訂貨批量（單位/次）；OQMp為工廠原材料訂貨批量（單位/次）；OQPp為工廠成品訂貨批量（單位/次）。

2.2 模型數學描述

整合供應商選擇的多層級LIP模型，以設施的打開成本、原材料和成品庫存成本、原材料采購和運輸成本、成品的生產和運輸成本之和最小為目標，同時對供應商的選擇、工廠和配送中心的選址、配送中心和顧客之間的分配關系、層級之間的運輸量以及工廠和配送中心的訂貨批量進行決策，模型如下：

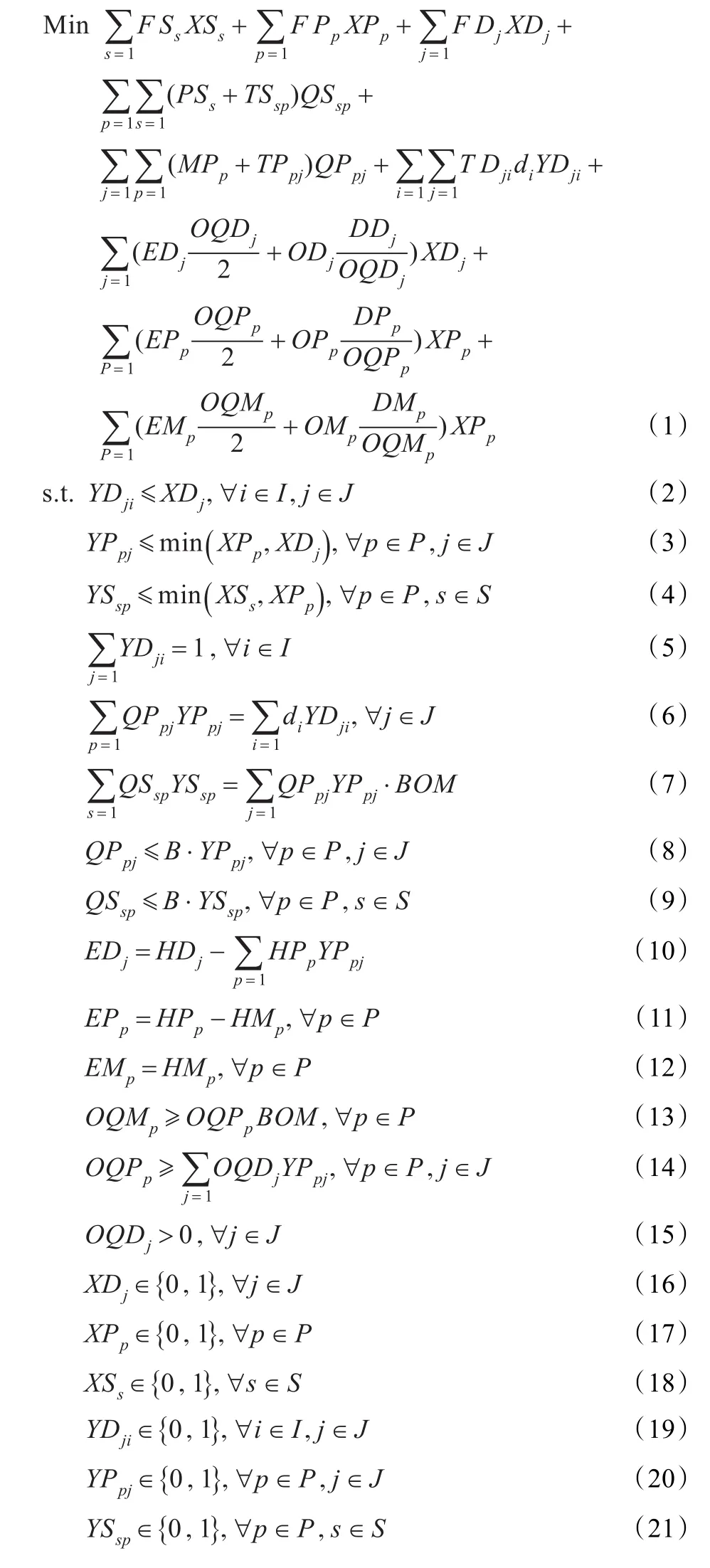
其中，式（1）是模型的目標函數，前三項分別是供應商的選擇成本、工廠和配送中心的打開成本；第四項是原材料的采購和運輸成本，第五項是產品的生產和從工廠到供應商的運輸成本；第六項是從配送中心到顧客的運輸成本；第七項是配送中心的庫存持有成本；第八和第九項是工廠的庫存持有成本。式（2）表示只有當配送中心打開后，才能為顧客提供服務；式（3）和（4）表示只有當供應商、工廠和配送中心都打開后，它們之間才能建立服務關系；式（5）表示一個配送中心就能完全滿足一個顧客的需求；式（6）和（7）分別是進出配送中心和工廠的產品數量相等；式（8）和（9）表示供應商、工廠和配送中心之間運輸量的取值限制；式（10）是配送中心的梯級庫存持有成本；式（11）和（12）分別是工廠成品和原材料的梯級庫存持有成本；式（13）和式（14）是廠和配送中心訂貨批量關系限制；式（15）～式（23）是決策變量的取值限制。

3 算法設計

所建立的四層級LIP模型屬于混合整數非線性規劃模型，同時也是典型的NP困難問題，傳統的精確算法難以在有限時間內求解較大規模的問題，常用啟發式算法獲得在可接受時間花費下的可行解[14]。啟發式算法總體上可以分為個體搜索算法和群體搜索算法。個體搜索算法從單個個體開始，逐步往最優解靠攏，如貪心算法、松弛算法等。群體搜索算法從解的集合開始，采用并行搜索機制，接近最優解，如遺傳算法、粒子群優化算法（Particle Swarm Optimization，PSO）等。實踐證明，采用并行機制的群體搜索算法在效率上優于個體搜索算法。相對于遺傳算法，粒子群優化算法沒有交叉和變異操作，只是通過內部速度進行更新，因此原理更簡單、參數更少、實現更容易。因此，PSO被廣泛應用于各個領域，是求解非線性連續優化、混合整數非線性優化、組合優化問題的有力工具[15]。所以，本文采用PSO算法求解所建立的模型。同時，為了對PSO算法的求解能力進行評價，將PSO算法的求解結果與基于分支定界算法的Lingo軟件求解結果進行比較。

3.1 粒子群初始化

粒子群初始化包括粒子的編碼和粒子群的生成。上述LIP模型的決策變量包含0-1整數變量和連續非負變量兩大類，經過試驗發現，由于模型過于復雜，無論是全部采用二進制編碼，還是采用混合編碼，都很難得到滿足所有約束條件的可行解。因此，本文采用部分編碼的策略，僅對其中的選址變量進行編碼（二進制編碼）。一旦選址變量確定后，運輸量通過求解最小成本網絡流問題得到。由于運輸量的有無反映了節點之間的網絡拓撲關系，因此不需要對其進行專門的編碼。訂貨批量通過求解EOQ模型得到，進而得到總的運輸成本和總的庫存成本。

在上述編碼規則下，每一個粒子的長度為候選供應商、工廠和配送中心數量之和，粒子群采用隨機的方法生成。

3.2 適應度函數的確定

在選址變量確定后，可以得到總的選址成本LocaC。通過求解如下的最小成本網絡流問題得到總的運輸成本TraficC。

模型中，QDj是配送中心到顧客的運輸量，其他變量含義同前。采用最小費用增廣路徑算法求解上述網絡流問題[16]，從而得到層級之間的運輸量和TraficC。在確定選址變量和運輸量的結果后，通過EOQ模型計算最初訂貨批量，再結合約束條件進行調整，進而得到滿足約束的訂貨批量和總的庫存成本InvetC。

通過上述分布求解的方式，有效地消除了所有的約束。因此，適應度函數為：

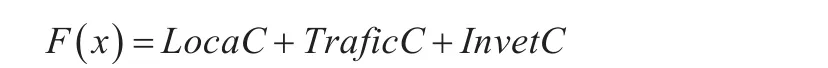
3.3 速度和位置的更新

適應度函數確定后，計算各個粒子的適應度值，并對個體極值和群體極值更新。然后，對粒子速度和位置進行更新。在離散空間下，速度和位置的更新公式如下[17]：

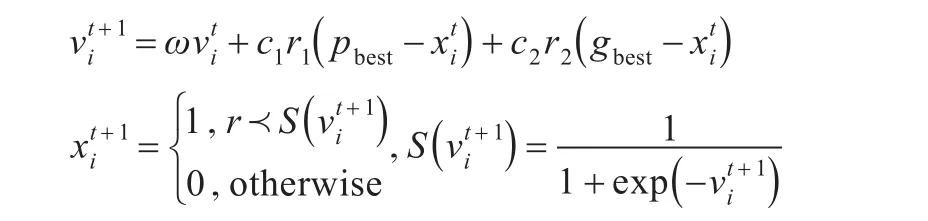
其中，ω稱作慣性權重，c1、c2為常數，稱作學習因子（也叫加速系數），r1、r2是兩個0到1之間的隨機數。

4 算例仿真

粒子群算法程序用Matlab 7.10中的M語言編寫，測試用的計算機處理器為Intel?CoreTMi5-2410 CPU，單核頻率為2.30 GHz，2.0 GB的內存，操作系統為Windows 7家庭普通版。為了對PSO進行評估，同時用優化求解軟件Lingo 9.0求解每一個算例。

4.1 算例數據

根據問題規模隨機生成20個算例，每一個算例有不同的節點數量，總的節點數量從50變化到170個。例如，算例“5-10-15-20”表示該算例中候選的供應商有5個，工廠有10個，配送中心有15個，顧客有20個。

各算例的數據產生規則如下：供應商的固定選擇成本，工廠和配送中心的打開成本和服從[5 000，15 000]之間的均勻分布；供應商到工廠的單位運輸成本服從[5，15]之間的均勻分布，工廠到配送中心的單位運輸成本服從[20，50]之間的均勻分布，配送中心到顧客的單位運輸成本服從[100，200]之間的均勻分布，供應商的原材料采購成本服從[200，300]之間的均勻分布，工廠的單位生產成本服從[1 000，1 500]之間的均勻分布；工廠成品一次訂貨成本服從[1 500，2 000]之間的均勻分布，工廠原材料一次訂貨成本服從[2 000，2 500]之間的均勻分布，工廠成品的單位庫存持有成本服從[150，200]之間的均勻分布，工廠單位原材料庫存持有成本服從[50，100]之間的均勻分布，配送中心一次訂貨成本服從[3 000，4 000]之間的均勻分布，配送中心的單位庫存持有成本服從[500，800]之間的均勻分布；顧客的需求服從[1 000，3 000]之間的均勻分布。對于所有的算例，BOM都取2。

另外，設定3 600 s的時間限制作為Lingo算法的終止條件，粒子群算法的終止條件為連續10次迭代，適應度函數沒有明顯的改進。

4.2 算法比較

上述20個算例分別用Lingo 9.0和PSO算法求解，結果如表1所示。第一列“測試算例”表明了每一個算例中候選供應商、工廠、配送中心和顧客的數量；第二列和第三列是Lingo 9.0求解后得到的結果，分別是目標函數最小值（“cost”單位是元）和運算所用時間（“T”單位是s）；第四列和第五列是PSO算法求解后的結果，同樣包含目標函數最小值和運算所用時間。從表1可以看出：有55%的算例lingo9.0不能在3 600 s內得到求解結果，尤其是當總節點數超過110個以后，全部都不能得到最小成本，而PSO算法對于所有的算例在較短時間內都能得到最小成本。這表明PSO的求解能力優于優化軟件。

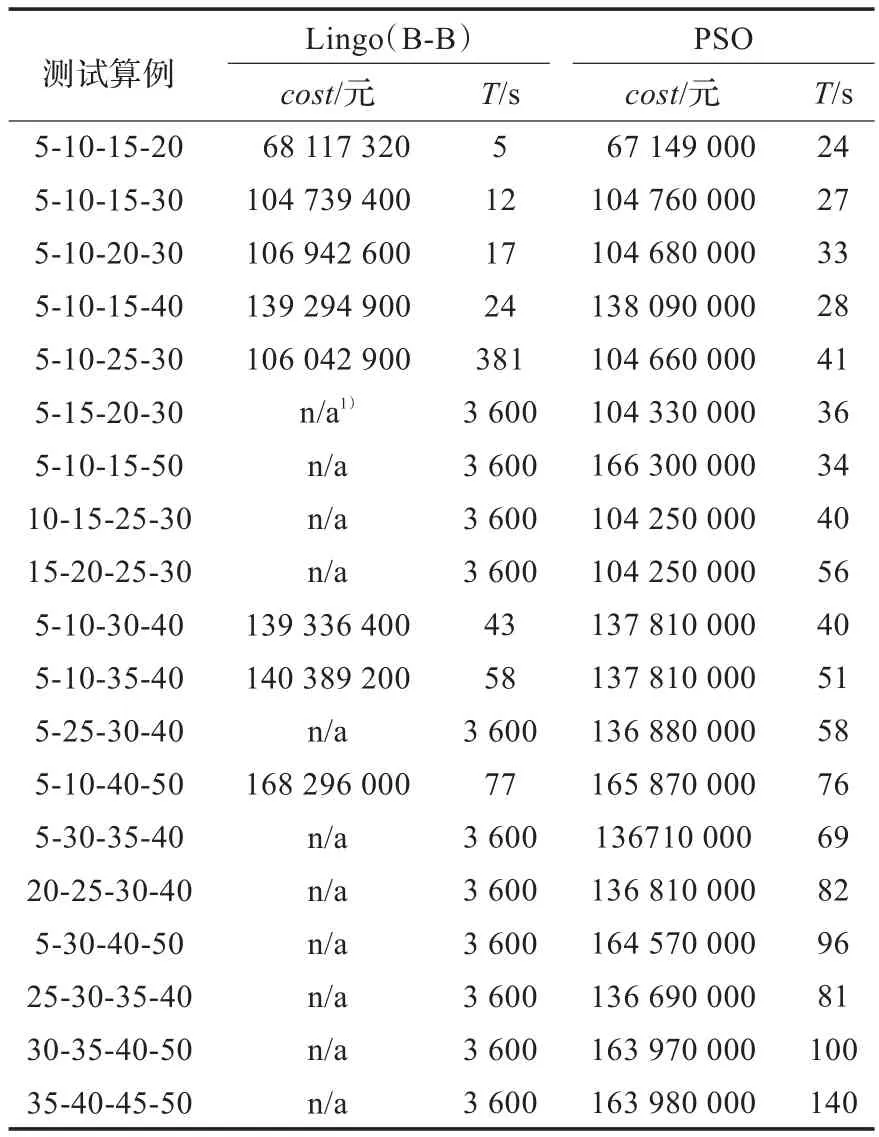
表1 算例求解結果

從兩種算法都能得到最小成本的算例來看（圖1），Lingo 9.0所得到的解都要大于PSO。這說明基于分支定界算法的Lingo 9.0在有限的時間內只能獲得局部最優解，而且這種局部最優解比PSO的解質量差。

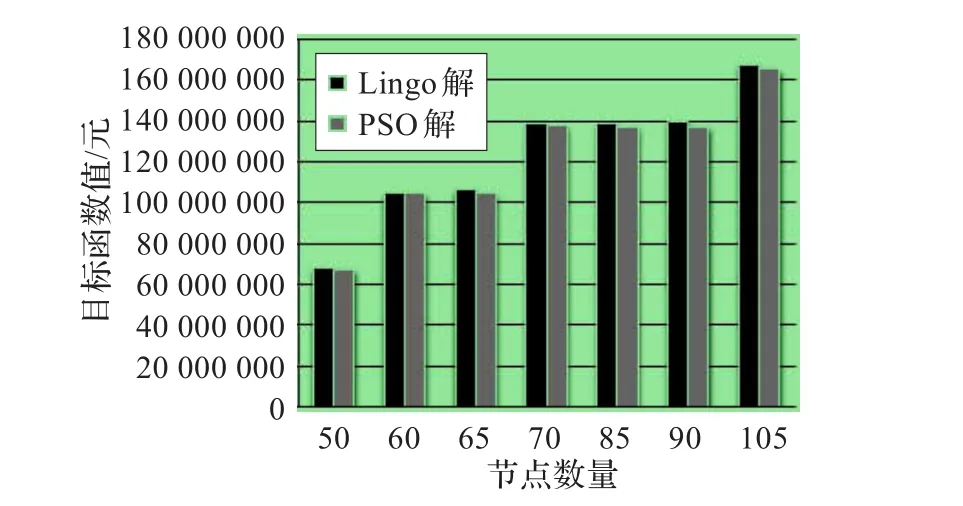
圖1 PSO和Lingo的求解結果比較

從兩種算法的求解時間來看（圖2），在節點數小于70個的時候，Lingo 9.0的獲得最小成本的時間要少于PSO；當節點數超過70個時，情況剛好相反。而且，隨著節點數的增加，Lingo 9.0的求解時間增加速度非常快，超過了PSO求解時間的增加速度。

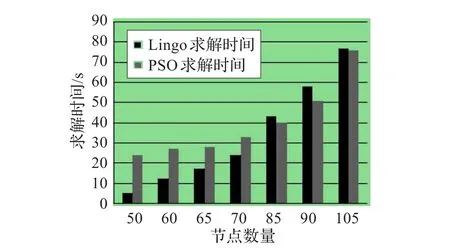
圖2 PSO和Lingo的求解時間比較

5 結論

供應鏈網絡設計是供應鏈管理的戰略決策問題，對供應鏈的績效有重要的影響。合理設計供應鏈網絡，要求建立選址和庫存的集成決策模型。本文針對由供應商、工廠、配送中心和顧客構成的供應鏈，考慮工廠和配送中心庫存決策的相互影響，運用梯級庫存的概念，建立了整合供應商選擇的多層級的LIP模型。針對模型的特點，設計了PSO算法；通過對20個算例的求解，可以看出本文所設計的PSO算法無論是在得到的最小總成本，還是運算速度上都明顯優于數學規劃求解軟件Lingo，尤其是當總節點數較大時。算例也表明，本文所建立的模型是有效的，設計的算法是可行的，可以用于多層級的一體化供應鏈網絡設計。在未來的研究中，可以考慮需求的不確定性和更為復雜的多級庫存控制模型。

[1]Mccann P.The logistics cost location-production problem[J]. Journal of Regional Science，1993，33（4）：503-516.

[2]Baumol W J，Wolfe P.A warehouse-location problem[J].Operations Research，1958，6（2）：252-263.

[3]Nozick L K，Turnquist M A.Integrating inventory impacts into a fixed-charge model for locating distribution centers[J]. Transportation Research Part E，1998，34（3）：173-186.

[4]Shen Z J M.Efficient algorithms for various supply chain problems[D].Evanston，IL：Northwestern University，2000.

[5]Axsater S.Using the deterministic EOQ formula in stochastic inventory control[J].Management Science，1996，42（6）：830-834.

[6]Snyder L V，Daskin M S，Teo C P.The stochastic location model with risk pooling[J].European Journal of Operational Research，2007，3（179）：1221-1238.

[7]Miranda P A，Garrido R A.Incorporating inventory control decisions into a strategic distribution network design model with stochastic demand[J].Transportation Research Part E，2004，40：183-207.

[8]Park S，Lee T T，Sung C S.A three-level supply chain network design modelwith risk-pooling and lead times[J]. Transportation Research Part E，2010，46：563-581.

[9]Berman O，Krass D，Tajbakhsh M M.A coordinated locationinventory model[J].European Journal of Operational Research，2012，217：500-508.

[10]譚凌，高峻峻，王迎軍.基于庫存成本優化的配送中心選址問題研究[J].系統工程學報，2004，19（l）：59-66.

[11]Romeijn H E，Shu J，Teo C P.Designing two-echelon supply networks[J].European Journal of Operational Research，2007，178：449-462.

[12]Roundy R O.98%effective integer-ratio lot-sizing for one warehouse multi-retailer systems[J].ManagementScience，1985，31：1416-1430.

[13]Tancrez J S，Lange J C，Semal P.A location-inventory model for large three-level supply chains[J].Transportation Research Part E，2012，48：485-502.

[14]邢文訓，謝金星.現代優化計算方法[M].北京：清華大學出版社，2003：13-23.

[15]楊維，李歧強.粒子群優化算法綜述[J].中國工程科學，2004，6（5）：87-94.

[16]Ahuja R，Magnanti T，Orlin J.Network flows：theory，algorithms，and applications[M].New York：Prentice Hall，1993.

[17]Kennedy J，Eberhart R C.Discrete binary version of the particle swarm algorithms[C]//Proceedings of the IEEE InternationalConferenceon Systems，Man，Cybernetics. Orlando：IEEE Press，1997：4104-4108.

SHUI Wenbing,HE Baohong,HE Min

Faculty of Transportation Engineering,Kunming University of Science&Technology,Kunming 650500,China

To deal with the integrated decisions of location and inventory for the supply chain network design with multi-echelons, a new location-inventory model based on echelon stock policy is developed in which the selection of suppliers is considered. The objective of the model is to determine the number and locations of suppliers,plants and Distribution Centers（DCs）,the assignment of each customer to a DC,the transportation quantity between suppliers,plants and distribution centers,and the optimal order quantity in the opening plants and DCs,which minimizes the system-wide location,production,purchase,transportation,and inventory costs.The particle swarm optimization algorithm based on partial encoding is designed to solve the proposed model.The results of 20 numerical examples of different scale show that the model is effective and can be used to design some four echelons supply chain network,and the PSO algorithm designed performs better than mathematic optimization software of Lingo 9.0 whatever the precision or the speed,especially when there are many nodes in the supply chain.

location-inventory model;selection of suppliers;particle swarm optimization algorithm;partial encoding

針對多級供應鏈網絡設計中選址和庫存一體化決策問題，基于梯級庫存策略，建立了整合供應商選擇的多層級選址-庫存模型。模型以網絡中供應商的選擇成本、工廠和配送中心的打開成本、層級之間的運輸成本、庫存成本、采購成本和生產成本之和最小為目標，同時對供應商的選擇、工廠和配送中心的選址、配送中心對顧客的分配、層級之間的運輸量、工廠和配送中心的訂貨批量進行決策。為了求解所建立的模型，設計了基于部分編碼的粒子群優化算法。20個不同規模的算例測試表明：所建立的模型是有效的，能用于多層級供應鏈網絡的設計；所設計的算法無論是在求解精度，還是在運算速度上都明顯優于數學優化軟件Lingo 9.0，尤其是當供應鏈網絡中總節點數較大時。

選址-庫存模型；供應商選擇；粒子群優化算法；部分編碼

A

F252

10.3778/j.issn.1002-8331.1305-0245

SHUI Wenbing,HE Baohong,HE Min.Multi-echelons location-inventory model with selection of suppliers.Computer Engineering and Applications,2013,49（23）：1-5.

國家自然科學基金項目（No.51068013）；云南省科技廳應用基礎研究計劃項目（No.2011FZ054）。

稅文兵（1982—），男，博士，講師，研究領域為物流系統設計與優化；何保紅（1973—），女，博士，副教授，研究領域為交通運輸規劃與管理；何民（1972—），男，博士，教授，研究領域為交通運輸規劃與管理。E-mail:swbzzq@126.com

2013-05-20

2013-07-18

1002-8331（2013）23-0001-05

CNKI出版日期：2013-07-29 http://www.cnki.net/kcms/detail/11.2127.TP.20130729.1105.005.html