基于階比復雜度的滾動軸承早期故障診斷

黃炯龍，呂建新，馬文龍，曹紅燕

(1.武警工程大學，西安 710086；2.廣西師范大學，廣西 桂林 541004)

滾動軸承作為各種工程機械設備中的關鍵組成部件，其工作狀況對整個機組的正常運行有著重要的影響。軸承的故障診斷主要包括2個步驟:(1)從原始的軸承振動信號中提取某些特征；(2)利用人工智能方法對所提取的特征進行判斷，以確定軸承是否存在故障[1]。

上述針對軸承早期的故障診斷主要是對振動信號的波形參數進行特征提取，雖然具有一定的效果，但仍然存在以下不足：(1)與正常波形相比，軸承早期故障振動變化信息不明顯,簡單地通過波形參數并不能完全將軸承的早期故障信息表示出來；(2)不同狀態下的軸承故障信號由于能量量級差別明顯，可比性比較差；(3)噪聲對波形參數影響較為明顯，從而影響故障信息識別；(4)目前所使用的人工智能方法都需要故障樣本進行診斷，但軸承的早期故障樣本特征并不明顯，影響診斷的準確性和快速性。

軸承的早期故障信息往往會使該系統的動力學參數產生較為明顯的變化，因此，復雜度作為非線性時間序列分析中一個重要指標，對系統的狀態變化很敏感，可以作為軸承早期故障診斷的依據。由于軸的轉速不是恒定的，轉速上的波動會影響軸承振動信號的隨機性，從而影響復雜度的計算。階比跟蹤技術是針對轉頻不穩定機械的一種專用振動測量技術，它通過對軸轉速進行跟蹤實現恒角度增量采樣[2]，可將機械變速過程中產生的與轉速有關的振動信號有效地分離出來，同時對與轉速無關的信號起到一定的抑制作用[3]。由于階比跟蹤按轉角位置重新分配信號的采樣間隔，所以剔除了轉速變化對信號隨機性的影響。

1 復雜度

文獻[4]將復雜度定義為產生某給定“0，1”序列所必需的最少的計算機程序的比特數。文獻[5]在上述定義下提出了一種基于系統內在結構或過程的量度符號序列復雜性的簡單算法，即L-Z復雜度。

(1)已知重構序列{x1,x2,…,xn}，令

(1)

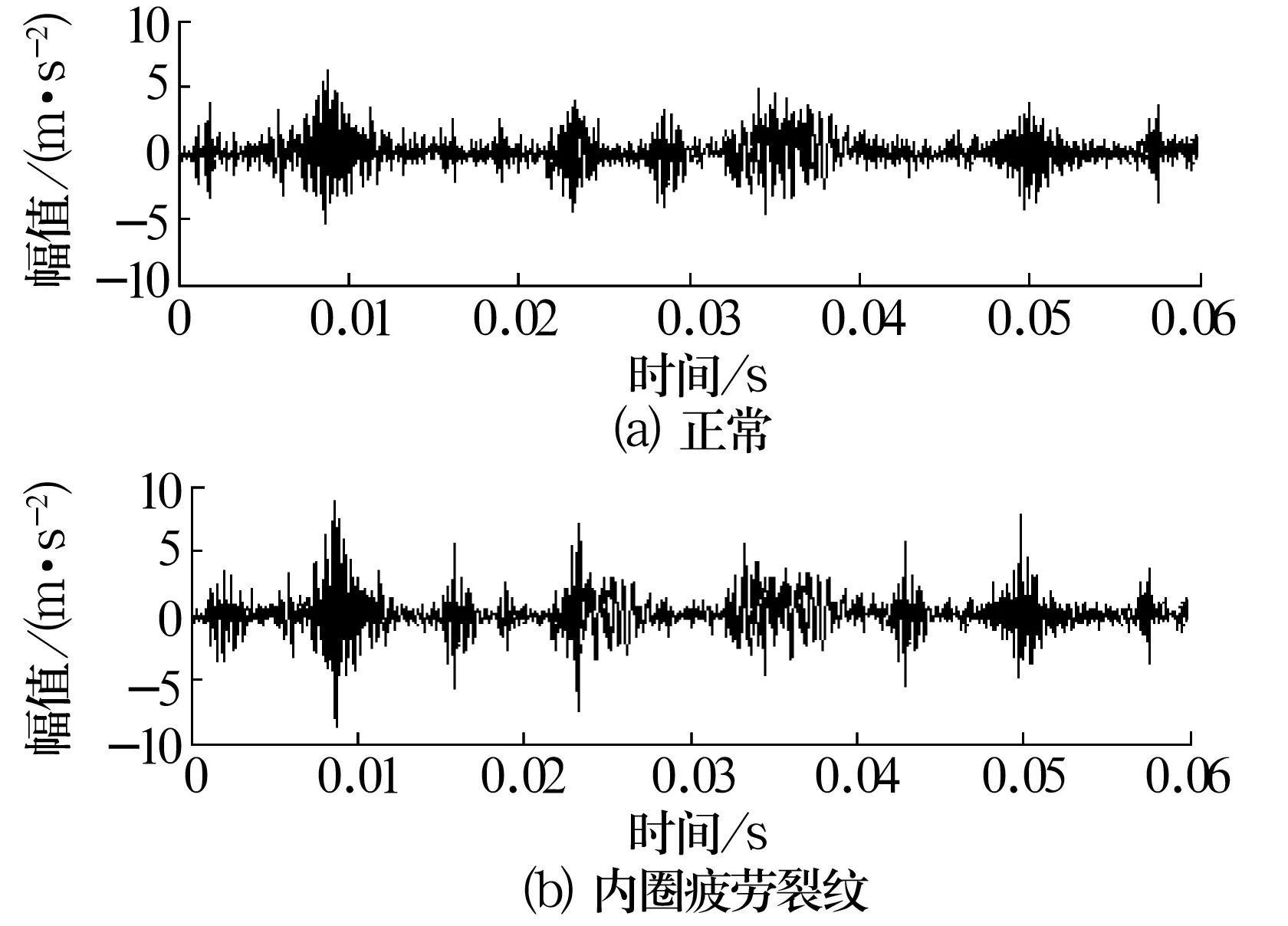
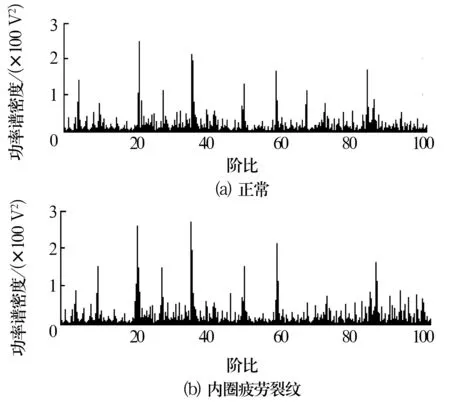
(2)根據(1)式將{x1,x2,…,xn}映射為新的序列{s1,s2,…,sn}，令Q=sr+1，r

(3)將“?”前的所有字符看作S，重復上述步驟直至生成整個序列。

(4)根據上述步驟得到一個用“?”分段的字符串，該字符串被“?”分成段的數目即為該序列的復雜度C(n)。

(5)據文獻[5]的研究，幾乎所有0，1隨機序列的復雜度都趨于值B(n)，即

(2)

通過歸一化，可得相對復雜度

R(n)=C(n)/B(n)。

(3)

由上述算法可知，復雜度反映了隨序列長度增長而產生新模式的速度，相對復雜度R(n)反映一個序列與隨機序列的接近程度，即序列復雜度越大，說明數據在某一時期內的新變化越多，發生新變化的速率越快，表明數據變化是無序而復雜的。反之，如果復雜度越小，則說明該序列發生新變化的速率越慢，周期性越強，數據變化是規律的。當信號完全為隨機信號時，R(n)=1；當信號為周期信號時，R(n)=0。

綜上所述，復雜度能夠描述序列發生變化的情況，可以作為振動信號所代表的軸承系統狀態的非線性特征參數。

2 基于階比復雜度的軸承故障診斷

由于軸承周圍噪聲信號的相對復雜度接近1，會直接影響軸承振動信號的復雜度，對故障特征提取不利。故選用小波閾值法先對信號降噪以減小噪聲信號的影響。

基于階比復雜度的軸承故障診斷具體包括以下步驟：

(1)選取db4小波對信號進行小波閾值降噪；

(2)根據文獻[6]，軸承的參考軸在短時間內可看作是勻變速運動，因此，參考軸轉角-時間函數可用多項式表示為

θ(t)=b0+b1t+b2t2+···+bntn，

(4)

式中：bn為待定系數，可以通過角域重采樣后的數據獲得；t為時間點。

在時域信號中，轉過相等角度Δα的連續時間為ti，可得

(5)

將(5)式代入(4)式，可求得待定系數bn，為簡化計算取n=3得

(6)

(7)

將t0，t1，t2和對應的參考軸轉角代入(4)式可得

(8)

由此可以得出關于等角度采樣點的方程，在求出信號對應的時間點后通過插值算法即可實現時域信號的計算階比跟蹤重采樣，得到等角度分布的采樣點χ(m)；

(3)按前面所述步驟計算角域信號χ(m)的相對復雜度Ri(n)，通過不同的相對復雜度Ri(n)判別軸承的早期故障。

3 試驗與分析

在某型齒輪箱振動試驗臺上進行試驗驗證，試驗系統中由電動機帶動輸入軸,輸出軸帶動負載，主動齒輪齒數Z1=35，被動齒輪齒數Z2=50。軸承疲勞裂紋是軸承早期故障的主要形式，因此試驗選取正常和模擬內、外圈疲勞裂紋的6206Z軸承樣本進行分析。軸承內徑30 mm，外徑62 mm，寬度16 mm，極限轉速為11 000 r/min，分別在內、外圈上通過線切割制作深1 mm，寬1 mm的溝槽模擬軸承早期疲勞裂紋故障。

鑒于加速階段的振動信號與恒轉速時相比往往含有更多的軸承故障信息，為了能在信號中進一步突出軸承的早期故障，在軸轉速由靜止加速至1 500 r/min的過程中對軸承信號進行等時間的同步采樣，采樣頻率為12 kHz，采樣時間為2 s。

無故障狀態和模擬內圈疲勞裂紋的軸承振動信號時域波形如圖1所示，從圖中可以看出，正常狀態與早期故障軸承時域波形沒有明顯差別。

圖1 軸承時域信號

為了進一步對比傳統階比分析與階比復雜度的故障識別效果，首先，采用傳統階比分析方法，在對時域信號進行角域重采樣后進行FFT分析，結果如圖2所示。從階比圖中可以看出，軸承的早期故障無法得到有效的識別。然后，采用階比復雜度對10組經過角域重采樣后的信號進行分析，計算所得復雜度見表1。

圖2 軸承階比譜

根據相關數據分析，該型號軸承正常工況下復雜度一般為0.3～0.4，復雜度大于0.5即可認為該軸承可能出現了早期故障。從表中可以看出，軸承內、外圈疲勞裂紋信號的復雜度明顯大于正常狀態下的軸承振動信號，說明軸承早期故障會使振動信號表現出更強的隨機性。受振動信號傳遞路徑的影響，軸承的內、外圈裂紋也表現出不同的復雜性測度，且外圈裂紋對應信號的復雜度大于內圈。由此可以根據軸承信號的相對復雜度來判別軸承的早期疲勞裂紋故障。

表1 軸承振動信號相對復雜度對比

4 結束語

通過小波降噪和計算階比跟蹤不僅有效消除了轉速的波動對軸承振動信號復雜度計算的影響，還將時變時域信號轉變為準平穩角域信號，提高了復雜度計算的準確度。試驗結果表明：軸承的早期裂紋故障信息在時域和階比譜上不夠明顯，但與正常軸承相比，出現早期疲勞裂紋故障后，軸承振動信號的復雜度則會明顯增大。由此表明，與傳統的特征頻率分析相比，階比復雜度在表征軸承早期故障信息方面具有很強的能力，可作為軸承狀態監測和早期故障診斷的一種無量綱指標，無需經過其他復雜的模式識別方法即可實現軸承的早期故障診斷，與使用人工智能算法相比速度明顯提高。