基于PSO算法角接觸球軸承動態接觸角的求解
王連寶,胡小秋,芮紅鋒
(南京理工大學 機械工程學院,南京 210094)
高檔數控機床的進給系統必須具有良好的動態特性[1]。角接觸球軸承是進給系統普遍使用的支承軸承,其動態特性直接影響進給系統的整體性能。如今,角接觸球軸承的動態特性分析理論已經比較完善,主要的難點集中在軸承動態模型的求解方面,目前多選用Newton-Raphson法、Hook-Jeeve法和差分法等[2-4]。上述方法對迭代初值敏感,求解不易收斂[5]。與之相比,二次插值型粒子群優化(Particle Swarm Optimization, PSO)算法對邊界初值的設定沒有嚴格的要求,具有很好的全局尋優能力。
1 軸承動態特性分析的簡化模型
1.1 幾何相容方程
對于內圈轉動、外圈固定的角接觸球軸承,受到聯合載荷(軸向力Fa和徑向力Fr)作用前后位于角位置ψj處的球心與內、外溝曲率中心的相對位置關系如圖1所示。根據圖1的變形幾何條件得
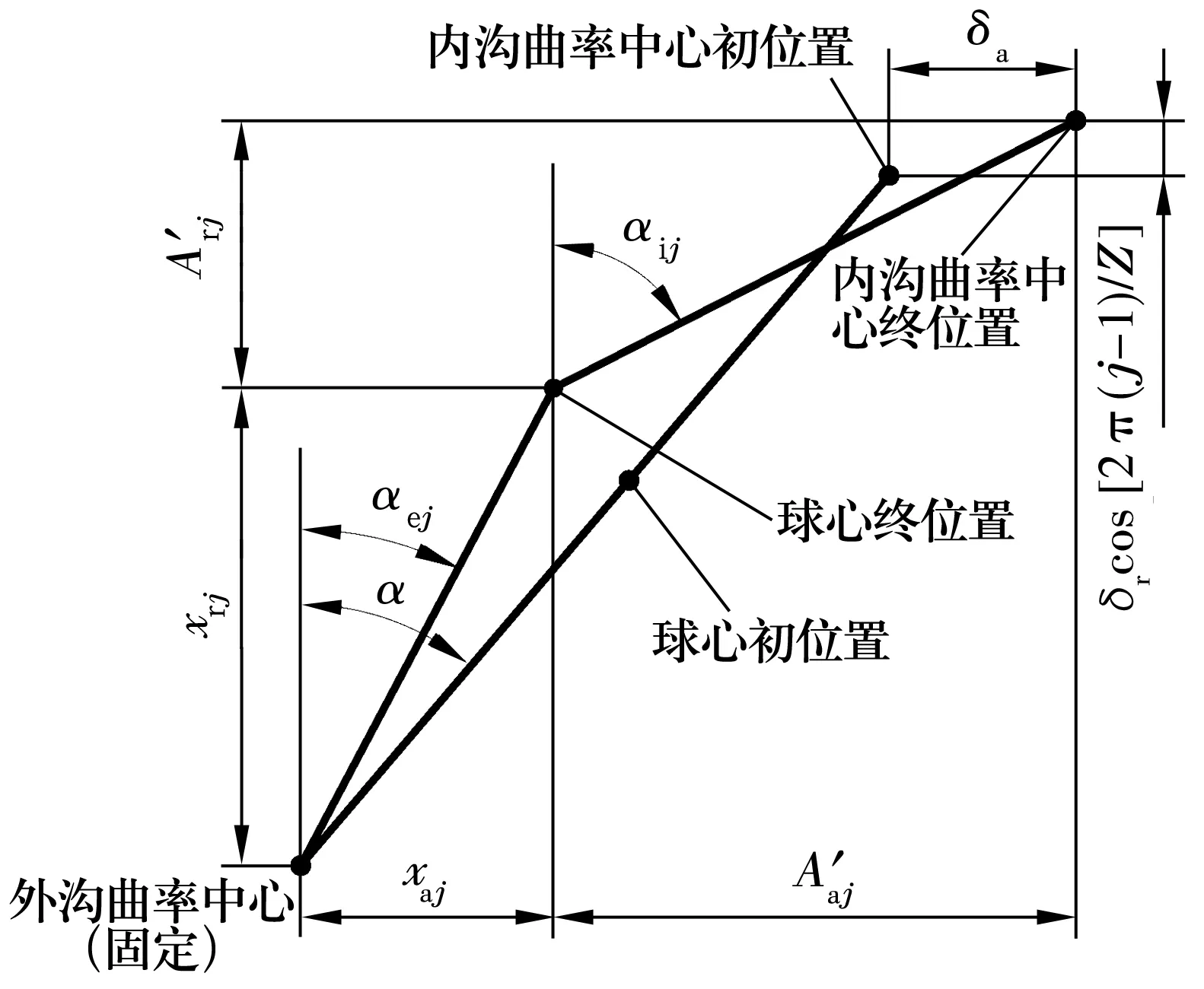
圖1 球心與內、外溝曲率中心的位置關系
(1)
(2)
式中:fi,fe分別為內、外溝曲率系數;δij,δej分別為內、外溝道的法向接觸變形量;Dw為球直徑;Kij,Kej分別為內、外溝道的接觸剛度;Qij,Qej分別為內、外溝道的法向接觸載荷;xaj,xrj,A′aj,A′rj為與球心和內、外溝曲率中心坐標相關的變量;j=1,2,…,Z;Z為球數。
1.2 內圈力平衡方程
在Fa和Fr作用下,軸承處于受力平衡狀態,對內圈有
(3)
(4)
式中:αij,αej分別為內、外接觸角。
1.3 動態模型簡化前、后的比較
文獻[2,5-6]中的動態模型包含一系列輔助方程和4Z+2個主方程,主變量較多且彼此耦合,增加了算法的復雜性,也降低了計算精度,需要對動態模型的主方程組進行簡化并尋找新的算法。
與以往的動態模型相比,簡化模型中增加了2Z個輔助方程,主方程數目減為2Z+2個,縮減了主變量個數,簡化了適應度函數Fitness。
2 求解方法及流程
簡化模型中變量Kij,Kej,Qij,Qej,δij,δej,xrj,xaj,A′rj和A′aj最終都是關于αij與αej的函數,其邏輯關系如圖2所示。
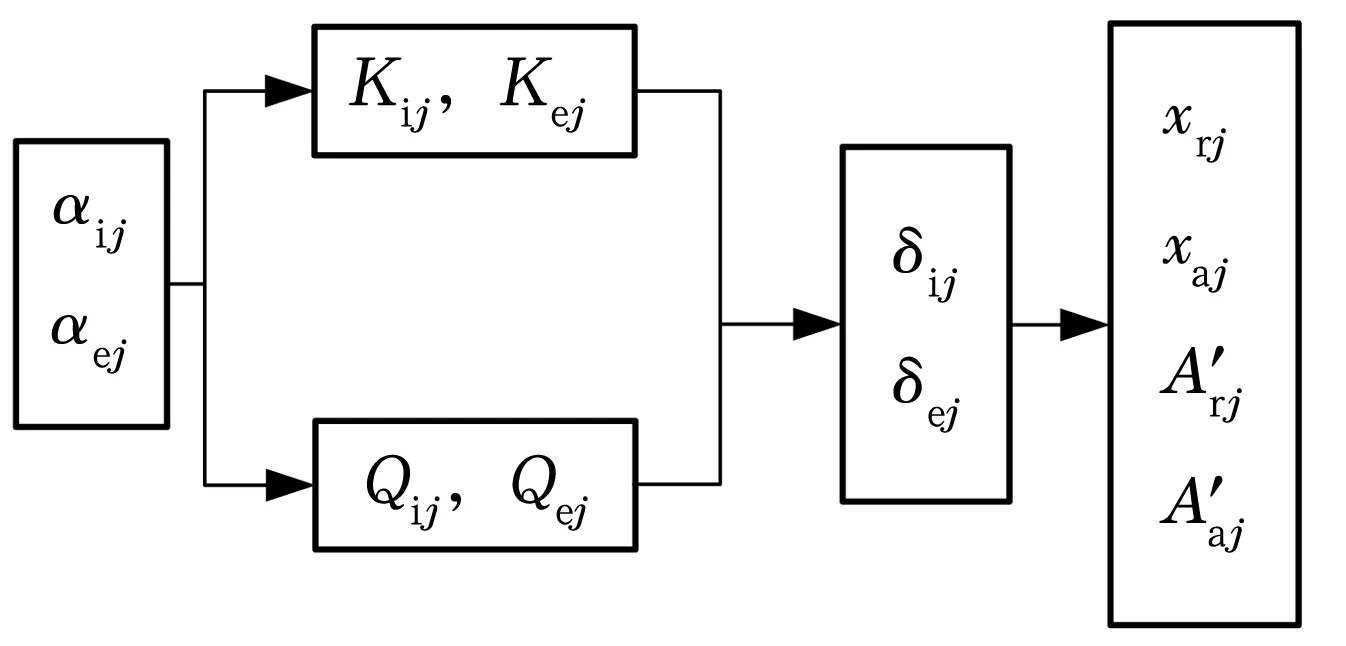
圖2 變量之間的邏輯關系
取一組接觸角αij與αej為粒子元素,適應度函數Fitness由 (1) ~ (4) 式左邊表達式組成,即
|Expr3|+|Expr4|,
當軸承轉速不為零時,每個球受到離心力和陀螺力矩的作用,接觸角按一定規律變化。研究表明,在一定的外加載荷作用下,隨著轉速的升高,內接觸角逐漸增大,外接觸角逐漸減小,且內接觸角大于外接觸角。所以,在算法中設定約束條件為αej<αij。仿真表明:根據變量的實際意義確定未知量的約束條件,既提高了計算精度,又縮短了收斂時間。
PSO算法具有求解優化問題的能力,但在處理復雜、多維變量多峰值的數學模型時仍然存在“早熟收斂”現象[6],使得計算精度較低。為了改善這一問題,文中采用二次插值型PSO算法,該算法引入了基于二次插值的“早熟判斷和處理”機制,算法在出現粒子早熟時會跳出局部最優,所以具有很好的全局優化和局部探索能力。角接觸球軸承簡化模型動態接觸角的計算流程如圖3所示。
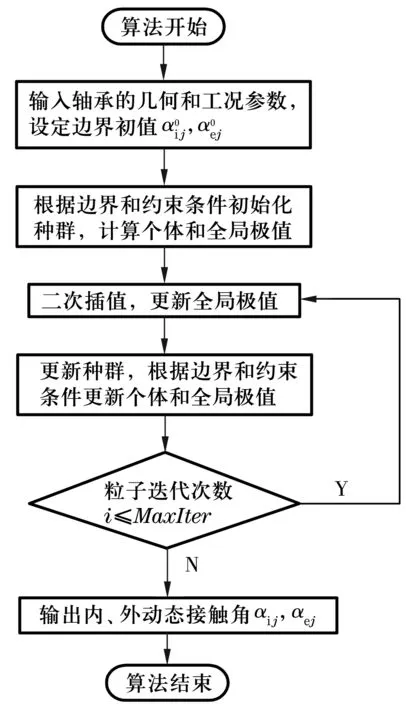
圖3 動態接觸角的計算流程
3 計算結果與分析
為了驗證簡化模型的正確性和二次插值PSO算法程序的可行性與普適性,選擇常規軸承SKF B218和高精密軸承SNFA VEX 6/NS為例,同時為了與已知文獻[7-8]對比,下面僅計算軸承在不同軸向力和轉速下的動態接觸角。
3.1 SKF B218的分析
SKF B218的內、外圈與鋼球材料均為GCr15鋼,主要參數見表1。

表1 SKF B218主要參數
3.1.1 動態簡化模型和算法的驗證
當軸向力Fa=17.8 kN,轉速n取不同數值時,內、外接觸角的計算值與文獻值[7-8]見表2。由表2可以看出,低速時內、外接觸角的計算結果與文獻值之間的相對誤差很小,在±0.21%以內;隨著轉速的升高,計算誤差略微增大,但仍然較低,基本上在±1.09%以內。這是因為在軸承轉速較低時,實際內、外接觸角的差值較小,程序可以設定較小范圍(上、下邊界初值的差較小)的接觸角邊界初值;而高速時,實際內、外接觸角的差值增大,需要設定較大范圍的邊界初值,致使計算誤差也偏大。
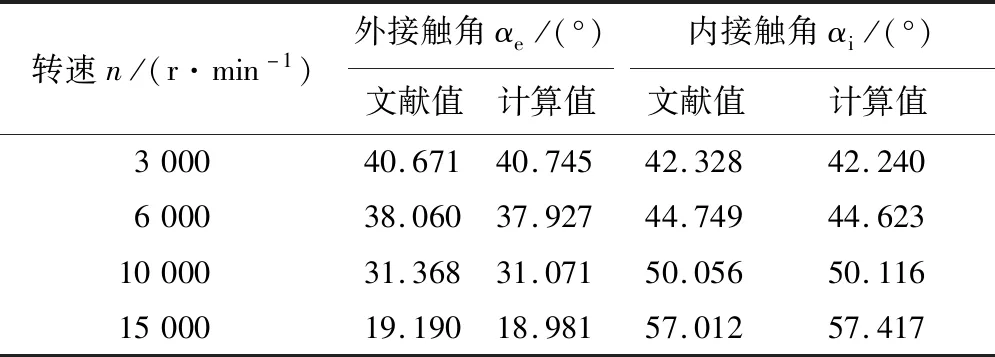
表2 計算值與文獻值的對比結果
圖4給出了軸承轉速n=15 000 r/min,軸向力Fa取不同值時內、外接觸角的文獻值與計算值變化曲線。由圖4可知,內、外接觸角的計算值分別與對應的文獻值變化趨勢相一致;當軸向力較小時,內、外接觸角的計算誤差相對較大,達到±2.56%;隨著軸向力的增大,計算誤差減小,低至±0.31%。這是因為隨著軸向力的增大,內接觸角逐漸減小,外接觸角逐漸增大,兩者之間的差值呈現遞減的變化趨勢,所以當軸向力較大時可以設定較小范圍的邊界初值,降低計算誤差。
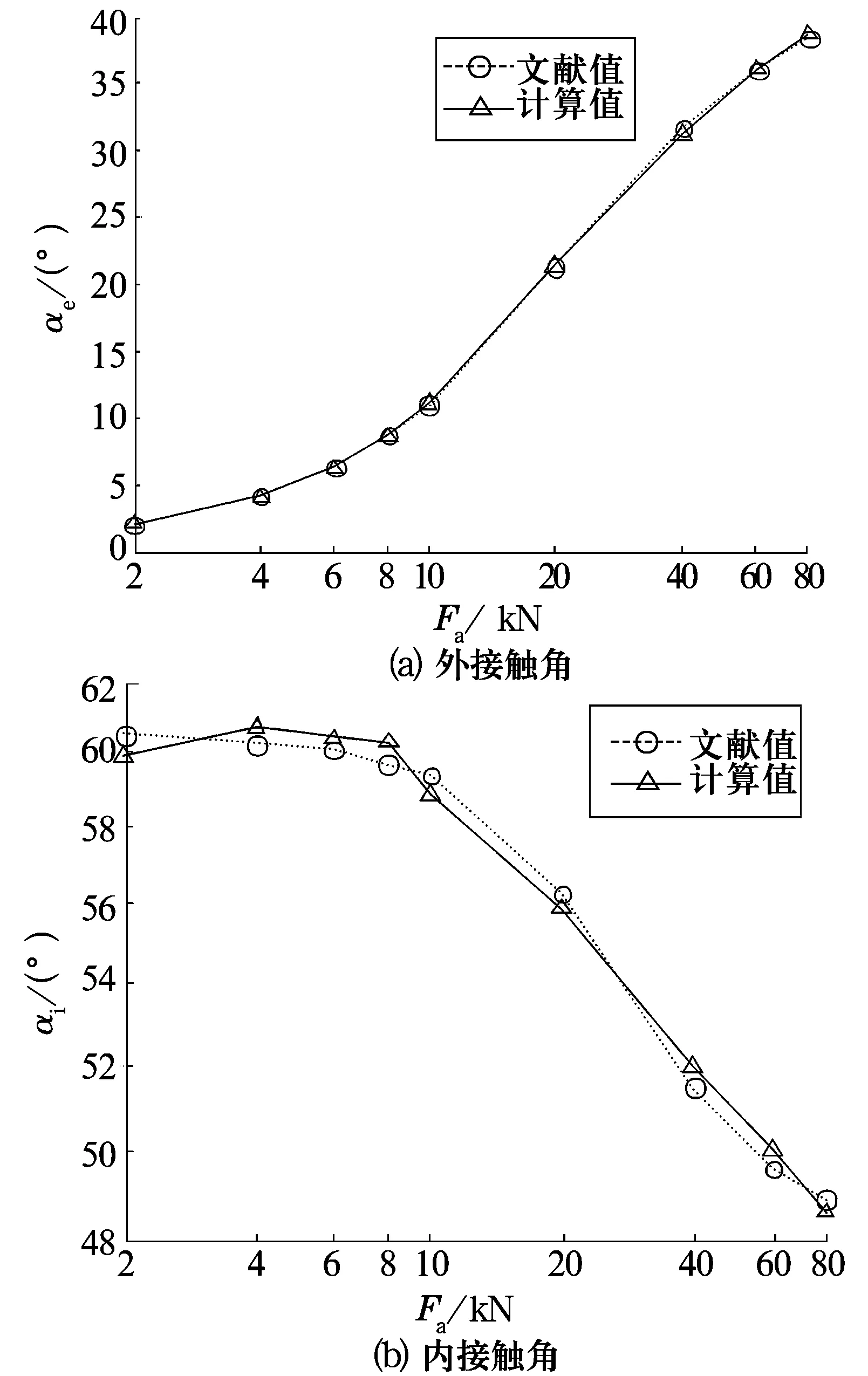
圖4 軸承動態接觸角隨軸向力的變化曲線
3.1.2 邊界初值對計算結果的影響
軸承所受軸向力Fa=10 kN,轉速n=5 000 r/min工況下,內、外接觸角分別選定不同的邊界初值時的計算結果見表3。由表3可以看出,隨著邊界初值設定范圍的擴大,內、外接觸角的計算結果沒有一定的變化趨勢,這是由于PSO算法中初始化種群具有隨機性;并且,計算結果分別在[42.38°,43.45°],[38.90°,40.13°]內微幅震蕩,說明了此算法和程序具有很好的穩定性,邊界初值對計算結果影響很小。
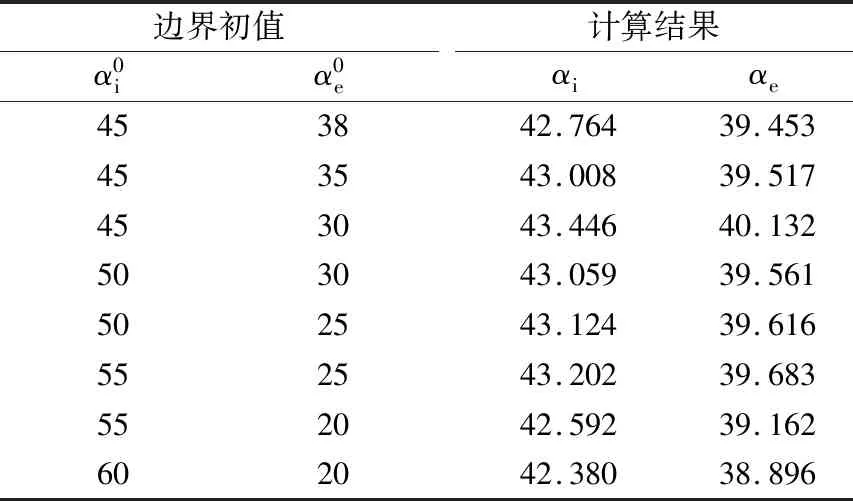
表3 不同初值下的計算結果(SKF B218) (°)
3.2 SNFA VEX 6/NS的分析
SNFA VEX 6/NS是一種高精密的高速混合陶瓷球軸承,尺寸較小,其套圈材料為GCr15鋼,陶瓷球材料為Si3N4,主要參數見表4。

表4 SNFA VEX 6/NS的主要參數
當軸承轉速n=1.0×105r/min,軸向力Fa取不同數值時的文獻值[8]和計算值曲線如圖5所示。由圖5可知,內、外接觸角的計算誤差均在±4.31%以內,說明此算法對高精密軸承同樣具有較高的計算精度。
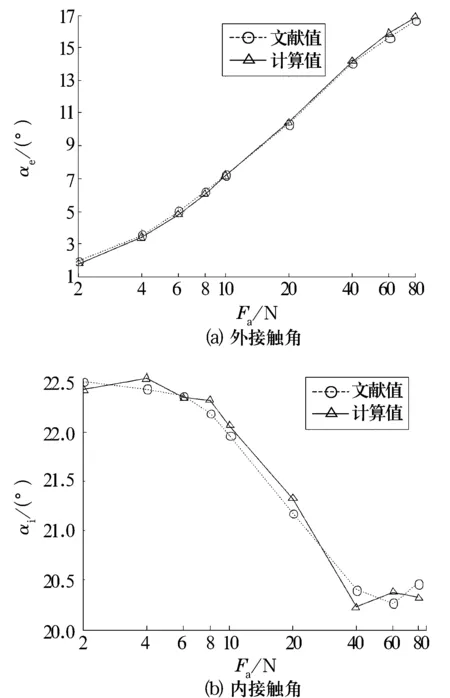
圖5 軸承動態接觸角隨軸向力的變化曲線
軸承在軸向力Fa=50 N,轉速n=1.0×105r/min工況下,內、外接觸角分別選定不同的邊界初值時的計算結果見表5。
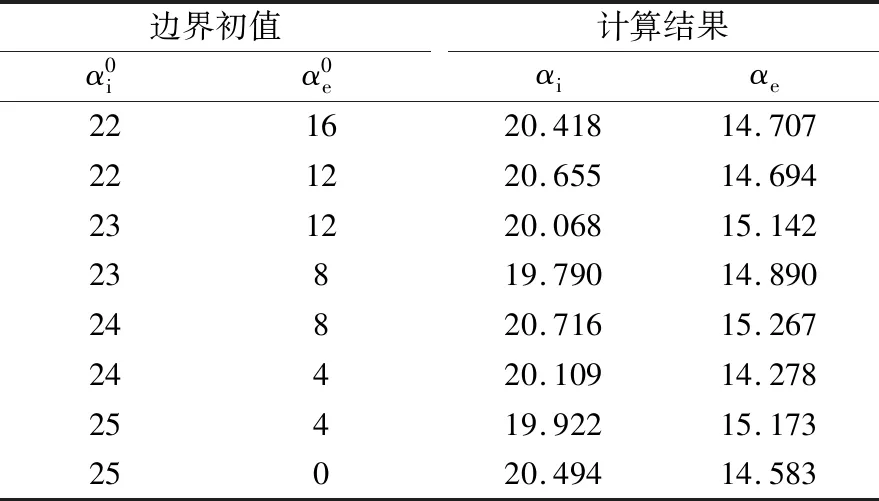
表5 不同初值下的計算結果(SNFA VEX 6/NS) (°)
由表5可以看出,內、外接觸角的計算結果分別在[19.79°,20.72°],[14.28°,15.27°]內小幅波動,說明了設定較大范圍的邊界初值對高精密軸承的計算結果影響不大,即上文算法適用于高精密軸承。
4 結論
(1)當軸向力一定時,隨著轉速的增大,內、外接觸角的計算誤差呈現遞增的變化趨勢;當轉速一定時,隨著軸向力的增大,計算誤差呈現遞減的變化趨勢。
(2)在軸向力、轉速變動范圍較大時,內、外接觸角的計算誤差小,說明提出的角接觸球軸承動態簡化模型具有較高的正確性,應用二次插值型PSO算法進行求解具有很好的可行性與普適性。
(3)當軸向力、轉速一定時,內、外接觸角設定不同的邊界初值范圍,其計算結果均在較小區間內變動,說明該算法對動態簡化模型的邊界初值敏感性較低,具有很好的穩定性,適用于計算常規軸承和高精密軸承。

