模糊數的梯形逼近

陸漢川，李生剛

陜西師范大學數學與信息科學學院，西安 710062

模糊數的梯形逼近

陸漢川，李生剛

陜西師范大學數學與信息科學學院，西安 710062

1965年，為了從數學上處理帶有模糊性的不確定現象，Zadeh[1]引入了模糊集合的概念。迄今為止，關于模糊集理論和應用的科學研究已有成千上萬，從中可以看出模糊集理論能讓人們更有效地處理不精確的信息。模糊數在其中扮演了一個重要的角色，因為不確定性和不完整的信息經常可以用模糊數（包括區間數）來表示。一個有趣的問題是怎樣利用一個梯形的或三角的模糊數去逼近一般的模糊數，這方面的研究引起了許多學者的興趣和關注[2-13]。在文獻[2]提出了推廣的梯形模糊數并給出了保持期望不變的梯形逼近的計算公式。本文在文獻[2]的基礎上推廣了梯形模糊數的一些性質，得到了更具體、更直觀的計算梯形逼近方法。此外，文中討論的模糊數逼近都是具有保持期望區間不變性的。

1 預備知識

下面是本文涉及到的一些定義。

類似于經典的算術，可以對模糊數進行加、減、乘、除運算。然而，由于模糊數的邊不是很規則，導致了這些運算將變得很復雜。所以，更希望在實際中能夠利用具有線性的或分段線性邊的模糊數，因為這些模糊數的隸屬函數是很簡單的，同時還有著更多合理的闡述。經常使用的模糊數是梯形模糊數，它們的兩邊是線性的且隸屬函數，有著下面的形式：

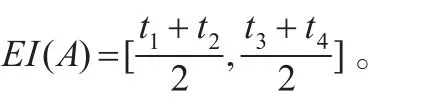
定義1.2[6]一個推廣的梯形模糊數A=[AL(α)，AU(α)]是一個次數小于或等于1（即degAL(α)≤1，degAU(α)≤1）的多項式函數有序對，記為Te(A)=(te1，te2，te3，te4)。A是一個推廣的三角形的模糊數當且僅當AL(1)=AU(1)，記為Ts(A)= (ts1，ts2，ts3，ts4)。兩個推廣的梯形模糊數A=[AL(α)，AU(α)]，B=[BL(α)，BU(α)]之間的距離d(A，B)類似于（1）定義。

定義1.3[6]一個模糊數A的推廣的梯形逼近Te=[t1+(t2-t1)α，t4-(t4-t3)α]定義為最小距離d(A，B)的推廣的梯形模糊數，這里B是一個推廣的梯形模糊數且保持期望區間不變。

眾所周知，一個模糊數A的推廣的梯形逼近Te(A)可能導致的不是一個模糊數[7-8]。最近的梯形逼近記為Tn(A)，它被看做保持一個模糊數A的期望區間EI(Tn(A))=EI(A)的最小距離d(A，B)的梯形模糊數。文獻[2]證明了t1、t2、t3、t4的值如下：

2 主要結果

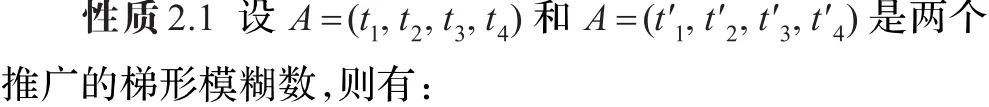
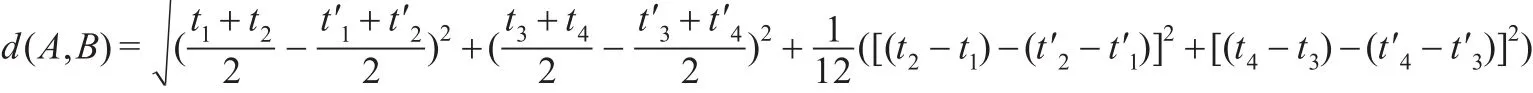
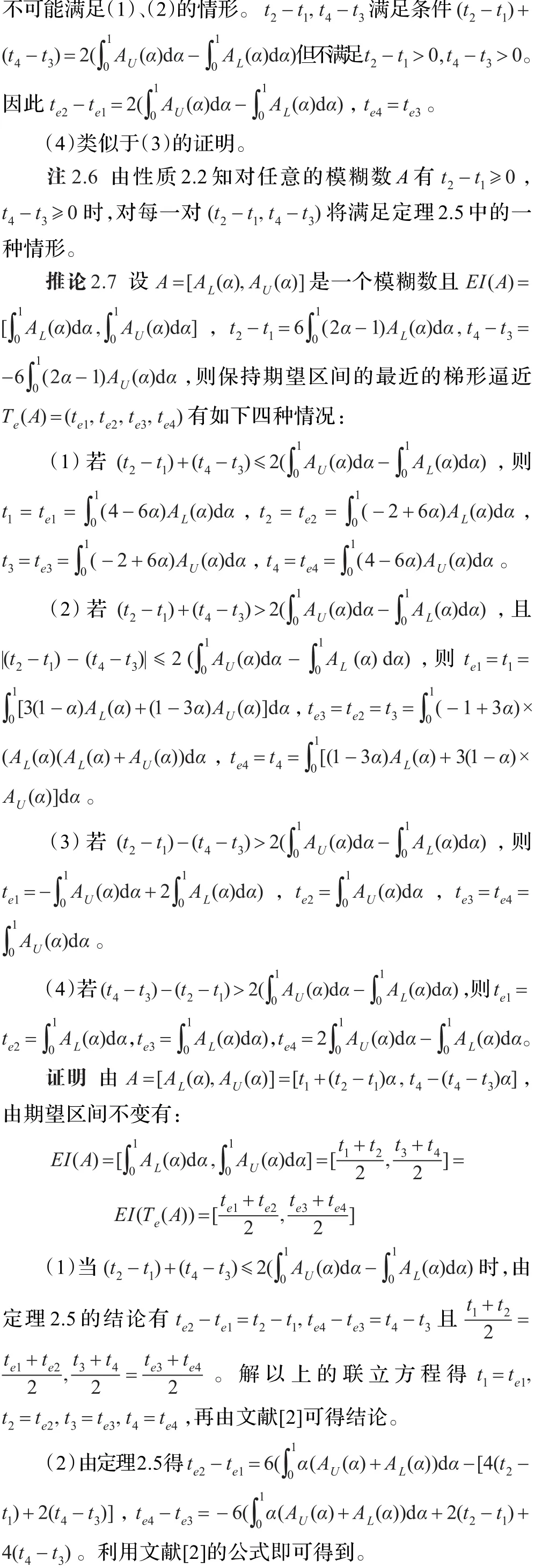
3 結束語

目前，模糊數已被廣泛地應用于自然科學、工程技術、社會科學等各個領域（實際上凡是涉及到模糊性的數量時都可以考慮用模糊數）。利用一個梯形的或三角的模糊數去逼近一般的模糊數引起了眾多學者的關注。本文推廣了梯形模糊數的一些性質，得到了更具體、更直觀的計算梯形逼近的方法。今后的研究中，還可以嘗試將[0，1]換成一般的取值格（如完全分配格），以便適用范圍更廣、更有代表性（涉及積分的地方可使用sugeno積分進行嘗試）。

[1]Zadeh L A.Fuzzy sets[J].Information and Control，1965，8：338-353.

[2]Grzegorzewski P，Mrówka E.Trapezoidal approximations of fuzzy numbers[J].Fuzzy Sets and Systems，2005，153：115-135.

[3]Grzegorzewski P.Metrics and orders in space of fuzzy numbers[J].Fuzzy Sets and Systems，1998，97：83-94.

[4]Dubois D，Prade H.The mean value of a fuzzy number[J]. Fuzzy Sets and Systems，1987，24：279-300.

[5]Heilpern S.The expected value of a fuzzy number[J].Fuzzy Sets and Systems，1992，47：81-86.

[6]Yeh C T.Trapezoidal and triangular approximations preserving the expected interval[J].Fuzzy Sets and Systems，2008，159：1345-1353.

[7]Allahviranloo T，Firozja M A.Note on“trapezoidal approximation of fuzzy numbers”[J].Fuzzy Sets and Systems，2007，158：755-756.

[8]Dubois D，Prade H.Operations on fuzzy number[J].International Journal of Systems Science，1978，9：613-626.

[9]Yeh C T.A note on trapezoidal approximations of fuzzy numbers[J].Fuzzy Sets and Systems，2007，158：747-754.

[10]Grzegorzewski P，Mrowka E.Trapezoidal approximations of fuzzy numbers-revisited[J].Fuzzy Sets and Systems，2007，158：757-768.

[11]Ban A I.Approximation of fuzzy numbers by trapezoidal fuzzy numbers preserving the expected interval[J].Fuzzy Sets and Systems，2008，159：1327-1344.

[12]Grzegorzewski P.Trapezoidal approximations of fuzzy numbers preserving the expected interval-algorithms and properties[J]. Fuzzy Sets and Systems，2008，159：1354-1364.

[13]Abbasbandy S，Hajjari T.Weighted trapezoidal approximation preserving cores of a fuzzy numbers[J].Computers and Mathematics with Applications，2010，59：3066-3077.

LU Hanchuan,LI Shenggang

College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China

This paper introduces the extended trapezoidal fuzzy number,and proves some properties of it.By using the extended trapezoidal fuzzy number to approximate any given fuzzy number,it is pointed that there are four cases on trapezoidal approximation,and a more detailed and more intuitive method to compute trapezoidal approximation and related examples are given.

fuzzy number;expected interval;the nearest trapezoidal approximation;extended trapezoidal fuzzy number

介紹了推廣的梯形模糊數并證明了它的一些性質。利用推廣的梯形模糊數逼近任意給定的一個模糊數，指出梯形逼近共有四種情形，給出了更具體、更直觀的計算最近的梯形逼近的方法和例子。

模糊數；期望區間；最近的梯形逼近；推廣的梯形模糊數

A

O159

10.3778/j.issn.1002-8331.1304-0097

LU Hanchuan,LI Shenggang.Trapezoidal approximations of fuzzy numbers.Computer Engineering and Applications, 2013,49（19）：16-19.

國家自然科學基金（No.11071151）；陜西省自然科學基金（No.2010JM1005）；陜西師范大學2012年研究生教育教學改革研究項目。

陸漢川（1977—），男，博士研究生，主要研究領域為格上拓撲學及擬陣論；李生剛（1959—），男，博士，教授，博士生導師，主要研究領域為格上拓撲學及擬陣論。E-mail：luhanchuan2004@163.com

2013-04-08

2013-06-03

1002-8331（2013）19-0016-04

CNKI出版日期：2013-06-18http://www.cnki.net/kcms/detail/11.2127.TP.20130618.1559.005.html