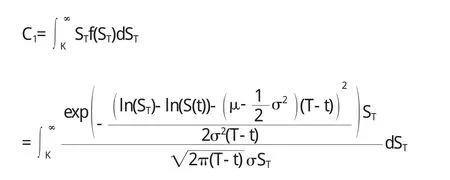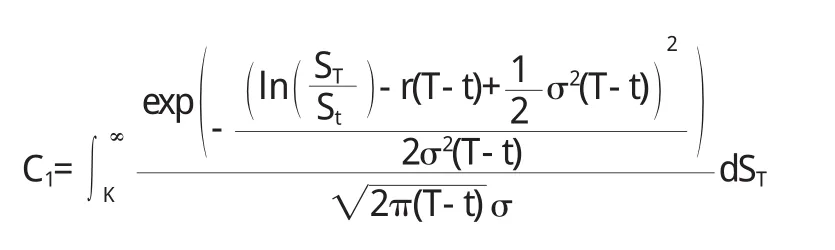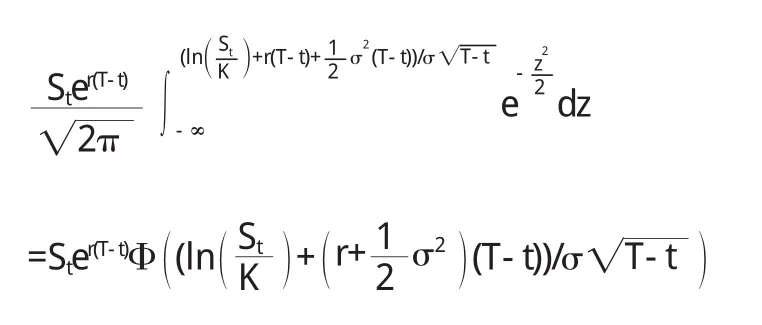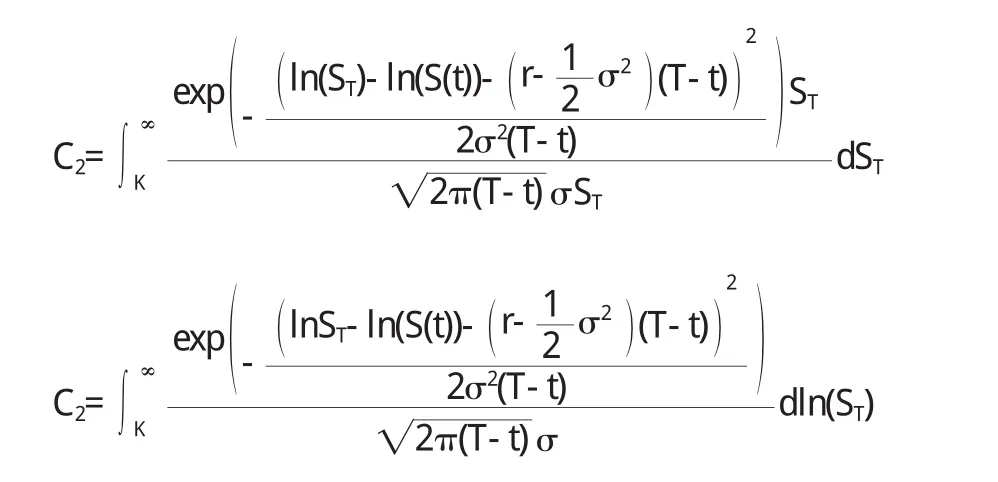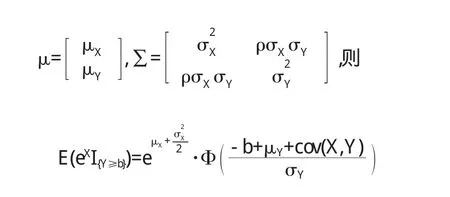金融數學中兩個基于高等數學的證明

李倩，張宇敬

（河北金融學院信息管理與工程系，河北保定071051）

金融數學中兩個基于高等數學的證明

李倩，張宇敬

（河北金融學院信息管理與工程系，河北保定071051）

近幾年，許多院校開設了面向數學系本科生的《金融數學》課程.本文作者結合一線教學經驗，就課程內容闡述了自己的觀點，并與讀者分享了教學過程中Black-Scholes模型和跳擴散模型中的數學推導.

金融數學；課程內容；Black-Scholes模型；高等數學證明

半個世紀以來，將量化分析引入金融學已經成為一種趨勢.金融數學作為數學、計算機、金融學的交叉學科受到業界和學界的重視.在此背景下河北金融學院信息管理與工程系為信息與計算科學專業大四的本科生開設了《金融數學》這門學科方向選修課.

為大四的本科生講授《金融數學》，既不能點到為止，提綱式教學，也不能面面俱到，令學生望而生畏.迄今為止，金融衍生品定價主要有兩種方法：偏微分方程方法和鞅定價方法.其中偏微分方程方法利用無套利原理構造資產組合，并用伊藤引理消去隨機項，從而建立起相應的偏微分方程.鞅定價方法的核心為以下原理：未來現金流的現值可以用其期望值按無風險利率貼現得到[1].

在制定教學大綱時，理論課分為兩大模塊：第一模塊以應用隨機分析為主線，包括：概率論基礎、布朗運動、泊松過程、伊藤積分、伊藤過程、伊藤公式、一階線性隨機微分方程、幾何布朗運動、等價鞅測度變換；第二模塊以期權定價模型為主線，包括：無套利原理、二叉樹模型、Black-Scholes期權定價模型和跳-擴散模型.理論課的兩大模塊是按照邏輯順序交差進行的.實踐課主要講授隨機模擬——蒙特卡羅法.

由于本門課程面向的是本科生，因而在一些細節問題中，做了與傳統教材不一樣的處理.下面舉兩個例子：

例如，講完一階線性偏微分方程后，引入Black-Scholes模型.

已知股票價格服從幾何布朗運動.

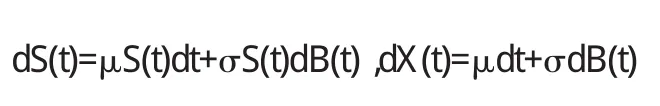
根據一階線性隨機微分方程的解法[2]

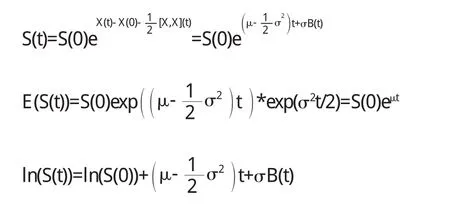
對其求導：

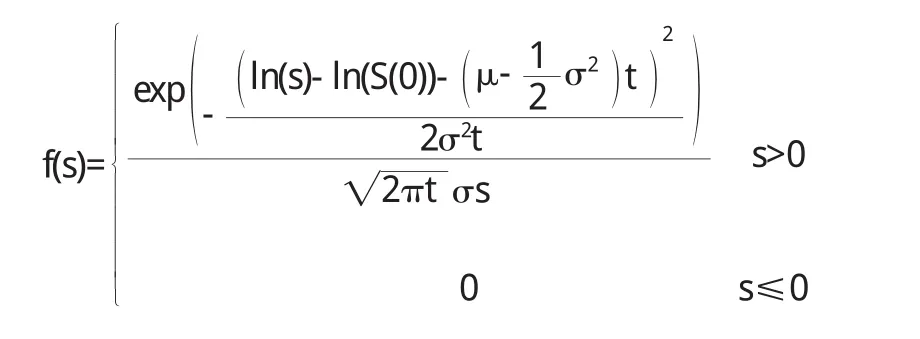
歐式看漲期權在T時刻的價格為CT=max(ST-K,0)，由鞅定價原理，在0≤t

先計算第一個積分：

由S(0)=e-rtE(S(t))，可以得到E(S(0))=e-rtE(S(t))，取對數，即

由E(S(t))=S(0)eμt，得到E(S(t))=eμtE(S(0))，取對數，即

兩式比較，得μ=r

由正態分布函數Φ(x)+Φ(-x)=1，原式化為

第二個積分：

令ln(ST)=y，原式化為

又比如，在求解跳-擴散模型時，需要證明以下引理[3]：若(X,Y)：N(μ,∑)，其中

原書中用的是標量計算，技巧性較強，學生不易接受，因此授課過程中采用矩陣計算.

坐標變換：

相應的Jaccobi行列式為

經簡單計算：v~N(0,1),u~N(0,1)

特別地

這種處理方式利用了矩陣的計算，既復習了高等代數中的知識，又提高學生運用矢量運算的意識，一舉兩得.

結論

學生通過學習《金融數學》，不僅溫習了先修課程：數學分析、高等代數、概率論和常微分方程，而且對隨機分析有了一定的理解，并對期權定價理論有了初步認識.不僅“溫故”，而且“知新”.

〔1〕孫健.金融衍生品定價模型[M].北京:中國經濟出版社，2008.

〔2〕Fima.K.Introduction to Stochastic Calculus w ith Applications[M].Imperial College Press 2008.

〔3〕奚李峰,樂安波，彭勃，等.金融數學[M].北京:清華大學出版社,2011.

O241.8

A

1673-260X（2013）09-0004-03