基于遺傳算法的配送車輛路徑規劃

郭秀紅

(長春職業技術學院 汽車分院，長春 130033)

城市配送系統(city delivery system，CDS)的發展是一個城市提高其公共運輸能力的關鍵。目前國內外許多學者對CDS 系統進行了深入研究［1-4］。其中，車輛路徑優化問題是城市配送系統中的重要環節，通過對車輛行駛路徑的優化管理可以有效地降低城市配送成本，同時可以提高城市交通效率，節省公共資源，無論對企業還是對社會，都具有重要的意義。本文針CDS 的車輛路徑規劃問題，采用遺傳算法(genetic algorithm，GA)作為優化方法，提出一種配送車輛路徑規劃的設計方案，以實現車輛路徑選取的最優決策。

1 配送車輛路徑規劃

1.1 城市配送系統

城市配送系統的功能構架如圖1 所示。城市配送系統是聯系供應商、信息中心、倉庫和消費者之間的重要紐帶。

城市配送系統的主要構成如圖2 所示，其中城市配送網絡子系統負責監管城市交通信息，城市配送運營調度系統負責對配送車輛進行調度，城市配送監管系統負責對配送車輛的任務執行情況進行監督管理和實時糾錯，城市配送信息處理系統負責對相關信息進行實時分析和處理。GDS 系統中較為關鍵的問題是在上述職能范圍內，如何構建一個最優運行框架來實現最優化的配送效益。

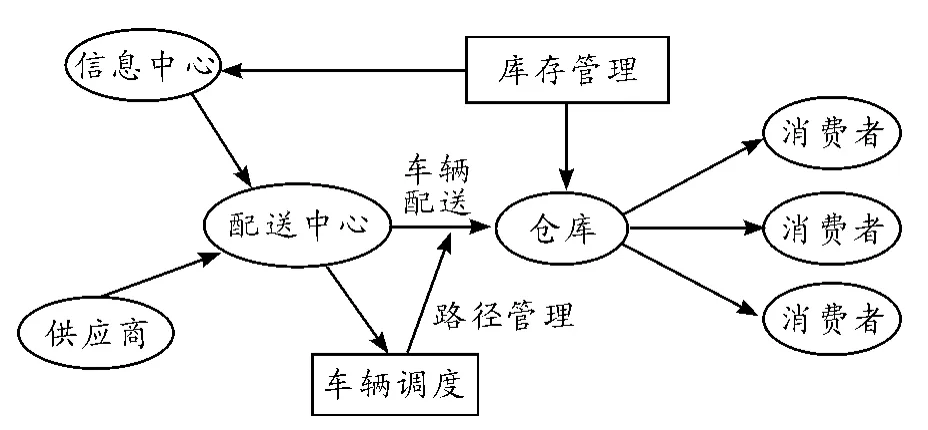
圖1 配送系統功能構架

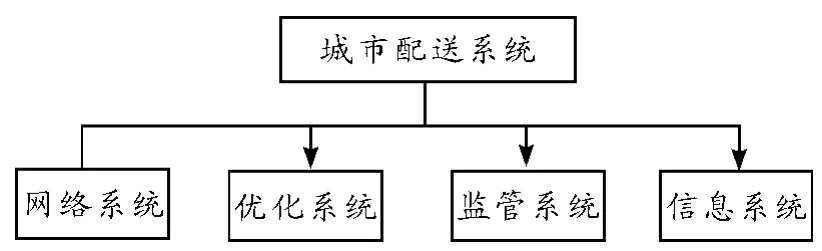
圖2 城市配送系統的組成

1.2 車輛路徑優化的意義

車輛路徑規劃(vehicle routing problem，VRP)自從1959年被Dantzig 和Ramse 提出的之后，迅速引起各領域工程師和管理學者的極大重視，成為工程管理領域的重點和熱點問題［1-3］。

VRP 問題是城市配送系統的主要優化問題之一，在城市配送系統中具有重要的意義。從企業運作和社會環保、節能的角度而言，VRP 研究的研究意義具體可以概括為以下方面:

1)通過對配送路線的合理優化，可以有效提高配送效率，從而縮短配送時間，提高服務質量和客戶滿意度;

2)通過對配送路線的合理優化，可以有效地降低運輸成本，節省資金;

3)有通過對配送路線的合理優化，可以有效降低車輛占用公路的時間，從而可以緩解交通，減少噪聲、尾氣排放等運輸污染。

2 VRP 問題的數學描述

為了便于研究VRP 問題的優化策略，首先對VRP 問題進行數學描述。假設配送中心和倉庫的地理位置均為固定且已知，則倉庫與配送中心以及倉庫間的位置信息可以由路徑距離矩陣描述為

VRP 可行解可以描述為一系列行駛路徑的決策的集合，即

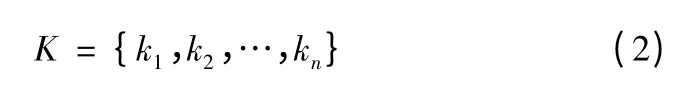
其中，ki表示第i 條路段決策結果。

VRP 優化目標由成本最小化來描述，即運輸過程中所產生的固定成本和運輸費用，如式(3)所示。

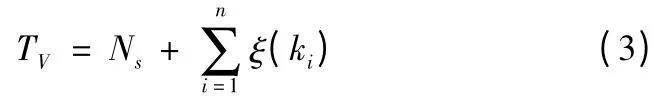
其中:TV為配送車輛在運輸過程中的總成本;Ns為運輸途中的固定費用;ξ(ki)為在第ki路段上的花費，正比于ki路段的行駛里程，計算式為

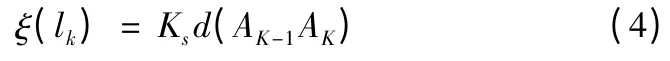
其中:d(·)為距離運算符;Ks為單位里程所需的費用;AK為倉庫節點標號。

考慮到在實際配送過程中有許多的條件限制，因此在目標函數上施加一定的約束條件，主要包括:車輛配送過程中所攜帶的貨物量存在上限，且車輛完成配送任務之后須返回出發點以備下次配送任務。

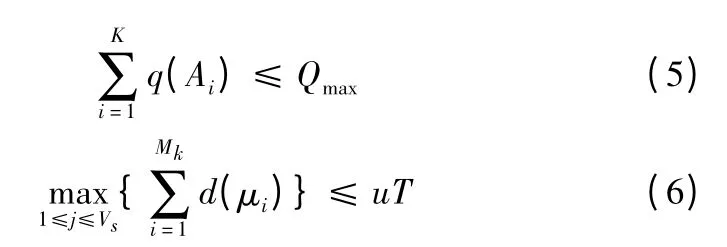
其中:Qmax為配送車輛承重上限;q(·)為載運重量計算符;u 為平均車速;T 為配送任務所要求的最大時間限度。

3 VRP 問題的遺傳算法優化

結合上述模型，基于遺傳算法來解決所提出的VRP 問題，基本參數設定為:種群M 為20，最大代數G 為100，交叉概率Pc 為0.8，變異概率Pm 為0.1，首先對VRP 問題的可行解進行編碼并生產初始種群，整個算法實施步驟如圖3 所示。根據目標函數設計適配度，終止條件設計為:

1)當最優解連續5 代不發生變化;

2)當迭代步數超過300 步。

對于初始種群根據數學模型的輸入條件，進行適配度計算并根據適配度計算結果進行種群選擇操作。

3.1 編碼規則

根據VRP 問題的特點，本文采用浮點數編碼方案，首先將各個倉庫的節點數轉換為相對應的隨機浮點數，同時將送貨中心(即配送過程的起點)作為第一個浮點數，考慮到編程的方便，將送貨中心同時作為終點放入到最后一個浮點數，計算式為

其中:s0為生產中心所對應的浮點數;s1～sn為n 個倉庫所對應的浮點數。

越小的浮點數對應有越高的優先級，例如對于染色體

其對應的表現型為

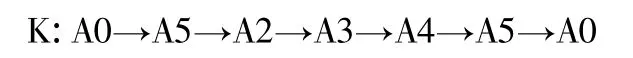
起點s0至為0.01，終點sn+1置為0.99，起點與終點參與編程，但不參與到選擇、交叉與變異。

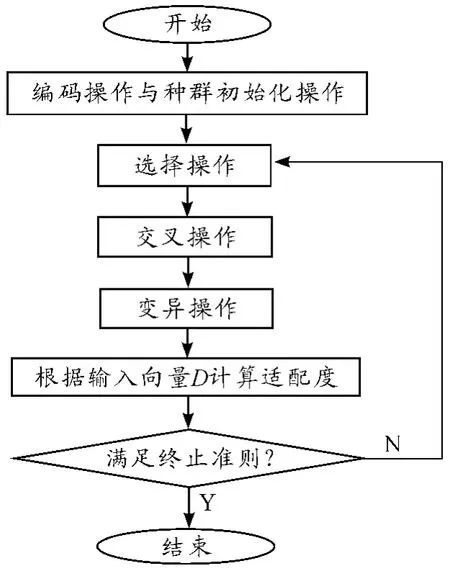
圖3 基于遺傳算法的算法流程

3.2 適配度函數

根據上述編碼規則，對每一個可行解都可以計算出整個配送過程中的行駛路線，將行駛總距離作為適配度函數其中χs表示第s 個可行解的適配度。

3.3 遺傳算子設計

在上述基礎上對遺傳算法進行選擇算子、交叉算子和變異算子的設計。

1)選擇算子

對種群中的20 個可行解根據適配度值來選擇排序靠前的10 個染色體作為選擇結果，放入后代中繼續后續操作。

2)交叉算子

對于選定的兩個父代個體，隨機選擇一個交叉位置，將其中一個父代中的前t 個基因作為子代個體的前t 個基因，同時將第2 個父輩染色體X2 的后n -t 個基因取出作為子代的后n-t 個基因，如圖4 所示。

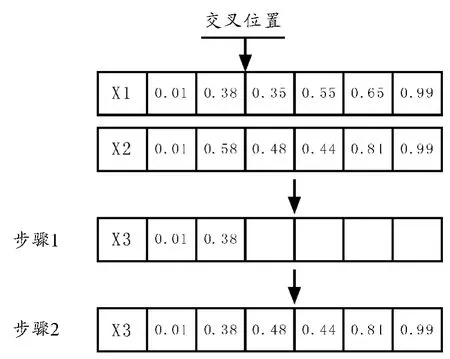
圖4 交叉操作示意圖

3)變異算子

首選按照變異概率來決定發生變異的位，然后變異操作采用取逆算子

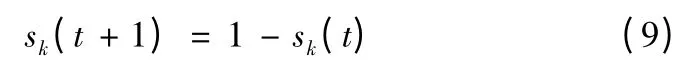
4 優化結果及分析

結合上述遺傳算法設計方案，在Matlab 環境中采用謝菲爾德GA 工具箱函數來進行算法實現，選擇算子采用select函數，交叉算子采用xovshrs 函數，變異算子采用mutate 函數，經過37 次迭代后算法收斂至最優解。

對應的表現型，即最優配送路徑為

將算法隨機生成的初始解對應的配送路徑與最優解所決定的規劃方案繪制成有向圖，如圖5 ～6 所示，從結果可以看出，可以有效完成配送路線的尋優任務，共節約行駛里程20 km。

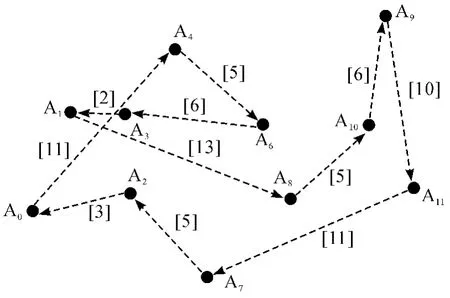
圖5 算法隨機生成的初始路徑

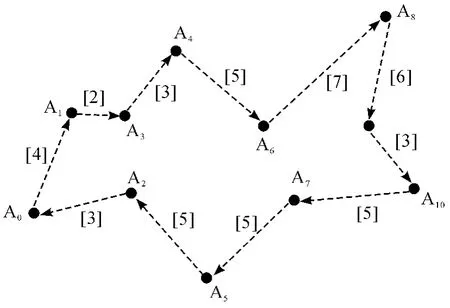
圖6 基于遺傳算法所確定的最優路徑

5 結束語

1)遺傳算法非常適合用于解決城市配送系統中的VRP問題，可以有效完成配送路線的尋優任務，從而降低配送過程中的運輸費用;

2)采用浮點數編碼并使用數值大小作為優先級決策的GA 算法設計方法正確有效，計算所得的最優路徑與初始路徑方案相比，節約行駛里程20 km。

［1］曹進.物流配送優化與跟蹤研究及系統實現［D］.哈爾濱:哈爾濱工業大學，2006.

［2］李冬梅. 物流配送車輛優化調度方法的研究與實現［D］.沈陽:沈陽工業大學，2007.

［3］Montemanni R，Gambardella L M，Rizzoli A E，et al. Ant Colony System for a Dynamic Vehicle Routing Problem［J］.Journal of Combinatorial Optimization，2005(4):327-343.

［4］張丹羽.現代物流配送中心車輛線路優化方案研究與應用［D］.濟南:山東大學，2005.