某火炮自動供彈機定位精度影響因素分析

趙搶搶，侯保林

(南京理工大學 機械工程學院，南京 210094)

某火炮自動供彈機是典型的鏈傳動機構，工作時由2 個電機并聯驅動鏈輪，帶動貯彈筒運動，將選定的彈丸輸送到指定位置。被選定彈丸停靠位置的精確度將直接影響自動供彈機運行的連續性與可靠性，為此需要對影響彈丸定位精度的重要因素進行分析。由于在實際情況下影響自動供彈機定位精度的因素非常多，每種情況都做分析并不現實，因此本文分析了3 種在實際使用過程中經常遇到的影響因素:彈筒內彈丸數目的變化、滾輪磨損脫落以及基礎擾動的影響，由此獲得了各參數對自動供彈機定位精度的具體影響情況。

1 仿真模型的建立

1.1 自動供彈機虛擬樣機的建立與簡化

自動供彈機是一個非常復雜的系統，為減少建模和求解過程中的人為錯誤，提高計算效率，需要在建立供彈機虛擬樣機時對模型進行簡化。由于在ADAMS 中模型外形并不影響計算結果，而三維模型的計算卻比二維模型要復雜得多，因此本文在ADAMS 中建立的供彈機模型為二維模型，各零件的質量和轉動慣量通過user input 的方式定義。根據供彈機各零部件間的拓撲關系，在ADAMS 中建立了主動輪、從動輪、供彈機支架、25 個彈筒、相應數量的滾輪以及減速箱。減速箱也進行了相應的簡化，包括小齒輪、大齒輪及蝸輪蝸桿4個剛體。虛擬樣機模型如圖1 所示。

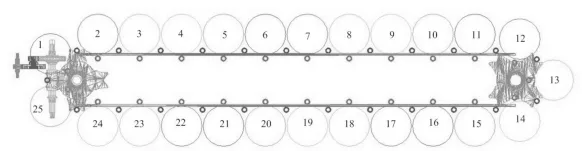
圖1 ADAMS 中建立的虛擬樣機模型

各部件拓撲關系如下:供彈機支架與慣性系固定;主動輪、從動輪與供彈機支架鉸接，有1 個旋轉自由度;小齒輪、大齒輪、蝸輪蝸桿都與供彈機支架鉸接，各有1 個旋轉自由度。小齒輪與大齒輪、大齒輪與蝸桿、蝸桿與蝸輪間通過齒輪副連接，同時蝸輪與主動輪固聯;每2 個相鄰彈筒間鉸接，有1 個旋轉自由度;每個彈丸與相應的彈筒固聯;每個滾輪與相應的彈筒鉸接，有1 個旋轉自由度，同時滾輪與供彈機支架、主動輪、從動輪實體接觸。驅動力矩加載在小齒輪上，其大小由simulink 中的控制系統輸入。

1.2 控制系統的建立

當把所有構件都看做剛體時，彈倉表現為一單自由度剛體系統。取主動輪為等效構件，可用單自由度系統的等效方法來建立彈倉的運動方程

其中，Me為等效力矩

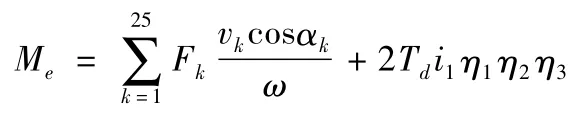
式中:Fk(k=1，2，…，25)為作用在彈筒上的外力;vk為外力Fk作用點的速度;αk為Fk作用方向和vk方向之間的夾角;Td為電機的驅動力矩;i1、i2和i3分別為總傳動比、小齒輪和大齒輪到蝸輪的傳動比以及蝸輪蝸桿的傳動比;η1、η2和η3分別為對應各傳動比的機械傳動效率;ω=dθ/dt 為等效構件(主動輪)的角速度。

等效轉動慣量為

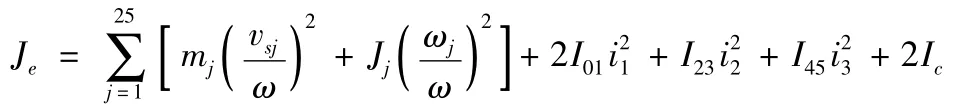
式中:ωj為第j 個彈筒的角速度;vsj為第j 個彈筒質心的速度;I01、I23、I45及Ic分別為電機和小齒輪、大齒輪、蝸桿以及蝸輪和主動輪的轉動慣量，從動輪的轉動慣量與主動輪相同。

其中，等效力矩Me由電機驅動力矩、制動力矩等效于主動輪上的力矩、重力作用于彈筒上形成的等效力矩、作用于各構件上的摩擦力形成的等效力矩等各項構成。

在實際控制中，采取在電機一啟動就開始進行反饋控制的方法是比較難實現準確定位的。根據本文的實際情況，采取如下控制策略:當待發射彈丸快要到位時，才開始實施反饋控制，而對彈筒在前面時間的運動，僅讓電機拖動系統自由運行，盡量使得在各種情況下的位置控制起點和彈筒運動速度相同或相近。本文控制目標為主動輪旋轉180°，即彈筒旋轉2 個彈距，每個彈距185 mm。在接近目標值前45°時實施反饋控制。由此，得出系統的控制框圖如圖2 所示。

圖2中，方框表示自動供彈機的機械系統(動力學模型見圖1)，電機用狀態矩陣的形式表示，電機的基本參數為:R=0.3，La=0.02，k?=0.035，KT=0.035。

在傳動元件中，用效率標識齒輪傳動間的摩擦影響，取滾輪與軌道間的摩擦系數為0.1。取第1 級、第2 級的傳動效率η1、η2均為0.95，蝸輪蝸桿的傳動效率為0.5。

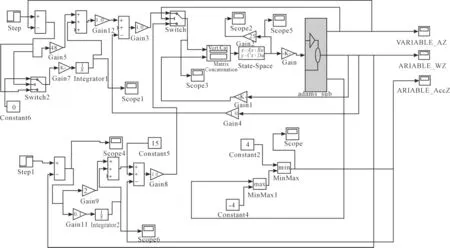
圖2 控制系統框圖

2 計算分析結果

2.1 彈筒內彈丸數目不確定的影響

彈筒內彈丸數目的變化是造成自動供彈機控制復雜的1個重要因素。實際中，彈筒內彈丸數目的變化情況復雜，不可能一一進行分析，為此本文選擇了4 種極端情況:①彈筒全部滿載;②彈筒全部空載;③上軌道有12 發彈筒不帶彈丸;④下軌道有12 發彈筒不帶彈丸。通過比較這4 種極端情況下系統定位精度的差別，以了解系統的變化特性。為方便比較，選擇只做平動的4 號彈筒為參考。圖3 ～圖6 給出了4 種情況的若干計算結果。

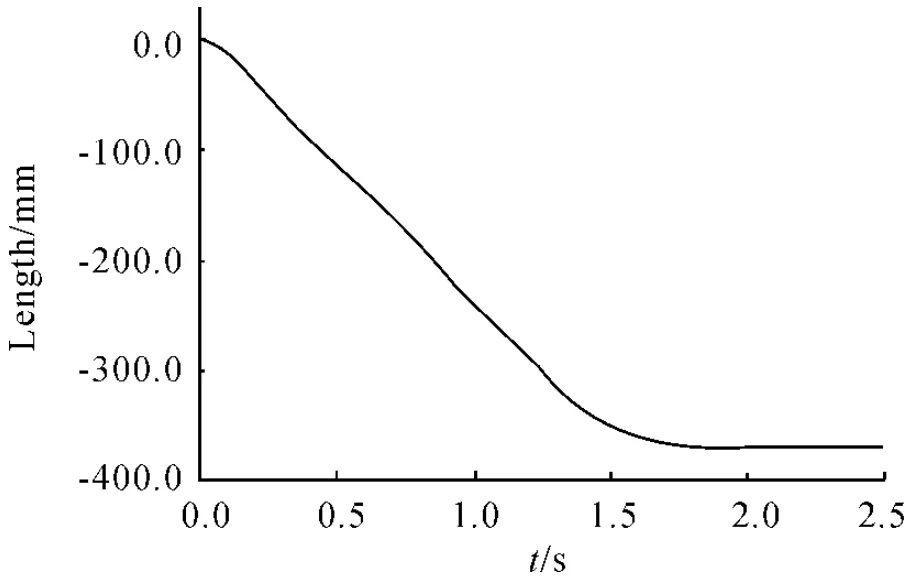
圖3 滿載4 號彈筒位移

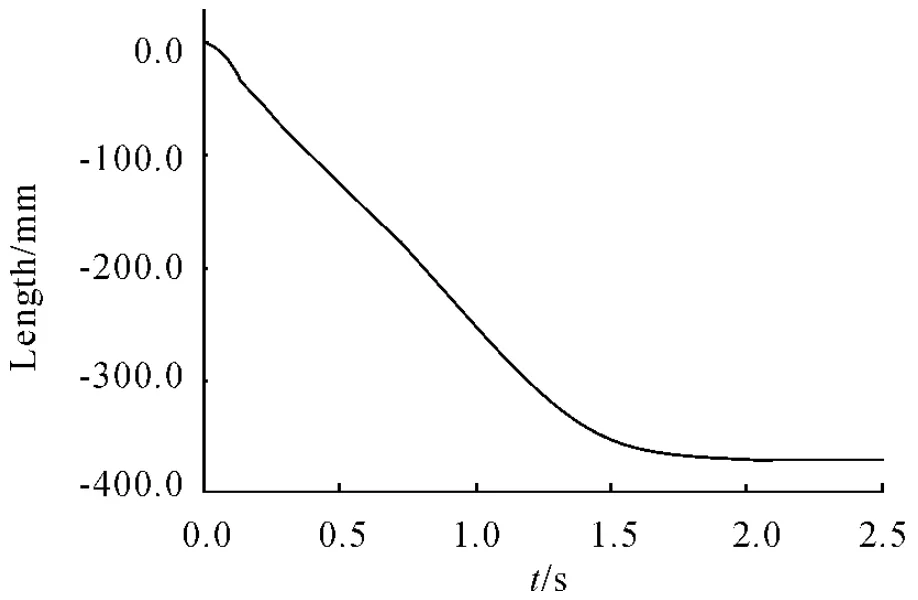
圖4 空載4 號彈筒位移

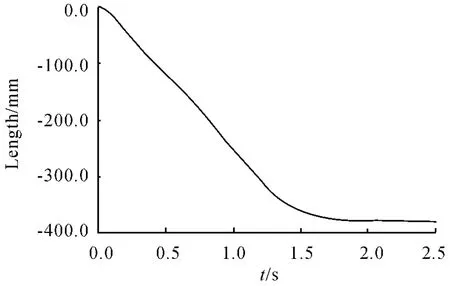
圖5 軌道滿載4 號彈筒位移

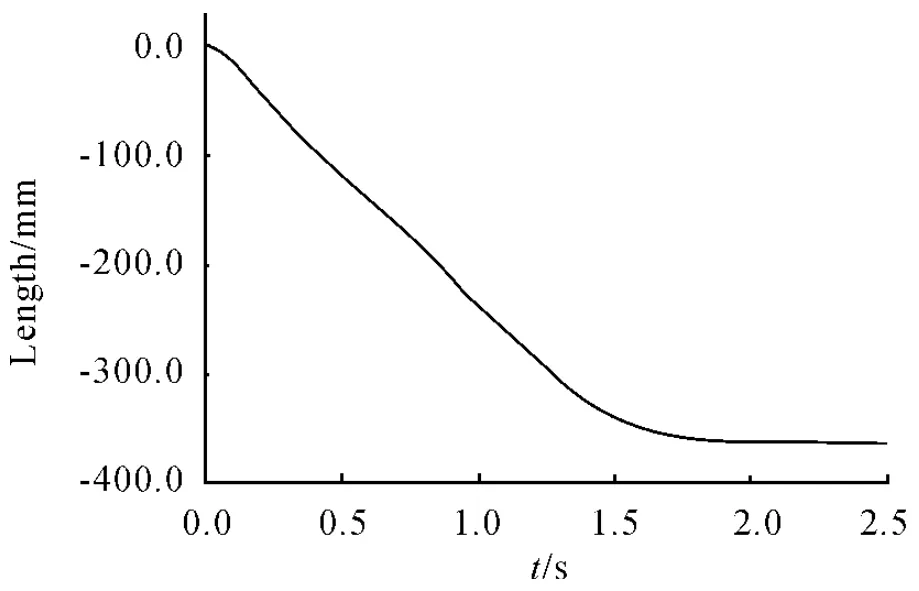
圖6 下軌道滿載4 號彈筒位移

根據圖3 ～圖6，可得出對比結果見表1。

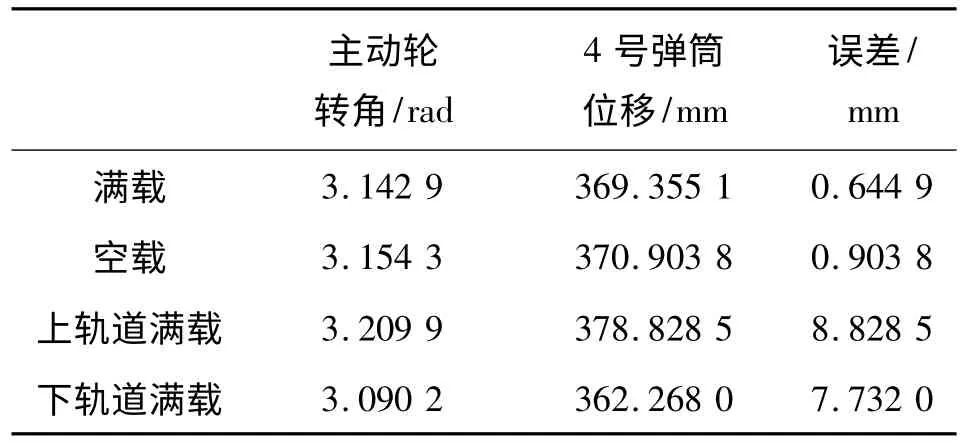
表1 不同負載下計算結果對比

比較上述結果可以發現:彈筒內彈丸數目不同，將導致系統等效轉動慣量不同，同時導致系統所受阻力矩也不同。其直接結果就是使得系統定位精度不穩定。由此可以確定，彈筒內彈丸數目的不同，會直接影響自動供彈機的定位精度，且影響較大。

2.2 滾輪磨損掉落的影響

實際情況中，滾輪所用材料為尼龍。根據使用情況來看，在使用一段時間后，滾輪可能會開裂而脫落，從而導致滾輪軸直接與主從動輪及導軌接觸。考慮到主動輪與滾輪接觸時沖擊振動比較大，為模擬真實的情況，假設模型中與主動輪接觸的滾輪掉落2 個，在此選擇1 號彈筒和24 號彈筒滾輪脫落，整個模型滿載。

修改模型后的計算結果如圖7 所示。

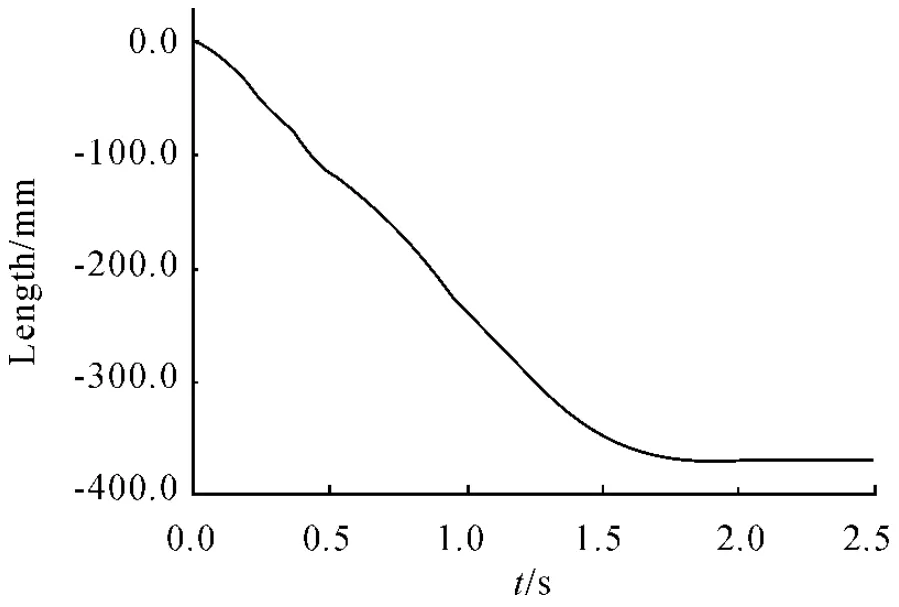
圖7 滾輪脫落后4 號彈筒位移

滾輪脫落后，主動輪轉角位3.142 rad，彈筒位移為369.308 7 mm，其定位誤差為0.691 3 mm。可見滾輪脫落對自動供彈機定位精度的影響并不大。但仔細比較滿載情況下滾輪沒有脫落的位移曲線和滾輪脫落后的位移曲線可以發現，滾輪脫落后的位移曲線并不如未脫落前的位移曲線光滑。這是因為滾輪脫落后，主動輪直接與滾輪軸接觸，配合存在間隙，使得其接觸時沖擊振動比較大，自動供彈機雖能比較準確定位，但其運動過程卻不夠平穩。

2.3 基礎擾動的影響

在某火炮的實際使用過程中，裝填的過程并不一定處于停車狀態，很多時候需要在運動中進行裝填，或者在發射后裝填，因此自動供彈機在運行時經常會受車身振動的影響。根據以往所做實驗獲得的車身振動曲線，給系統在y 方向添加1 個強迫位移來模擬現實中的擾動情況，其大小如圖8所示。

圖8 添加于系統的基礎擾動

在滿載情況下，計算結果如圖9 所示。

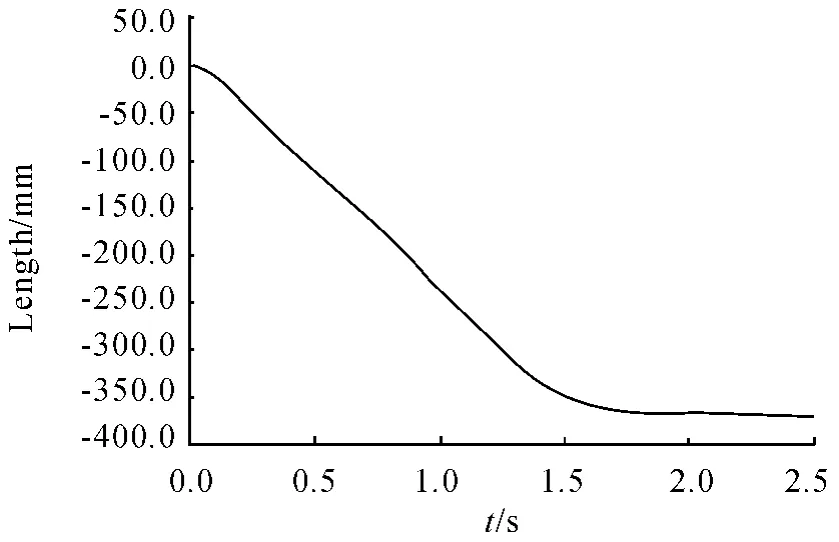
圖9 存在基礎擾動的4 號彈筒位移

在存在基礎擾動的情況下，主動輪轉角為3.143 9 rad，彈筒位移為369.518 9 mm。因此，在基礎擾動并不太大的情況下，擾動對自動供彈機定位精度的影響并不明顯。但觀察4 號彈筒在y 方向的位移(圖10)可發現，4 號彈筒在y 方向的位移曲線明顯不如添加的基礎擾動曲線光滑，說明在添加基礎擾動之后，彈筒在y 方向會發生跳動，明顯影響自動供彈機的運行穩定性。

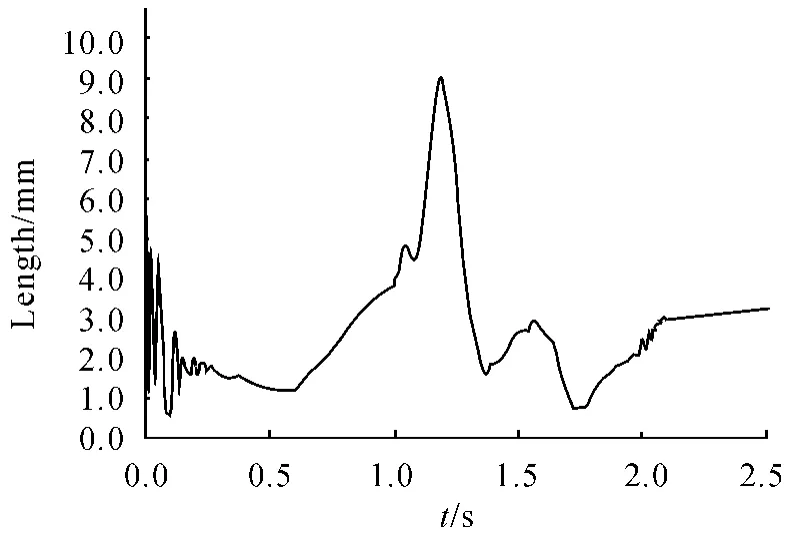
圖10 4 號彈筒在y 方向的位移

3 結束語

分析比較3 種不同情況下自動供彈機的定位誤差可知:彈筒內彈丸數目的變化是影響供彈機定位誤差的主要因素，彈筒內彈丸數目不同，供彈機定位精度差別明顯;在實際使用中，若能及時檢查更換脫落的滾輪，保證滾輪脫落數不多，并不會對自動供彈機的定位精度有很大影響，但滾輪脫落會導致自動供彈機運行不穩定，產生沖擊振動;實際使用過程中，系統的基礎擾動不會對自動供彈機的定位精度產生明顯影響，但會導致供彈機運行不穩定，產生明顯的振動。

［1］侯保林，樵軍謀，劉琮敏.火炮自動裝填［M］.北京:兵器工業出版社，2010:217-218.

［2］石明全.某火炮自動供彈機橫向振動特性研究［J］.彈道學報，2002，12(3):42-46.

［3］樊永生，余紅英，潘宏俠.某自行火炮自動裝填系統供彈機運動學 分析［J］.華北工學院學報，1999，20(3):269-272.