φ混合序列乘積和的強大數(shù)定律

曹正芳

（湖北大學 數(shù)學與計算機科學學院，湖北 武漢 430062）

φ混合序列乘積和的強大數(shù)定律

曹正芳

（湖北大學 數(shù)學與計算機科學學院，湖北 武漢 430062）

建立了φ混合序列的矩不等式，利用這個不等式得到了φ混合序列的三級數(shù)定理及乘積和的強大數(shù)定律。

φ混合序列；三級數(shù)定理；乘積和；強大數(shù)定律

1 預備知識

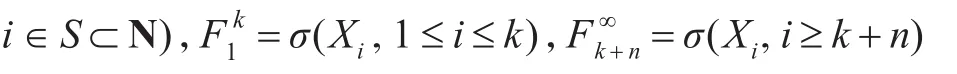
設{Xn，n≥1}是定義在概率空間(Ω，F(xiàn)，P)上的隨機變量序列，記為σ域，其中N為自然數(shù)集，記Lp(F)為所有F可測且 P階絕對矩有限的隨機變量全體。在 F中給定σ域B和R，令

對于隨機變量序列{Xn，n≥1} ，如果有 φ(n)=則稱{Xn，n≥1} 為 φ混合序列。

φ混合序列的概念由Dobrushin［1］于1956年在研究馬氏過程中引入，由定義可知φ混合序列是一類非常廣泛的隨機變量序列。通常的獨立隨機變量序列可看成是φ混合序列的特殊情形，因此對于φ混合序列的研究十分困難。自從引入了φ混合序列的概念，不少學者研究了φ混合序列的大數(shù)定律，獲得了類似于Marcinkiewicz強大數(shù)定律［2-3］。近年來，一些學者開始研究不同分布的混合序列的大數(shù)定律［4-5］。本文主要在的條件下構(gòu)造φ混合序列的矩不等式，用這個不等式得到φ混合序列的三級數(shù)定理及乘積和的強大數(shù)定律。

本文約定：以下出現(xiàn)的C總表示正常數(shù)，它在不同的地方可以代表不同的值。

引理1［4］設為φ混合序列，X∈ Lp()，Y∈Lq(F)，其中 p，q≥1且1/p+1/q=1，則

引理2［6］對任意的實數(shù)列{Xn，n≥1}，及對任意的n≥m≥1，有

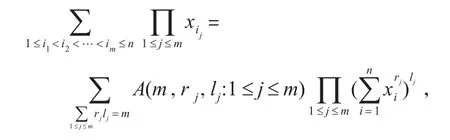
特別地，對任意的n≥1，有

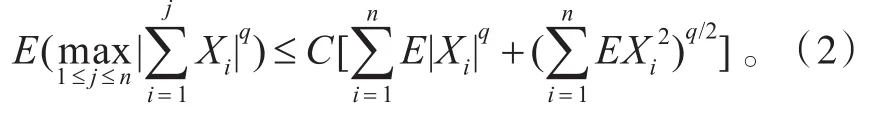
證明 由引理1，取 p=q=2，得到

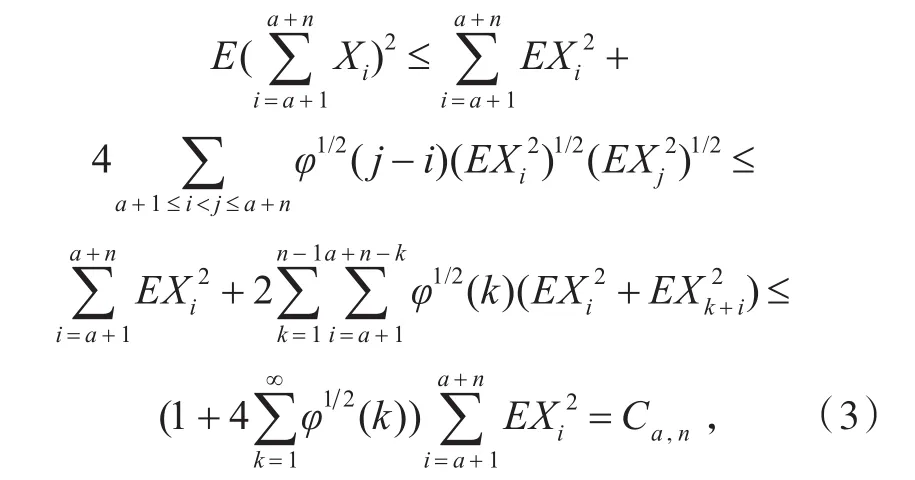
再由文獻［7］可知（1）式成立。

2 主要結(jié)果及其證明

定理1 設{Xn，n≥1}為 φ混合序列，滿足假設

證明 不失一般性，假設 EXn=0，n≥1，又設m＜n為正整數(shù)，由（3）、（4）式得

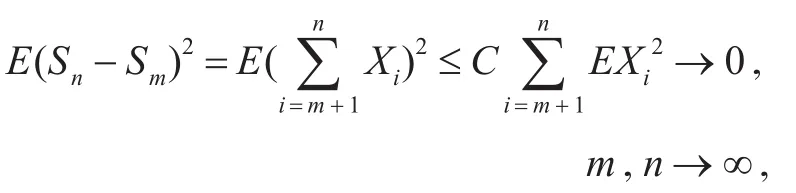
即{Sn，n≥1}是 L2中的Cauchy序列。故存在一個隨機變量 S∈L2，使得亦即因此存在一個正整數(shù)nk→∞，使得Snk→S a.s.，k→∞。由子序列構(gòu)造法，只需證明

事實上，對任意的ε＞0，由Markov不等式及（2）、（4）式得(令n0=0)

由Borel-Cantelli引理知（5）式成立。

定理1得證。

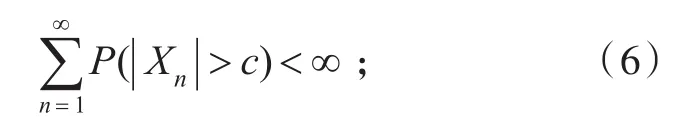
（i）gn(x)在(0，∞)內(nèi)單調(diào)不減，且當0＜x≤1時，gn(x)≥λxθ(0＜θ≤1)；

其中0＜α≤1，β≥1。

同時對于正常數(shù)序列{an，n≥1}，滿足an↑∞，及當 p∈[1，2)時，若

進一步地，對任意的m≥1，

證明 先證（9）式。令Xn′=XnI(| Xn|＜)，則故仍為φ混合序列。

在條件（i）下，gn(x)在(0，∞)內(nèi)不減，以及gn(1)≥λ。

因此由Borel-Cantelli引理及條件（i）、（ii），得到隨機變量序列{Xn，n≥1}、{Xn′，n≥1}是尾列等價的。

于是要證（9）式成立，只需證明

僅在條件（ii）下給出證明過程，在條件（i）下證明類似。

首先，對任意的n≥1，

所以由Kronecker引理知

于是，只需證明

由于

故（9）式成立。

接下來，對給定的m≥1，由引理2可知，欲證（10）式成立，只需證明對任意的1≤r≤m，都有

由Cr不等式得

從而要證（13）式對r=1，2，…，m成立，只需證明（13）式對 r=1，2成立即可。其中當 r=1時，上述已證。當r=2時，由Borel-Cantelli引理及（11）式，只要證

于是，由Kronecker引理知（14）式成立。

綜上所述，定理3得證。

推論1 設{Xn，n≥1}為 φ混合序列，滿足是正常數(shù)序列，滿足an(x)↑∞，同時下列條件之一成立：

①當0＜r＜1時，有

②當1≤r≤2時，有

且EXn=0，n≥1，則

進一步地，對任意的m≥1，有

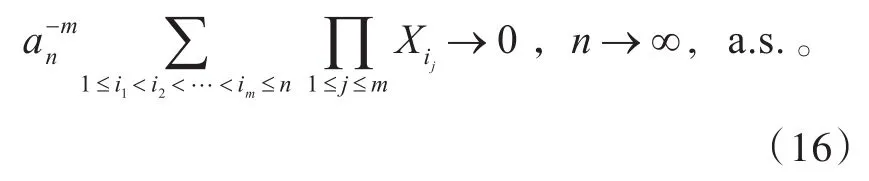
證 明 當條件①成立時，取 gn(x)= |x|r/(1+|x|r)，0＜r＜1；當條件②成立時，取gn′(x)=|x|r/(1+|x|r-1)，1≤r≤2。那么對任意的n≥1，gn(x)、gn′(x)均為偶函數(shù)，且在(0，∞)內(nèi)取正值，不減，并且 gn(x)≥xr/2，0＜x≤1，0＜r＜1；gn′(x)≥xr/2，0＜x≤1，1≤r≤2；gn′(x)≥x/2，x＞1。

因此，若滿足條件①，則

若滿足條件②，則

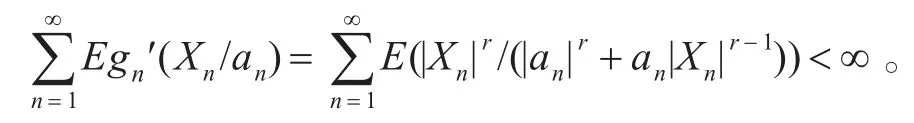
于是由定理3可知推論1成立。

由推論1可得：

推論2 設{Xn，n≥1}為 φ混合序列，滿足是正常數(shù)序列，滿足且當r∈(1，2]時，EXn=0，n≥1，則（15）、（16）式成立。

［1］ Dobrushin R L.The central limit theorem for non-sta?tionary Markov Chain［J］.Theorey Probab Appl，1956（1）：72-88.

［2］ 薛留根.混合序列強大數(shù)定律的收斂速度［J］.系統(tǒng)數(shù)學與科學，1994，14（3）：213-221.

［3］ 萬成高，陳芬.一類相依隨機變量序列乘積和的Mar?cinkiewicz型強大數(shù)定律［J］.數(shù)學研究，2008，41（2）：168-174.

［4］ 林正炎，陸傳榮.混合相依變量的極限理論［M］.北京：高等教育出版社，1997.

［5］ 吳群英.混合序列的概率極限理論［M］.北京：科學出版社，2006.

［6］ 王岳寶，嚴繼高，成鳳旸，等.關于不同分布的兩兩NQD列的Jamison型加權(quán)乘積和的強穩(wěn)定性［J］.數(shù)學年刊，2001，22A（6）：701-706.

［7］ Shao Q M. Almost sure invariance principles for φ-mixing sequences of random variables［J］.Stochas?ticProcessesand TheirApplications，1993，48：319-334.

Strong Law of Large Numbers of Sum of Products for φ-mixing Sequence

CAO Zheng-fang
（School of Mathematics and Computer Science，Hubei University，Wuhan 430062，Hubei，China）

Studies the moment inequalities forφ-mixing sequence，with the moment inequali?ties，obtains the three series theorem forφ-mixing sequence and the strong law of large numbers of sum of products.

φ-mixing sequence；three series theorem；sum of products；strong law of large numbers

O211.4

：A

：1673-0143（2013）02-0010-04

（責任編輯：強士端）

2012－12－17

曹正芳（1986—），女，碩士生，研究方向：金融數(shù)學。