基于免疫粒子群優(yōu)化的不等時間間隔發(fā)動機性能綜合指數(shù)組合預測

李冬，馬力，樊照遠，宋巖

基于免疫粒子群優(yōu)化的不等時間間隔發(fā)動機性能綜合指數(shù)組合預測

李冬1，馬力2，樊照遠2，宋巖3

(1.海軍航空工程學院研究生管理大隊，山東煙臺264001；2.海軍駐沈陽地區(qū)發(fā)動機專業(yè)軍事代表室，遼寧沈陽110015；3.海軍航空工程學院基礎實驗部，山東煙臺264001)

首先利用奇異值分解濾波算法，對測量參數(shù)進行濾波處理，進而合成發(fā)動機性能綜合指數(shù)。針對性能綜合指數(shù)為不等時間間隔的情況，在改進灰色預測模型中引入新陳代謝思想，提出一種基于免疫粒子群優(yōu)化權值的改進灰色模型與支持向量機相結合的性能指數(shù)預測方法。仿真實例表明：組合模型的預測精度明顯高于改進灰色預測模型，略高于支持向量機模型；且對于大多數(shù)樣本點，組合模型的預測結果變化更加平穩(wěn)。

不等間隔；發(fā)動機性能綜合指數(shù)；改進灰色模型；支持向量機；免疫粒子群優(yōu)化；組合預測

1 引言

發(fā)動機性能綜合指數(shù)是反映發(fā)動機性能狀況好壞的重要指標，預測其性能指數(shù)變化趨勢對開展發(fā)動機視情維修具有重要的指導意義。文獻[1]～[3]采用綜合指數(shù)加權法，融合多個表征發(fā)動機性能變化的參數(shù)，并且參數(shù)的權重以一定的優(yōu)化策略或方法獲取，最終以發(fā)動機性能指數(shù)單參數(shù)的形式表征出發(fā)動機的性能狀況。文獻[4]利用組合線性回歸模型的方法預測反映發(fā)動機性能變化的指標——起飛排氣溫度裕度，但存在預測精度不高的問題。文獻[5]對多臺發(fā)動機工作參數(shù)進行綜合加權，得到反映發(fā)動機性能的綜合指數(shù)，以最終誤差預報準則優(yōu)選嵌入維數(shù)，通過回歸支持向量機多步預測發(fā)動機性能綜合指數(shù)，來監(jiān)控發(fā)動機整機性能。文獻[6]基于改進灰色預測模型預測液壓泵壽命，文獻[7]基于非等間隔灰色模型預測捷聯(lián)慣組誤差系數(shù)，都取得了不錯效果。

鑒于支持向量機具有預測精度高、泛化能力強的優(yōu)點，和不需要較大樣本、適用于中短期預測的特點，灰色預測模型具有要求的數(shù)據(jù)量少、子樣小、短期預報精度高的優(yōu)點，本文綜合上述預測方法的特點，針對不等時間間隔性能指數(shù)具有非線性、非平穩(wěn)性的特點，采取兩種模型的組合預測，以免疫粒子群算法優(yōu)化其權重，對發(fā)動機性能指數(shù)進行預測研究。

2 發(fā)動機性能綜合指數(shù)合成

2.1發(fā)動機性能參數(shù)濾波

在實際發(fā)動機性能監(jiān)控中，反映發(fā)動機運行狀態(tài)的參數(shù)很多，但實際條件的復雜性，使得這些熱力參數(shù)與發(fā)動機性能狀態(tài)的對應關系具有一定的不確定性和模糊性。由于發(fā)動機性能衰退隨著使用時間的增加而逐漸增加，所以應選擇與飛行時間相關的性能參數(shù)作為表征發(fā)動機性能狀況的參數(shù)。由于發(fā)動機監(jiān)控參數(shù)的選擇受傳感器可安裝數(shù)量及位置限制，再考慮到實際可獲取的參數(shù)，確定低壓轉子換算轉速n1cor、高壓轉子換算轉速n2cor、渦輪后燃氣溫度T4等作為發(fā)動機性能監(jiān)控參數(shù)，并將數(shù)據(jù)做歸一化處理。收集發(fā)動機測量參數(shù)數(shù)據(jù)，近似為等間隔數(shù)據(jù)。如果出現(xiàn)測量參數(shù)間隔較大的情況，利用樣條函數(shù)插值轉化為等間隔數(shù)據(jù)，并對插值結果進行檢驗。采用奇異值分解濾波算法[8]，對發(fā)動機測量參數(shù)進行濾波，濾除參數(shù)中的隨機噪聲干擾，得到發(fā)動機測量參數(shù)穩(wěn)定的成分。濾波閥值為0.97。

2.2發(fā)動機性能綜合指數(shù)的合成

在穩(wěn)定測量參數(shù)基礎上，得到發(fā)動機性能綜合指數(shù)，見圖1。具體計算過程參見文獻[5]。

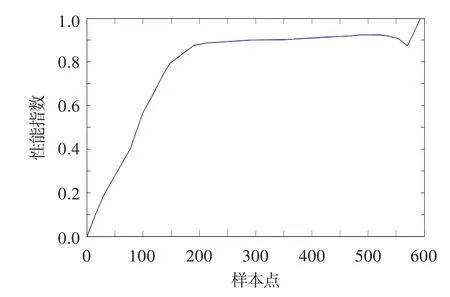
圖1 發(fā)動機性能綜合指數(shù)Fig.1 Engine performance synthetical index

3 基于免疫粒子群優(yōu)化的性能綜合指數(shù)預測

3.1改進的灰色預測模型

傳統(tǒng)的灰色預測是針對等時間間隔樣本的情況，對于不等時間間隔的發(fā)動機性能指數(shù)，應對原灰色模型加以改進。由于灰色模型的擬合和預測精度取決于背景值的構造形式，因此對背景值加以改進，具體改進方法參見文獻[6]。同時，在預測中引入新陳代謝思想，具體步驟為：

Step1：利用發(fā)動機性能指數(shù)訓練數(shù)列[x(0)(k1)，x(0)(k2)，…，x(0)(kk)]，求取此時對應的灰色模型的參數(shù)a和b，建立灰色預測模型。

Step2：通過公式(1)[6]得到最近一個預測數(shù)據(jù)(0)(kk+1)。

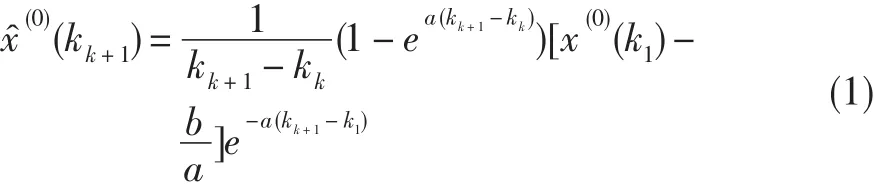
式中：k為不等時間間隔對應時刻，x?為預測值。

Step4：利用新數(shù)列重建灰色預測模型，并對a和b進行修正，然后轉到Step2。重復此過程，直到得到所有的預測參數(shù)。

3.2支持向量機預測模型

采取相空間重構方法，利用訓練數(shù)據(jù)建立支持向量機回歸預測模型。此時訓練數(shù)組為[y(0)(k2)，i=2，…，k。具體支持向量機模型的輸入和輸出形式如式(2)所示。

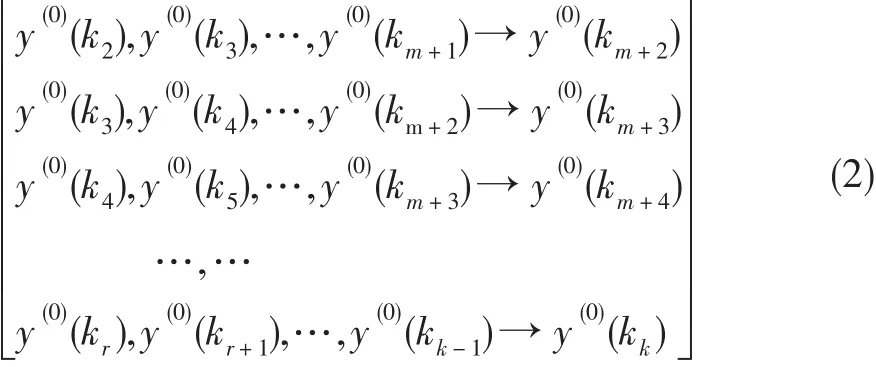
式中：r=k-m，m為嵌入維數(shù)。采取類似3.1節(jié)中灰色預測模型中的新陳代謝思想，依次求取所有預測參數(shù)[y?(0)(kk+1)，y?(0)(kk+2)，…，y?(0)(kn)]。在此基礎上，利用式(3)還原預測數(shù)據(jù)。式中：i=k+1，…，n。

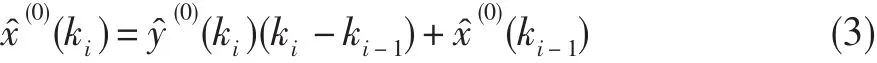
3.3基于免疫粒子群優(yōu)化的組合預測方法

考慮到非等時間間隔的性能指數(shù)呈非線性、非平穩(wěn)性特征，并且單個模型的預測精度不夠高，因此采用基于免疫粒子群優(yōu)化的改進灰色模型和支持向量機預測發(fā)動機性能綜合指數(shù)，以提高預測精度。本文的預測采用上述兩種預測模型，記n個實際觀測值yi(i=1，2，…，n)，第j種模型的第i個預測值為fij(j= 1，2)，預測誤差為eij=yi-fij，每種預測模型的權重為wj，則有：

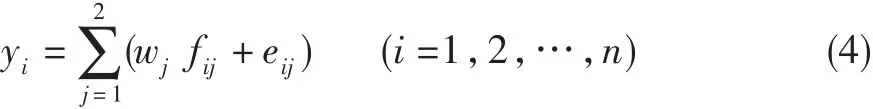
設w?j為權的估計值，y?i為組合預測值，則：

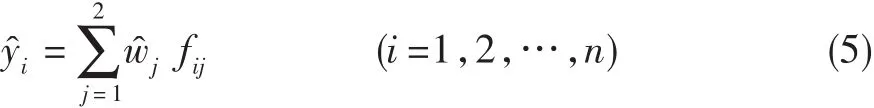
以絕對誤差和最小為優(yōu)化目標，即為免疫粒子群優(yōu)化算法中的適應度函數(shù)，見式(6)。其值越小，預測模型越接近于最優(yōu)。

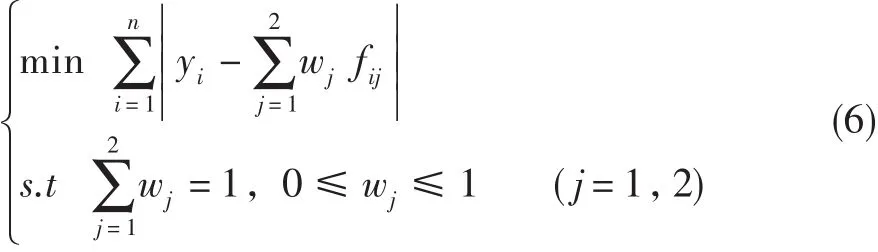
基于免疫粒子群優(yōu)化的組合預測發(fā)動機性能綜合指數(shù)的方法如圖2所示，具體流程為：

Step1：確定發(fā)動機測量數(shù)據(jù)，將測量參數(shù)融合成性能指數(shù)(圖1)，再將得到的性能指數(shù)分成兩部分，分用于建立預測模型和驗證模型；

Step2：分別利用灰色預測模型和支持向量機模型對圖1中性能進行訓練，在訓練中引入新陳代謝思想，直至得到所有預測值；

Step3：基于免疫粒子群算法優(yōu)化組合預測模型的權重系數(shù)，并以式(6)為優(yōu)化算法的適應度函數(shù)；

Step4：模型優(yōu)化結束，獲得最優(yōu)權重系數(shù)，確定組合模型。

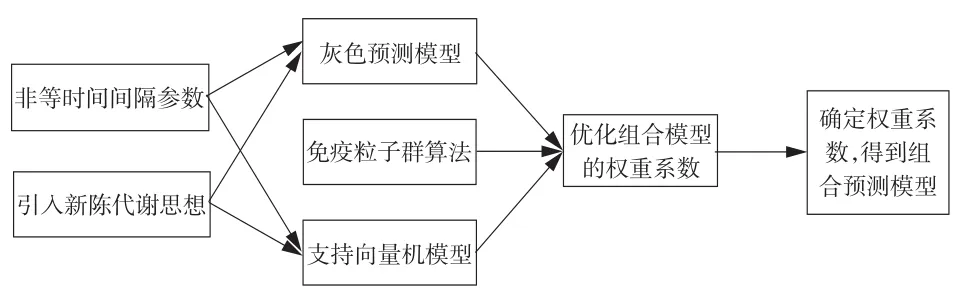
圖2 基于免疫粒子群優(yōu)化的組合預測模型Fig.2 Combined prediction model based on particle swarm optimization with immunity

4 仿真實例與分析

為驗證灰色預測模型和支持向量機方法對實際非等時間間隔性能綜合指數(shù)的預測能力，將圖1得到的性能指數(shù)按非等時間間隔選取(上述性能指數(shù)近似為等時間間隔)。選取時刻為[1、15、30、46、78、99、121、136、148、190、212、300、310、325、340、350、360、385、400、425、440、450、469、480、490、520、535、554、570、593]的發(fā)動機性能指數(shù)。其中，以[1、15、30、46、78、99、121、136、148、190、212、300、310、325、340、350、360、385、400、425]時刻對應的性能指數(shù)建立灰色模型和支持向量機模型，剩余時刻數(shù)據(jù)用于驗證模型，如圖3所示。

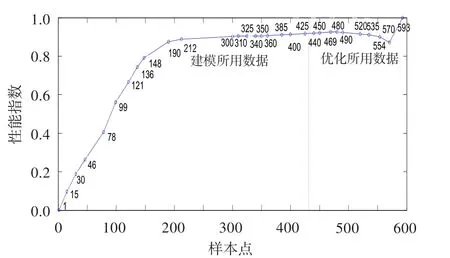
圖3 非等間隔數(shù)據(jù)Fig.3 Unequal-interval data

兩種預測模型均采用新陳代謝更新信息的思想進行預測。支持向量機模型的嵌入維數(shù)為8。在此基礎上，以免疫粒子群算法優(yōu)化組合模型的權重系數(shù)確定組合模型。其中，優(yōu)化算法中學習因子設置為1.4，慣性權重為0.5，替換概率為0.6，初始種群數(shù)為100，最大迭代次數(shù)為200，每隔10次檢測最優(yōu)個體是否變優(yōu)。

三種模型的預測結果如表1所示，可見，組合模型的預測精度明顯高于灰色預測模型，略高于支持向量機模型。以3.3節(jié)的免疫粒子群算法優(yōu)化其權重系數(shù)，得到灰色模型、支持向量機在組合預測模型中的權重系數(shù)分別為0.223 586和0.776 414。

三種模型預測的相對誤差如圖4所示。可見，除在個別點外，組合模型在絕大多數(shù)點處的預測精度都較優(yōu)，并且在469點和480點處的預測值極其接近真實值，大多數(shù)點處的預測誤差變化非常平緩。可以說，組合模型對短期預測具有很好的精度。

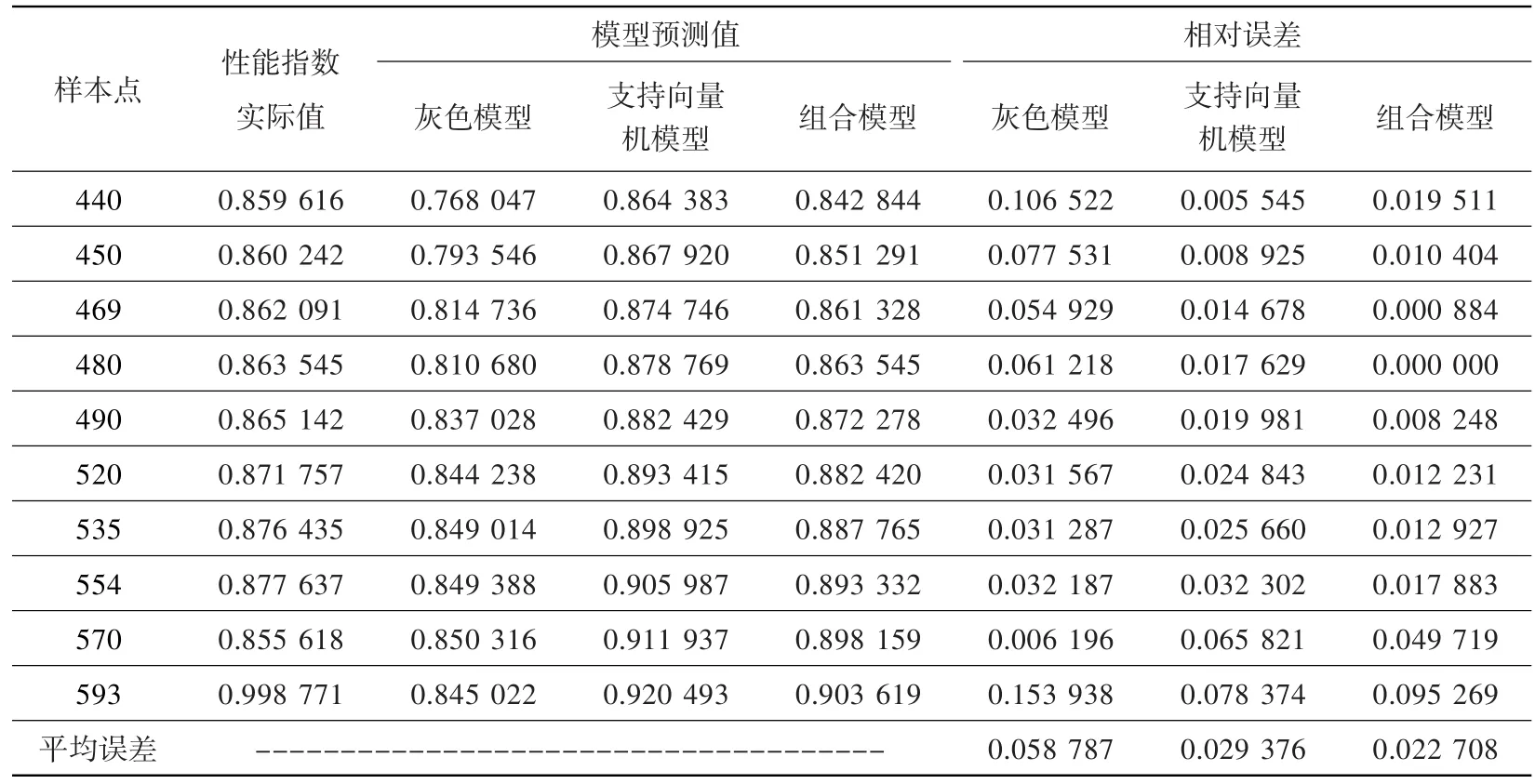
表1 結果對比Table 1 Comparison of results

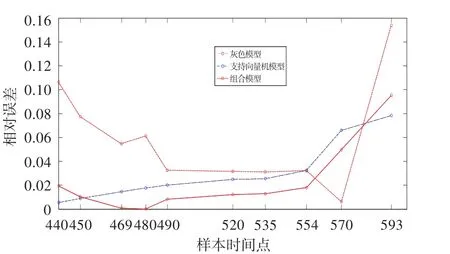
圖4 三種模型預測的相對誤差Fig.4 Predicting relative error of three models

5 結束語

本文以性能指數(shù)評估發(fā)動機性能狀況，并針對實際中性能指數(shù)一般為非等間隔、非線性的特點，利用兩種效果較好的預測模型(灰色模型和支持向量機模型)，以免疫粒子群算法優(yōu)化組合模型的權重系數(shù)，結合兩個模型的各自優(yōu)點，較好地預測了短期的發(fā)動機性能指數(shù)變化。利用不同模型組合開展中長期預測，將是下一步研究的重點。

[1]謝壽生.某型飛機發(fā)動機故障診斷與性能趨勢監(jiān)測研究[D].西安：西北工業(yè)大學，1998.

[2]胡金海，謝壽生.基于遺傳算法的發(fā)動機性能監(jiān)控與故障診斷[J].推進技術，2003，24(3)：198—200.

[3]胡金海，謝壽生，胡劍鋒，等.基于粗糙集理論的航空發(fā)動機性能綜合評判[J].系統(tǒng)工程與電子技術，2006，28 (5)：704—707.

[4]任淑紅，左洪福.基于性能衰退的航空發(fā)動機剩余壽命組合預測方法[J].機械科學與技術，2011，30(1)：23—29.

[5]Ming Liang，Boutros T.Mechanical Fault Detection Using Fuzzy Index Fusion[J].International Journal of Machine Tools and Manufacture，2007，47(11)：1702—1714.

[6]何慶飛，陳桂明，陳小虎，等.基于改進灰色預測模型的液壓泵壽命預測[J].潤滑與密封，2011，36(7)：27—31.

[7]張志警，劉潔瑜，馬學文.基于非等間距灰色模型的捷聯(lián)慣組誤差系數(shù)建模預測[J].導彈與航天運載技術，2011，5：40—42.

[8]呂永樂，郎榮玲，路輝，等.航空發(fā)動機性能參數(shù)聯(lián)合RBFPN和FAR預測[J].北京航空航天大學學報，2010，36(2)：131—134.

Combined Prediction Research of Unequal-Interval Engine Performance Synthetical Index Based on Particle Swarm Optimization with Immunity

LI Dong1，MA Li2，F(xiàn)AN Zhao-yuan2，SONG Yan1
(1.Graduate Student Brigade，Naval Aeronautical and Astronautical University，Yantai 264001，China；2.Engine Military Representatives Office of Navy in Shenyang，Liaoning 110015，China；3.Department of Fundamental Experiment，Naval Aeronautical and Astronautical University，Yantai 264001，China)

Firstly the measured parameters were filtered by Singular Value Decomposition Filtering Algo?rithm,and engine performance index was synthesized.Aimed at the problem of different interval for perfor?mance synthetical index,metabolism was introduced in improved gray predicting model,and a performance index predicting method of improved gray model and support vector machine(SVM)combination based on particle swarm optimization with immunity was presented.Simulating example indicates that the predicting precision of this method is more superior to improved gray model,better than SVM.But predicting result change of combined model is more stable for most sample points.

unequal-interval；engine performance synthetical index；improved gray model；support vector machine；particle swarm optimization with immunity；combination prediction

V235.13

A

1672-2620(2013)02-0042-04

2012-06-13；

2013-04-03

國家自然科學基金青年基金(61102167)

李冬(1984-)，男，遼寧葫蘆島市人，博士研究生，主要從事航空發(fā)動機性能衰退及評估預測研究。