線路截斷法在卷煙配送路徑規劃中的應用

魏 嫄， 曾 華， 吳耀華 WEI Yuan,ZENG Hua,WU Yao-hua

（1.山東大學 現代物流研究中心，山東 濟南 250061；2.四川省煙草公司成都市公司，四川 成都 610072）

在我國，一般以市級煙草配送中心為中心，直接配送到全市各地的上萬個配送點。負責卷煙配送的車輛由煙草配送中心出發，依次到其負責的收貨點進行配送，最終配送完成后車輛返回配送中心[1]。現有的卷煙配送車輛型號眾多，載貨量也有區別。卷煙配送路線的規劃是一個LS-VRP（大規模車輛路徑）問題，是一個NP問題。對于一般的LS-VRP問題有精確算法、亞啟發式算法和啟發式算法等。

眾所周知，我國卷煙配送工作由來已久，因此各地煙草商業企業在發展中已經形成了自己的配貨順序，并根據配貨順序安排配送車輛。這種配貨順序有其存在的合理性，并且已經在運行之中，進行較大的改動有一定的風險。但是傳統的車輛配送任務分配主要采取人工的方式進行，工作量大且優化程度較低。另外，在解決大規模VRP問題的方法中，一種思想先按照TSP問題利用算法生成一個全局的配送路線，之后對這個總的配送路線進行截斷，來確定分配給每輛車的配送路線，從而生成卷煙配送VRP問題的配送方案。這種方法優化程度較高，而且可以保證較快的計算速度。因此基于大線路截斷成小線路進行配送的方法有一定的實際價值。

而且除了總配送路程最短、費用最小、時間最短等一般VRP問題的約束之外，處于管理上的考慮，卷煙配送過程有其特有的特點，例如要求不同車輛工作時間比較均衡且小于上限、車輛之間的配送量均衡等。因此引入了一些原則進行配送任務劃分來保證車輛工作強度的均衡。

本文研究的基于配送任務均衡的線路截斷方法，屬于一種亞啟發式算法，主要實現的功能是在收貨點配送排序確定的情況下，把這些收貨點的配送任務分配給各配送貨車。貨車從配送中心出發，按照指定的順序配送其負責的收貨點，之后返回配送中心。在這個過程中要考慮配送路徑最短、所用車輛最少、配送工作量均衡的要求。

1 模型建立

收貨點配送任務序列為：

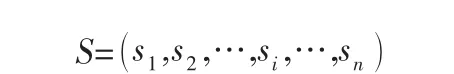
其中s1,s2,…,sn表示n個收貨點的收貨量。而其角標表示該收貨點配送的次序。s1為第一個配送，s2為第二個配送，依次類推，sn為最后一個。每個收貨點只能由一個車輛配送。

每個車輛包含標準載貨量和標準服務客戶數兩個指標，這兩個指標由車輛的型號和配送人員的工作時間確定。

配送車輛標準載貨量為：與標準載貨量、服務客戶數與標準服務客戶數的比值，即裝載率和服務率，用來衡量車輛的工作負荷程度。表示了所有車輛的裝載率和服務率。Pv與Pc計算了車輛實際裝載率、服務率與平均值的差值之和，其值越大表示車輛的任務分配越不均衡。目標函數反映了實際卷煙配送中的實際要求。

2 模型求解

在實際的配送過程中，首先需要設定每輛車的裝載率和服務率的上下限值即車輛的裝載率不得高

式中Dis表示每個配送車輛的配送距離d之和，即總配送距離。N為使用的車輛總數。ρvj、ρcj分別表示第j輛車的裝載量行配送任務的劃分。

為了保證任務量的均衡和較短的配送距離，本文設計了基于線路截斷的亞啟發式算法進行配送任務劃分。算法的流程如下：

Step1 對每輛車進行模擬裝車，以車輛j為例，將待分配任務序列（第一次循環時即為初始S序列）中的收貨點從前到后依次裝入車輛j中，當車輛j的裝載量與服務率之一達到其下限值時，當前最后一個裝入的點即為其裝載任務的下限點，假設該點為sl，之后繼續裝載，當車輛j的裝載量與服務率之一達到上限值時，最后一個裝入的點即為其裝載任務的上限點，假設該點為su，則車輛j的可截斷區間為［sl,su］。即該車輛的當前配送任務可以是從配送序列的第一個點s1開始到［sl,su］中任何一點結束。計算所有車輛的可截斷區間。

Step2 找到每個車輛可截斷區間內相隔距離最長的一組相鄰點兩點之間距離記錄為Savj， 則車輛的模擬配送任務為是剩余配送任務序列的起始點，即新的s1。之后比較所有車輛當前模擬裝車的使用效率選擇使用效率最高的車型作為當前循環的所選車型，其配送任務為其對應的 （s1… sa），將已配送的點以及該車輛從任務序列和備選車型中刪除。于其上限值，也不能低于其下限值，服務率亦然。這樣可以保證車輛的使用率。如果車輛運力緊張的情況下可以將下限值提高，但會降低在配送距離優化中的調整余地。如果需主要考慮配送里程的節約可以適當擴大區間，從而可以在更寬的范圍內進

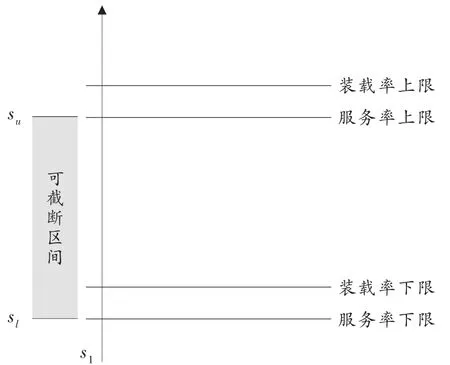
圖1 某車輛的服務區間計算示意圖

Step3 如果最后一個車的使用效率低于平均使用效率的20%，則可以通過調高每輛車的裝載率和服務率下限值之后返回Step1，直到將最后一輛車的配送任務分配至其他車輛為止。如果使用效率高于平均使用效率的20%低于85%，則通過調低每輛車的裝載率和服務效率下限值返回Step1，可以減少前面車輛的任務量，提升最后一輛車使用效率。如果最后一輛車的使用效率高于平均使用效率的85%則任務分配結束。

若循環20次之后仍無法跳出循環，則輸出當前解。

3 仿真實驗與數據分析

下面通過Matlab軟件編程進行仿真實驗。

配送任務序列為某地市實際卷煙配送任務，共712個點。

輸入數據：

配送中心與收貨點、各收貨點之間的距離矩陣，各收貨點的收貨量，車輛矩陣：

車輛編號 1 2 3 4 5 6 7 8 9載貨量下限 3 800 3 800.0 3 800.0 4 200.0 4 800.0 5 000.0 5 500 5 800.0 6 000.0載貨量上限 4 180 4 180.0 4 180.0 4 620.0 5 280.0 5 500.0 6 050 6 380.0 6 600.0服務客戶數下限 70 75.0 75.0 75.0 75.0 75.0 80 85.0 85.0服務客戶數上限 77 82.5 82.5 82.5 82.5 82.5 88 93.5 93.5

首次循環的裝車方案為：

車輛編號 3 1 2 4 5 6 7 8 9載重量 3 623.00 3 881.00 4 163.00 4 169.000 4 493.00 5 368.00 4 839.00 5 246.00 2 498.00服務客戶數 82.00 77.00 79.00 82.000 82.00 82.00 88.00 93.00 47.00裝載率 0.95 1.02 1.09 0.992 0.93 1.07 0.87 0.90 0.41服務率 1.09 1.10 1.05 1.090 1.09 1.09 1.10 1.09 0.55

當前總配送里程為1 262km。由于最后一輛車的使用效率0.96為平均使用效率2.06的46%，從而通過調低其他車輛的載貨量與服務率的下限來將前面的車配送任務向后移。

通過8次循環調整后，裝車方案為：

車輛編號 4 7 8 9 5 1 3 6 2載重量 3 575.00 4 489.00 4 361.00 4 899.00 5 033.00 3 822.00 4 013.00 4 239.00 3 849.00服務客戶數 81.00 87.00 92.00 92.00 80.00 58.00 77.00 81.00 64.00裝載率 0.85 0.81 0.75 0.81 1.04 1.00 1.05 0.84 1.01服務率 1.08 1.08 1.08 1.08 1.06 0.82 1.02 1.08 0.85

當前總配送里程為1 201km。最后一輛車的使用效率1.96為平均使用效率1.93的1.014%，達到終止條件，配送任務分配完畢。整個算法運行時間為1.87s。

可以看出，該算法可以在很短的時間內完成大規模配送任務的劃分，并且較好地實現了配送任務的均衡與配送里程的節約，從而可以針對不同的卷煙需求做出相應的配送方案，從而實現動態任務規劃和卷煙敏捷供應的目的。

[1] 翁建紅，李朝陽.基于GPS的煙草物流配送線路規劃[J].物流科技，2008,31(9):18-20.