高瞬態響應指標的伺服系統設計方法

周 文，李長紅，韓耀鵬，楊執中，藺 韜，張匯博

(西北機電工程研究所，陜西 咸陽 712099)

在20 世紀50 年代后期聯邦德國西門子公司提出了調節器的最佳整定設計方法［1-2］，更多的伺服系統采用與最佳整定設計方法相近的伺服系統經典設計方法［3-5］，經典設計方法通過小時間常數處理，將多個小時間常數的慣性環節，將每個小時間常數求和，用這個時間常數和確定一個慣性環節，并用這個慣性環節代替多個慣性環節，然后按照典型Ⅰ型與Ⅱ型系統的不同設計準則設計伺服系統。伺服系統在很多領域都有廣泛的研究應用［6-11］，隨著工業，制造業，武器裝備等對伺服系統越來越高的要求，設計出高瞬態響應指標的伺服系統，是伺服系統設計追求的目標之一。為了設計出高瞬態響應指標的伺服系統，針對經典設計方法中的缺陷進行改進，提出了采用比例微分單元實現零極點對消，對消掉較大時間常數的極點，然后按照典型Ⅰ型與Ⅱ型系統的設計準則設計系統的調節器。這種設計方法克服了經典設計方法中小時間常數處理引入的誤差，由于對消掉較大時間常數的慣性環節，設計中引入的誤差小，使伺服系統設計更準確，同時設計的伺服系統具有較大的帶寬，因此提高了伺服系統的瞬態響應指標。

1 設計數據及要求

為了更好的說明本文方法能夠設計出高瞬態響應指標的伺服系統，采用大多數文獻較常用的例子［2，5］。例:某晶閘管供電的雙閉環直流調速系統，采用三相橋式整流電路，數據如下:

直流電動機:220 V、136 A、1 460 r/min，反電勢系數Ce=0.132 Vmin/r，允許過載倍數λ=1.5。

晶閘管裝置放大系數:Ks=40。

電樞回路總電阻:R=0.5 Ω。

時間常數:Tl=0.03 s，Tm=0.18 s。

電流反饋系數:β=0.05 V/A。

轉速反饋系數:α=0.007 Vmin/r。

采用三相橋式整流電路的平均失控時間Ts=0.001 7 s，電流濾波時間常數Toi=0.002 s，轉速濾波時間常數Ton=0.01 s。

設計要求:電流回路要求超調量σ≤5%，轉速、位置無靜差。

2 伺服系統的經典設計方法

2.1 電流環設計

經典設計方法［2］，在設計中按小時間常數處理，取TΣi=Ts+Toi=0.003 7 s，采用Ⅰ型系統設計，采用PI 調節器，選擇PI 調節器參數，使其對消掉控制對象的大時間常數極點，即τi=Tl，其中τi是PI 調節器的時間常數。設計要求超調量σ≤5%，可取阻尼系數等于0.707，KITΣi=0.5，其中KI是電流環開環放大倍數。可計算KI=1/2TΣi=1/(2 ×0.003 7)=135.1，從而可得電流環PI 調節器為

其中，Ki是電流環PI 調節器的放大倍數，Ki=KITlR/Ksβ=1.013。因此電流環的閉環傳遞函數為

2.2 轉速環設計

在轉速環設計時，將電流環及式(2)等效為式(3)的慣性單元

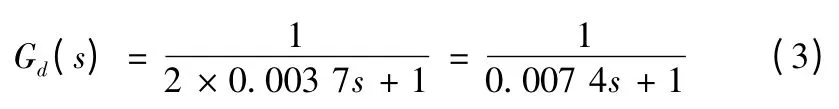
轉速環設計，按小時間常數處理，取T∑n=2T∑i+Ton+Toi=0.0174 s，采用II 型系統設計，采用PI 調節器，設計的Ⅱ型系統轉速環，按照最小閉環幅頻特性峰值準則設計，根據抗擾和跟隨性能都較好的原則，選取h=5，超前時間常數τn=hTΣn=5 ×0.0194 =0.097 s，則轉速環開環增益為

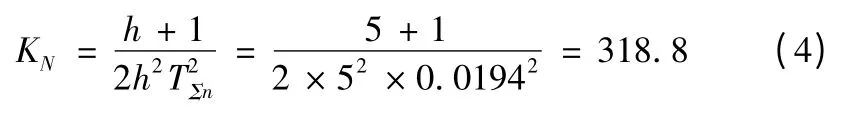
則轉速環PI 調節器的增益為Kn=10.5，對應的PI 調節器為

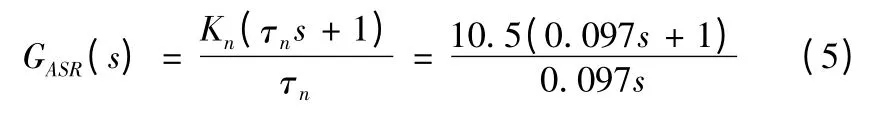
因此轉速環的閉環傳遞函數為

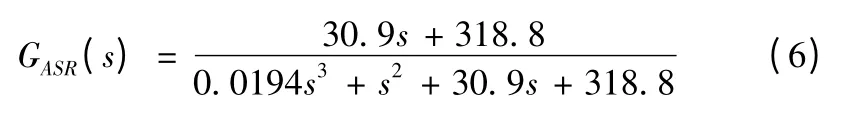
2.3 位置環設計

在位置環設計時，將轉速環及式(6)等效為式(7)的慣性單元位置環設計，按小時間常數處理，取T∑p= 0. 025 + Ton=0.035 s，采用Ⅱ型系統設計，采用PI 調節器，設計的II 型系統位置環，按照最大相角裕度準則設計，選取h=5，超前時間常數τp=hTΣp=5 ×0.035 =0.175 s，則位置環PI 調節器的增益為Kp=0.09，對應的PI 調節器為

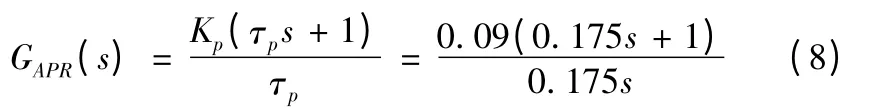
3 伺服系統設計

經典方法小時間常數處理，在幅度和相位上存在很大的誤差，如圖1。圖1 是將整流電路的平均失控時間環節與電流濾波環節進行小時間常數處理前后的幅頻特性曲線的對比。標有“TΣi”是進行小時間常數處理后的幅頻特性曲線，標有“Ts，Toi”是小時間常數處理前的幅頻特性曲線。相位和幅度在低頻段十分接近，但在高頻部分存在很大誤差，因此很有必要引入更精確的設計方。

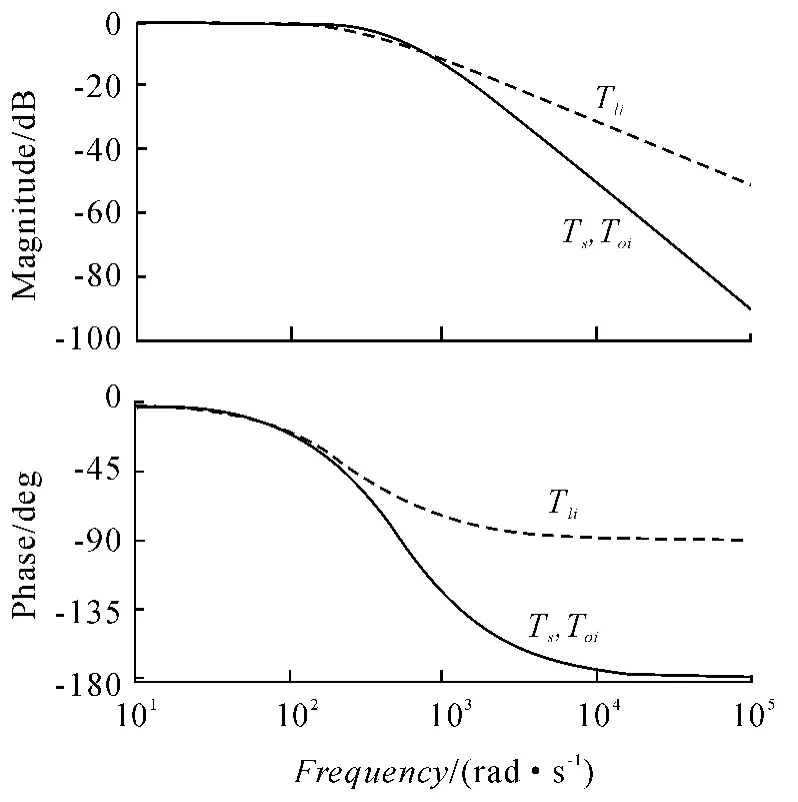
圖1 按小時間常數處理前后的幅頻特性曲線

3.1 電流環設計

為了減小在設計中引入的誤差，電流環在設計時，不進行小時間常數處理，而是按照電流環自身特性進行處理，采用PID 調節器，用PID 調節器的微分環節進行零點和極點對消。具體設計如下:

采用Ⅰ型系統設計，PID 調節器為

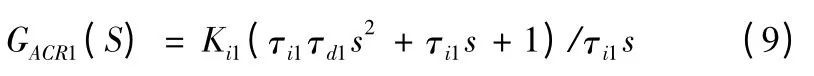
選擇PID 調節器參數，使其對消掉控制對象的大時間常數極點，即

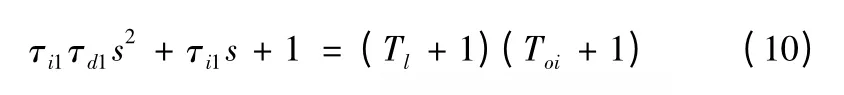
可得τi1=0.032，τd1=0.001 875。設計要求超調量σ≤5%，可取阻尼系數等于0.707，KITs=0.5，因此電流環開環放大倍數為

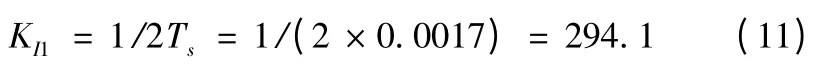
可得到PID 調節器放大倍數Ki1=2.35 則對應的電流環PID調節器為

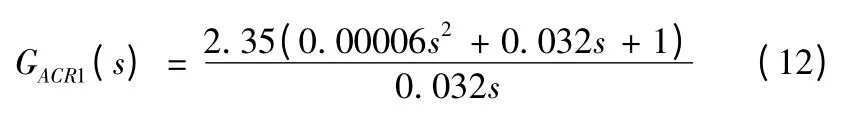
對應電流環的閉環傳遞函數為

與電流環閉環傳遞函數近似等效的傳遞函數為

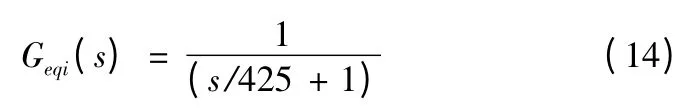
其中425 是閉環傳遞函數高頻段斜率線與0 dB 軸交點對應的頻率。

3.2 轉速環設計

轉速環就可以按照圖2 進行設計。

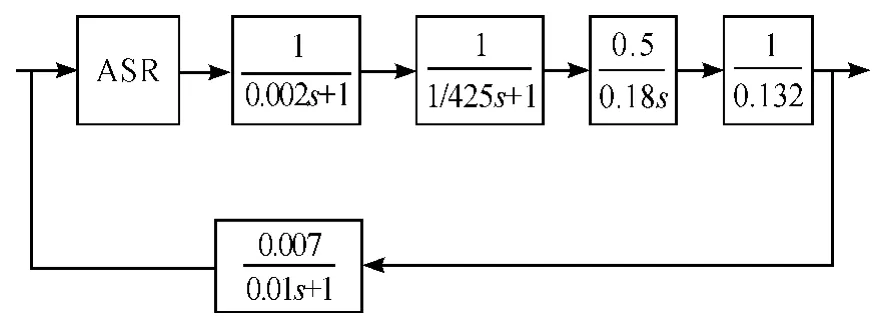
圖2 電流環等效后的轉速環框圖

轉速環采用Ⅱ型系統，用2 個PD 調節器對消掉最大的2 個慣性環節，然后采用PI 調節器進行校正。轉速環較大的慣性環節為濾波環節，因此PD 調節器為

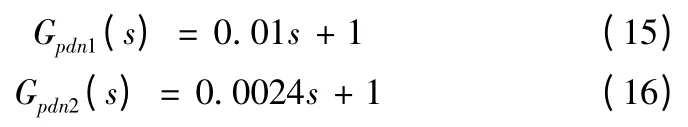
式(15)、(16)2 個PD 調節器對消掉2 個慣性環節。接下來設計PI 調節器，轉速環PI 調節器的形式為

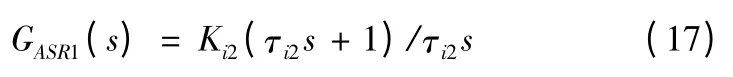
按照典型II 型系統最小閉環幅頻特性峰值準則，根據抗擾和跟隨性能都較好的原則，選取h=5，則τi2=5 ×0.002 =0.01 s，因此轉速環開環增益為

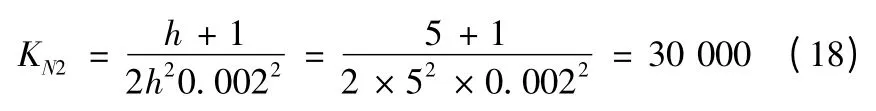
可計算出轉速環調節器增益為Ki2=101.8，則轉速環調節器為

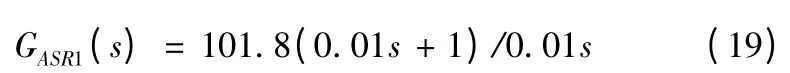
對應轉速環的閉環傳遞函數為

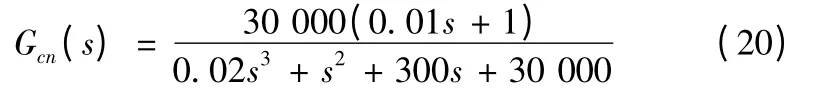
與轉速環閉環傳遞函數近似等效的傳遞函數為

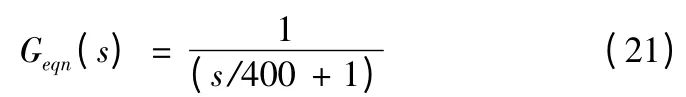
其中400 是閉環傳遞函數高頻段斜率線與0 dB 軸交點對應的頻率。

3.3 位置環設計

位置環采用Ⅱ型系統，用一個PD 調節器對消掉時間常數最大的一個慣性環節，然后采用PI 調節器進行校正。位置環較大的慣性環節為濾波環節，因此PD 調節器為

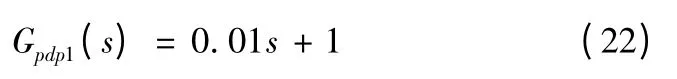
PD 調節器對消掉時間常數最大的慣性環節。接下來設計PI 調節器，位置環PI 調節器的形式為

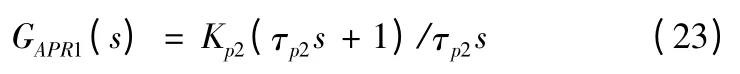
按照典型Ⅱ型系統最大相角裕度設計準則，選取h =5，則τp2=5 ×0.0025 =0.012 5 s，可計算出位置環調節器增益為Ki2=0.25，則轉速環調節器為

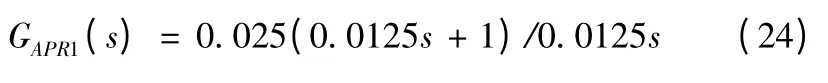
4 2 種方法的實驗仿真

4.1 2 種方法的系統框圖

經典方法與本文方法得到的系統框圖如圖3、圖4。圖3、圖4 是經過調試后的結果，圖3 只對轉速環的時間進行調整，由原來的0.097 調為0.4，這時階躍響應效果較好;圖4僅對位置環的時間進行調整，由原來的0.25 調為0.44，這時階躍響應效果較好。

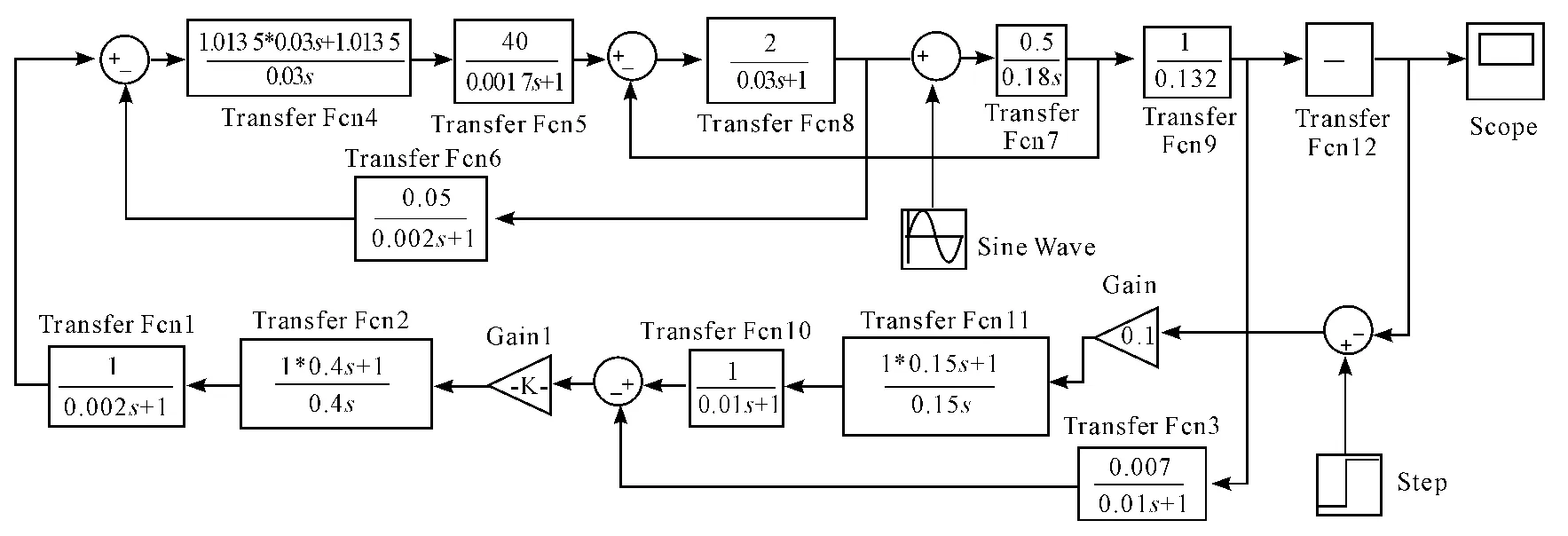
圖3 經典方法系統圖

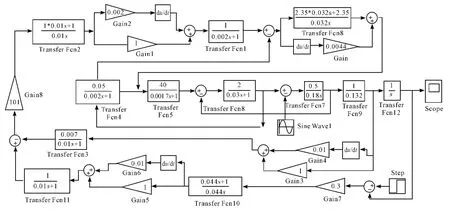
圖4 本文方法系統圖

4.2 2 種方法結果對比

由于本文提出的方法對消掉較大時間常數的慣性環節，設計的控制系統帶寬較寬，因此設計的控制系統比經典方法的瞬態響應更好。為了比較說明，經典方法和本文方法都加階躍信號，階躍時間0.1 s。經典方法和本文方法的階躍響應如圖5 和圖6。

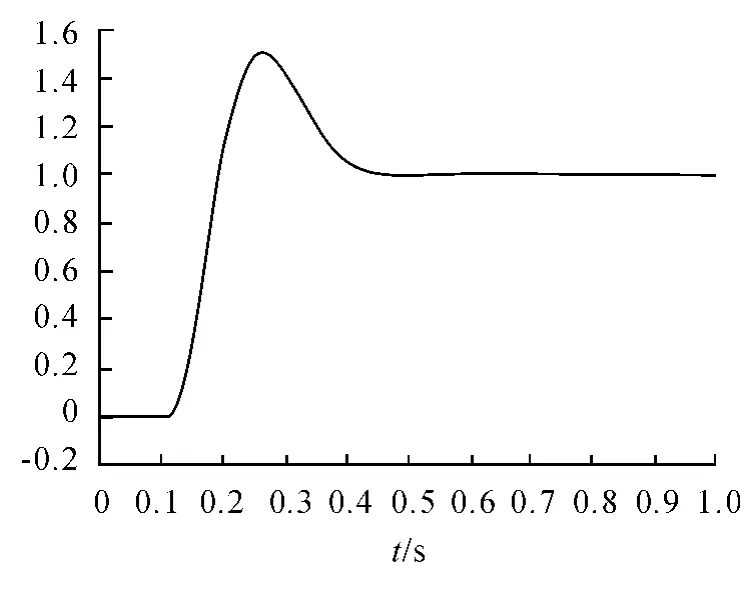
圖5 經典方法階躍響應

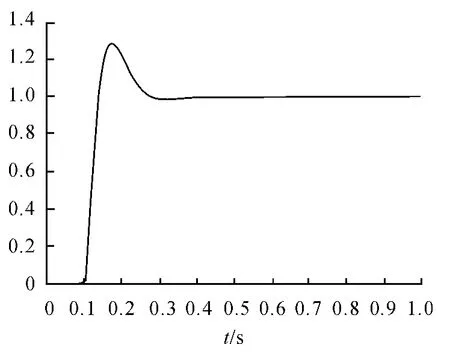
圖6 本文方法階躍響應

為了比較2 種方法的階躍響應結果，將各種指標列于表1。

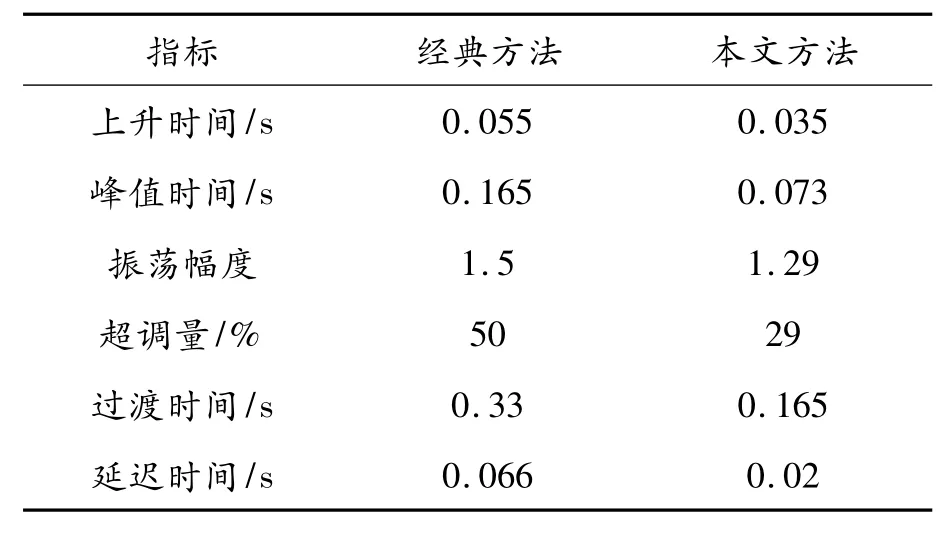
表1 瞬態響應指標

從表1 很明顯看出本文方法的各項瞬態響應指標都優于經典方法。其中最主要的過渡時間和超調量2 個指標都很好，不僅超調量小而且過渡時間快，這樣優越的指標很符合現代工業，制造業，武器裝備等對伺服系統高瞬態響應指標的要求。

以上比較了2 種方法的瞬態響應指標，接下來再看2 種方法的位置環開環傳遞函數幅頻特性。幅頻特性的繪制參考［12］的方法。經典方法的位置開環傳遞函數的幅頻特性曲線如圖7。本文方法的位置開環傳遞函數的幅頻特性曲線如圖8。

為了更好比較2 種方法的幅頻特性，將幅頻特性圖反映的指標寫于表2 內，具體數據見表2。

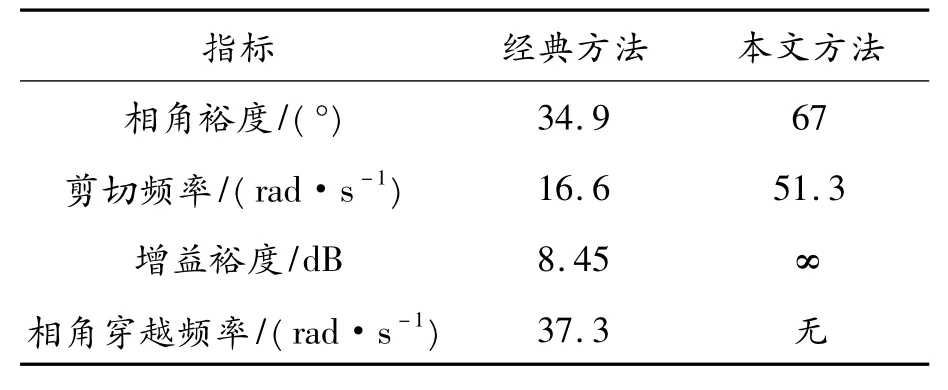
表2 幅頻特性指標

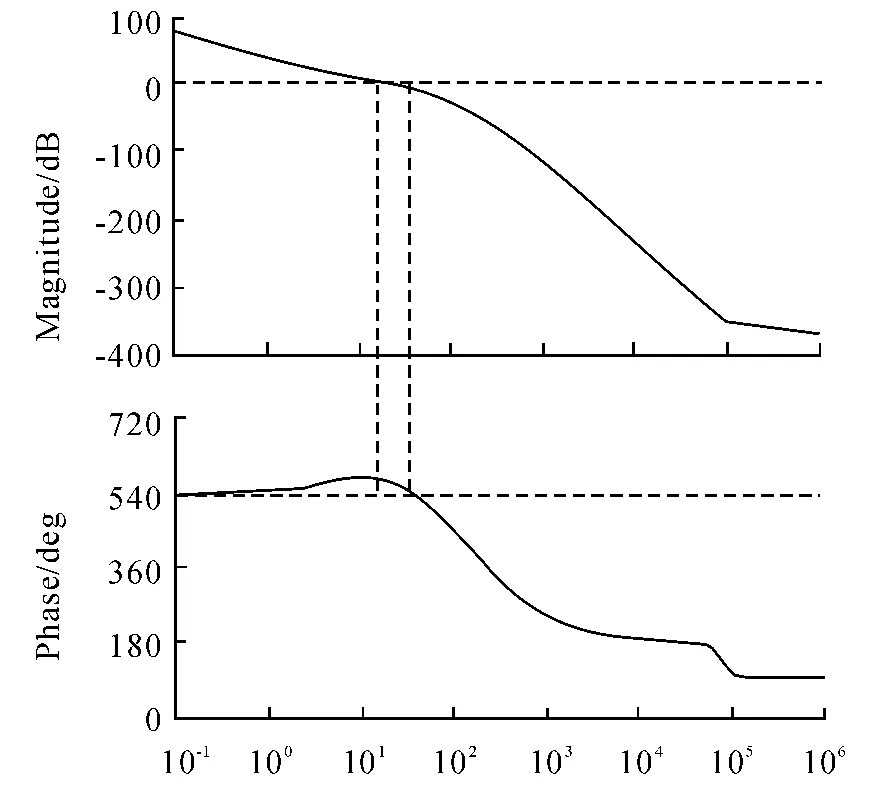
圖7 經典方法位置開環傳遞函數幅頻特性圖

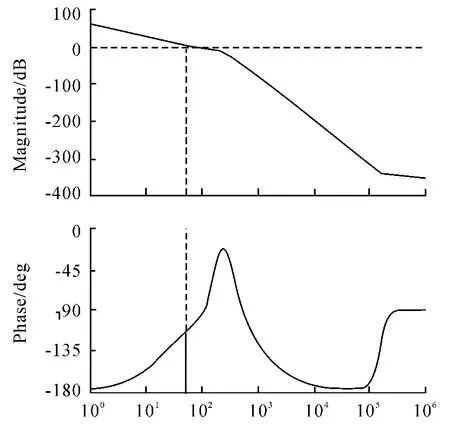
圖8 本文方法位置開環傳遞函數幅頻特性圖

從表2 中看出經典方法的相角裕度為34.9°，本文方法的相角裕度為67°，本文方法的相角裕度是經典方法的2 倍，這說明本文方法得到的控制系統比經典方法得到的控制系統有更高的穩定裕度。經典方法的剪切頻率為16.6 rad/s，本文方法的剪切頻率為51.3 rad/s，本文方法的剪切頻率是經典方法的3 倍，這說明本文方法得到的控制系統具有更大的帶寬。本文方法得到的增益裕度和相角穿越頻率也明顯優于經典方法。這些指標說明本文方法得到的控制系統具有更高的瞬態響應指標。

從階躍響應指標和幅頻特性曲線反映的指標比較可以看出，本文的設計方法，設計的伺服系統不僅動態性能好而且穩定可靠。

5 結束語

通過對同一個設計任務用經典設計方法和本文提出的設計方法進行設計。與經典方法設計的控制系統相比，本文方法設計的控制系統具有更高的瞬態響應指標，更高的穩定裕度。本文設計方法的缺點是需要增加比例微分環節，在一定程度上增加了系統的成本。比較可以看出在一些對瞬態響應要求高的伺服控制系統中，本文的設計方法具有明顯的優越性。

［1］陸道政，季新寶.自動控制原理及設計［M］.上海:上海科學技術出版社，1978.

［2］陳伯時.電力拖動自動控制系統［M］.北京: 機械工業出版社，1999.

［3］張莉松，胡祐德，徐立新.伺服系統原理與設計［M］.北京:機械工業出版社，2008.

［4］顏嘉男，王自強.伺服電機應用技術［M］.北京:科學出版社，2010.

［5］杜繼宏，王詩宓.控制工程基礎［M］.北京:清華大學出版社，2008.

［6］李長春，孟亞東，劉曉東，等.電液伺服系統的同步控制研究［J］.兵工學報，2007，28（6）:765-768.

［7］Cheng G Y，Peng K M. Robust composite nonlinear feedback control with application to a servo positioning system［J］.IEEE Transactions on Industrial Electronics，2007，54（2）:132-140.

［8］Lin F，Lin C.A permanent-magnet synchronous motor servo drive using self-constructing fuzzy neural network controller［J］.IEEE Trans on Energy Conversion，2004，19（1）:751-759.

［9］Tal J.Design and analysis of pulse width modul-ated amplifiers for DC servo systems［J］.IEEE Trans.on IECI，2004，23（1）:23-28.

［10］Ramesh R，Mannan M A，Poo A N.Tracking and contour error control in CNC servo systems［J］.International Journal of Machine Tools and Manu-facture，2005，45（3）: 301-326.

［11］Yao J J，Wang L Q，Jing H Z，et al.Adaptive feed—forward compensator for harmonic cancellation in an electro-hydraulic servo system［J］. Chinese Journal of Mechanical Engineering，2008，21（1）:77-81.

［12］黃忠霖.自動控制原理的MATLAB 實現［M］.北京:國防工業出版社，2007.