基于遺傳算法的彈道優化算法

張樂蓉，宋 龍，章惠君

(中國空空導彈研究院，河南 洛陽 471009)

空空導彈彈道優化研究的目的是提高導彈的飛行性能，達到精確、有效的攔截目標。導彈彈道優化問題已成為現代導彈技術的重點發展方向之一，很多學者在彈道優化方面做了大量研究。文獻［1］利用序列二次規劃法對導彈縱向彈道整體進行優化，文獻［2］通過非線性規劃的直接方法優化得到最優的初始彈道等。

但在彈道優化問題中大多數解決方法是數值優化的方法，數值優化本質是根據初始條件，終端約束，指標函數可得到特征彈道，即飛行彈道的基本幾何形狀，故采用一般數值的方法進行優化在很大程度上受初始條件的約束和影響，尤其是當目標有多個極值點時［1］。而遺傳算法是一種模擬物種生存進化體制的搜索算法，它并不依賴于問題本身，通過對種群方向性的選擇、交叉和復制操作來完成搜索，同時又具有魯棒性、隱含并行性等的特點，因而該算法成功的運用于許多復雜優化問題的求解。針對空空導彈的數學模型，對給定的模型及氣動參數，將彈道傾角作為控制變量，采用遺傳算法優化采樣點數據求得優化彈道方案。與比例導引方案彈道相比，在相同時間和相同射程的情況下，遺傳算法優化彈道的末端速度較大，具有一定優越性。

1 導彈模型

1.1 導彈模型

不考慮地球自轉影響，導彈在鉛錘平面內運動的質心運動方程組為

其中m 為導彈質量，P 為發動機推力，X 為阻力，θ 為彈道傾角，Y 為升力，ms 為導彈質量變化率，α 為攻角，V 為導彈速度。

阻力模型:

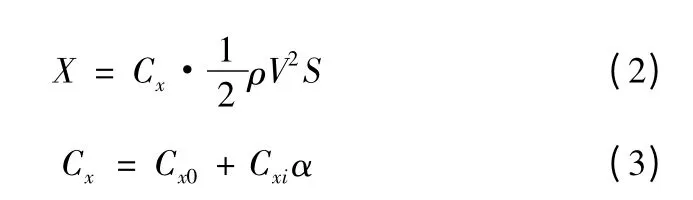
式(3)中，Cx0為零升阻力系數;Cxi為誘導阻力系數。

大氣密度模型:

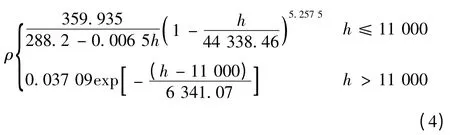
推力模型為:

式(5)中，Tmax為發動機所能提供的最大推力;k 為常系數，k∈［0，1］。

1.2 問題描述

本文以末端速度最大值作為性能指標

初始投放條件

由上可知目標問題為:從已知初始狀態(x0，y0，v0)，要求轉移到末端時刻t=tf時，脫靶量r≤25 m，v(tf)達到最大。

當導彈模型以及氣動力參數都給定時，在給定時間，給定距離的情況下，假定導彈小攻角飛行，則應存在一組優化的彈道傾角，使得導彈能以最大末速度擊中目標。而本文就通過尋找這一組優化的彈道傾角從而得到末端速度最大的優化彈道。

2 遺傳算法

彈道優化是一種復雜的非線性的多約束(多為隱性約束)問題，現有的傳統優化方法均屬于局部優化方法，如果目標問題存在多個極值點，通過傳統方法是很難得到最優解，因而采用傳統優化方法進行彈道優化存在一定的局限性。

遺傳算法是一種模擬生物種群進化過程的搜索方法，通過基因編碼和種群進化講復雜的問題簡單化，在遺傳進化過程中尋找到最優解。遺傳算法優化的重點在于基因的編碼方式與適應度函數的選取，對優化問題的具體細節要求并不高，因而具有很強的魯棒性。其尋優是有指導而非盲目的進行搜索，迭代產生的新一代個體總是優越于上一代個體，全局搜索的同時隱含并行性，多點同時進行搜索，使得尋優效率更高。這些優點使得遺傳算法對導彈的彈道優化這個復雜的非線性優化問題具有一定的優越性。

3 優化算法設計

3.1 遺傳算法方案

3.1.1 編碼方案

按照遺傳算法優化的設計思想，建立目標優化問題和基因結構之間的關系式遺傳算法的關鍵，即確定算法的編碼方式以及解碼運算。常用的編碼方式有兩種:二進制編碼與浮點數編碼。二進制編碼采用固定長度的二進制符號串來表示群體中的個體，其等位基因由{0，1}構成;而所謂浮點數編碼則是指個體的每個基因用某一范圍內的一個浮點數來表示，這種編碼方式直接使用變量的真實值，故不需要解碼操作［6］。文中優化的變量為彈道傾角，范圍為［0，pi/2］，因而采用二進制編碼方式即可滿足需求。

3.1.2 基本遺傳操作

在遺傳算法的進化過程中，起到最關鍵作用的是選擇、交叉和變異操作。因而產生了3 個最基本的遺傳操作算子:選擇算子、交叉算子和變異算子。通過這3 個算子對進化過程隨即性的操作，使得群體在進行n 代后更接近最優解，其接近程度與3 種算子采取的操作形式緊密相關。

1)選擇算子。選擇算子，也叫做復制算子，它以適應度作為評價的基準，將上一代優秀的個體基因復制遺傳到下一代，產生新的群體，使得個體向最優解逐漸靠攏。選擇算子是遺傳進化過程中的重要環節，其好壞直接影響到算法的優劣。

目前現有的選擇算子主要有輪盤賭選擇、隨機競爭選擇、最佳保留選擇、確定性選擇和無回放隨機選擇等。

本文采用了最佳保留選擇，利用“排名”的思想，從種群眾隨機的選取K 個個體，然后將這K 個個體按照適應度值得大小進行排序，找出K 個個體中的最優個體，遺傳到下一代。

2)交叉算子。在優化過程中，種群是通過基因的交叉操作產生新的個體，從而保證種群的多樣性，擴大優化進程尋優的范圍。交叉算子直接決定了算法是否收斂，是遺傳優化算法的核心操作。

常用的交叉算子有單點交叉、兩點交叉、均勻交叉以及算術交叉等。文中采用了兩點交叉，使得遺傳算法的尋優范圍更廣搜索能力更強。

3)變異算子。變異操作是模仿生物遺傳進化過程中出現的基因突變現象，某些基因位發生突變，產生新的個體，引進變異操作的目的是為了保證種群的多樣性，同時使得遺傳算法也有了一定的隨機搜索能力，防止算法出現早熟收斂。

常見的變異算子有基本位變異、有效基因突變、概率自調整突變、均勻突變以及非均勻突變等。文中采用的是均勻突變，即每一個基因位都以相同概率變動。

3.1.3 適應度函數的選取

適應度是遺傳算法用來衡量個體好壞的標準，是尋優過程的評價機制。在每次迭代產生的群體中，適應度高的個體更容易進入下一代，而適應度低的個體進入下一代的幾率則相對較低。描述適應度大小的函數則成為適應度函數，指導著遺傳優化過程的方向。

文中討論的導彈最優控制問題以最大末端速度為性能指標，因此這里以末端速度值作為適應度函數。

3.2 算法流程

選用上面介紹的二進制編碼方案，選擇、交叉和變異算子以及適應度函數構成求解導彈最優化問題的遺傳算法，算法流程如圖1 所示。

圖1 遺傳算法設計流程

4 優化算例

給定導彈初始高度為5 000 m，初始速度為300 m/s，目標初始位置為(30 000，5 000)，并以100 m/s 的速度水平向右運動。性能指標是末端速度最大。其他仿真參數如下:

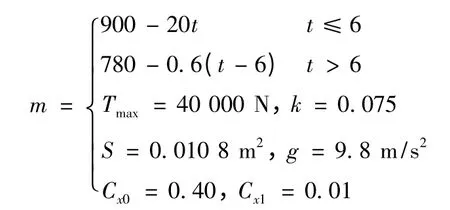
遺傳算法種群大小取100，精英個體數目為20，最大迭代次數為100，種群個體范圍為［-1.57，1.57］。

利用如上參數采用比例導引仿真得到的彈道，彈道射程為40 km，其末端速度為698.2 m/s，飛行時間為97 s，脫靶量為0。按照根據圖1 所示算法，選取20 組采樣點數據作為優化變量，利用遺傳算法進行計算，在進化100 代后得到了相同飛行時間、射程下的末速度最大彈道，優化得到的彈道的末端速度為730.95 m/s，脫靶量為0.024 0，相比比例導引末端速度是它的1.05 倍。兩種方案均用97 s 的飛行時間在(40 000，5 000)點處擊中目標，其彈道傾角隨時間變化曲線、速度隨時間變化曲線以及彈道曲線如圖2 ～4 所示。

圖2 導彈速度隨時間變化曲線

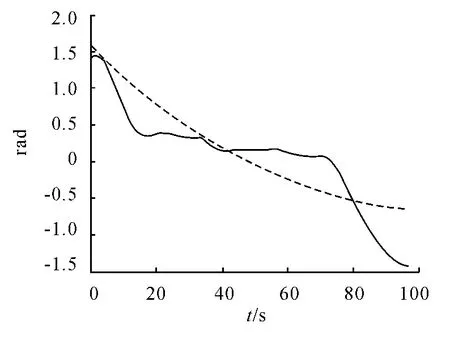
圖3 彈道傾角隨時間變化曲線

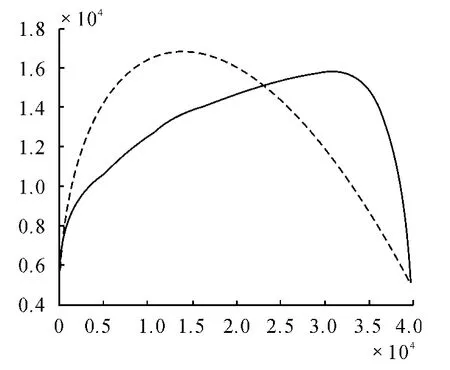
圖4 導彈軌跡曲線

5 結束語

遺傳算法優化飛行方案先斜向上飛行，然后在下滑段減小導彈軌跡與重力方向的夾角，利用重力和推力的作用來增加優化彈道末段速度，這種飛行方案在同等飛行時間、同等射程情況下，得到的末端速度遠大于比例導引飛行方案得到的末端速度。通過比較比例導引方案與遺傳優化方案的仿真結果，可以發現基于遺傳算法的優化飛行方案在彈道優化方面有一定優越性，為空空導彈標準彈道的設計提供了一種參考。

［1］趙昕，艾飛.地理約束下遠程滑翔導彈彈道優化［J］.戰術導彈技，2010，6:8-12.

［2］陳羅婧，劉莉，于劍橋.三點法導引導彈初始段弧形彈道優化設計及實現［J］.彈道學報，2009，6:65-69.

［3］熊西軍.基于遺傳算法的超遠程制導火箭彈彈道優化設計［D］.成都:電子科技大學，2009.

［4］耿麗娜，鄭志強.基于遺傳算法的制導炸彈最優控制律［J］. 中 南 大 學 學 報: 自 然 科 學 版，2007，38（1）: 176-181.

［5］鮮勇，許立軍.遺傳算法在導彈飛行程序設計中的應用研究［J］.系統仿真學報，2009，21（5）:1502-1504.

［6］肖偉.遺傳算法的研究及其在倒立擺中的應用［D］.長沙:中南大學，2011.