基于改進人工魚群算法的配電網電容器優化投切

黃 奇 丁曉群

（河海大學能源與電氣學院，江蘇南京 210098）

并聯電容器是配電網無功補償的重要設備，根據不同的負荷水平來進行電容器的投切，可以達到降低網絡損耗，改善電壓分布，提高系統安全系數的效果。近年來，電力系統的諧波污染日趨嚴重[1]。因此，為了避免電容器投切過程中出現的諧波放大或諧振現象[2,3]，在限制電容器投切次數的同時還必須考慮到諧波問題對電容器投切的影響[4]。

配電網電容器優化投切的基本模型主要有靜態優化[5,6]和動態優化[7]兩種，本文采用的是計及投切代價的配電網電容器優化投切模型。這種模型在目標函數中以計及投切代價的方式來處理電容器投切次數的限制，避免將投切次數的限制作為一個約束條件，從而使優化方案既能具備靜態優化計算簡單的優點，又能有效地控制電容器的投切次數。此外，本文模型中還考慮到了諧波的影響，以電網中各節點的電壓總諧波畸變率（THD）為約束條件，保證優化方案中系統各節點的THD不超過規定的限值，避免諧波放大。

針對本文的優化模型，提出了基于改進人工魚群算法[8,9]的求解方法。由于基本人工魚群算法在收斂速度和搜索精度上的不足，引入了遺傳算法中的交叉、變異思想[10]對其進行改進。最后通過對IEEE 9節點系統進行仿真，表明了該算法較其他一些算法的優越性。

1 數學模型

電容器的優化投切是一個多變量、多約束條件的非線性規劃問題。本文選取的控制變量為可投切電容器的投入組數，以電能損耗的費用和投切代價費用之和最小為目標函數來建立優化模型，考慮的約束條件有基波和諧波潮流約束、電容器的投入組數約束、電壓上下限約束以及THD限值約束。

1.1 目標函數

式中，PL為系統的總網損；T為總的優化時間，一般為1h；KE為電能損耗費用的系數；?qj為節點j處電容器投入組數的變化量；Kq為電容器進行一次投切動作的代價系數；NC為裝有可投切電容器的節點數目。

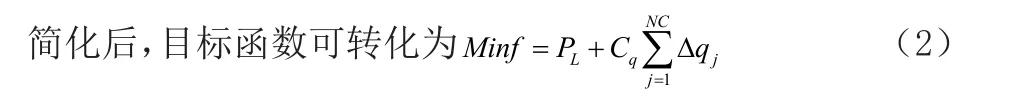
式中，Cq為以功率形式表示的投切代價系數，單位為kW/次。

1.2 約束條件

1.2.1 等式約束

其中，式（3）為基波潮流約束，式（4）為各次諧波潮流約束，X,q分別為系統的狀態變量和控制變量，Ik為k次諧波電流向量，Vk為k次諧波電壓向量，Yk為k次諧波導納矩陣，h為所研究諧波的最高次數。

1.2.2 不等式約束

其中，式（5）為電容器的投入組數約束，式（6）為電壓上下限約束，式（7）為THD限值約束。qj和qj,max分別為節點j處電容器投入的組數和安裝的組數和分別為節點j處基波電壓有效值和k次諧波電壓有效值，Vmax和Vmin分別為節點電壓的上下限值，THDj和THDmax分別為節點j處的電壓總諧波畸變率和最大限值。

2 人工魚群算法

人工魚群算法（AFSA）是2002年由李曉磊等人提出的一種隨機優化算法，它是一種模擬魚群覓食游弋行為的新型算法。它的全局搜索能力良好，且對初值、參數選擇不敏感，還有魯棒性強、簡單、易操作等優點。其算法的流程圖如下：

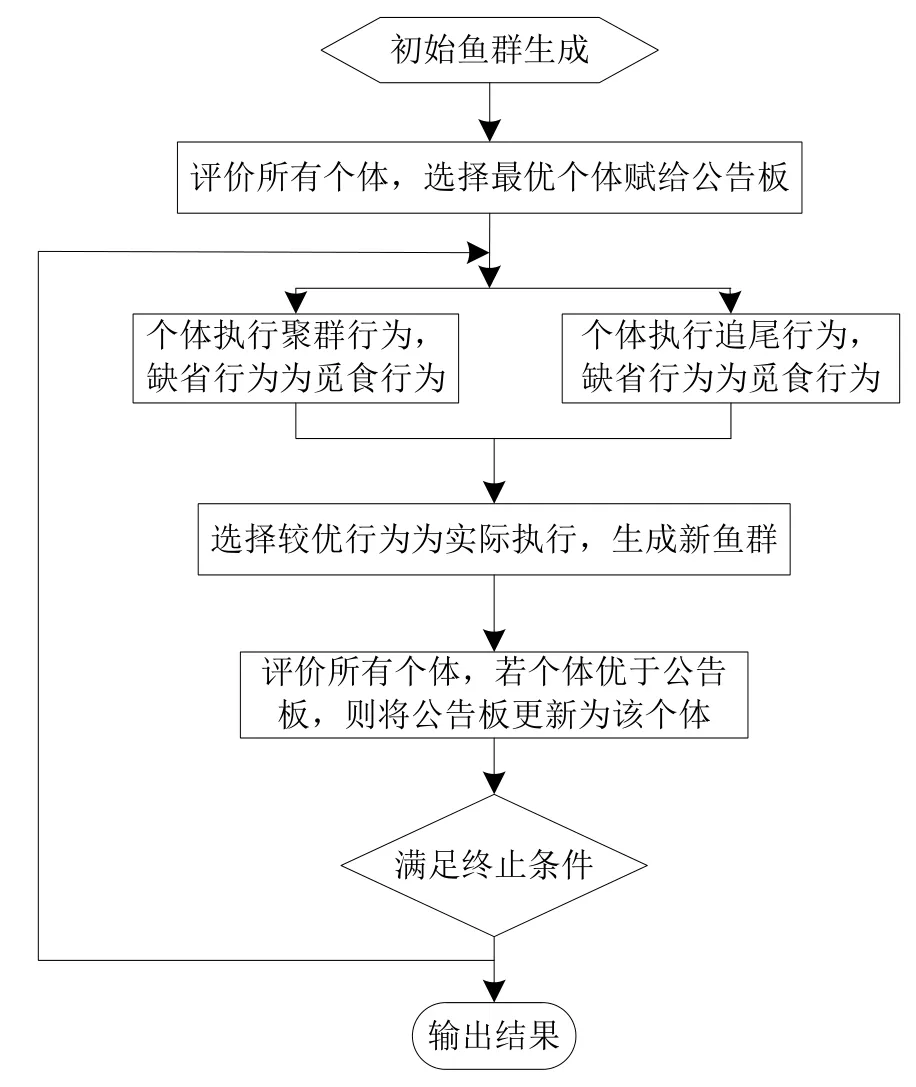
圖1 人工魚群算法流程圖

3 改進人工魚群算法

當人工魚個體處于漫無目的的隨機移動狀態或當大量人工魚聚集在非全局極值點的時候，算法的收斂速度將大大減慢，搜索精度也將大大降低。為了克服這個缺點，特此引入了遺傳算法中的交叉、變異算子。當公告板在連續幾個迭代過程中都沒有發生變化或變化極小時，保留此最優狀態，將其它人工魚個體按一定的概率進行交叉、變異操作。該算法的設計如下：

3.1 生成初始魚群：設置人工魚的感知范圍Visual，最大移動步長Step，擁擠度因子δ，每次覓食最大試探次數Trynumber。將初始公告板在連續幾個迭代過程都沒有發生變化或變化極小時的迭代次數Beststep←0，初始的迭代次數Num←0，在可行的控制變量區域內隨機生成N條人工魚個體，構成初始魚群。

3.2 將公告板賦初值：計算各初始人工魚個體當前所處狀態的函數值Y，取Y值最優的賦予公告板上。

3.3 進行行為選擇：各人工魚個體分別模擬聚群行為和追尾行為，選取Y值較優的行為進行，缺省方式為覓食行為。并且各人工魚每次行為進行完畢之后，都要將自身狀態的函數值Y與公告板上的作比較，若優于公告板上的值，則以自身取代之，并將Beststep置為0。

3.4 判斷是否引入交叉、變異算法：判斷Beststep是否已經達到了預設的公告板連續不變化或變化極小次數的最大閾值Maxbest，若是，轉到第5步執行；否則執行第6步操作。

3.5 引入交叉、變異算法：對除公告板上最優人工魚個體外其他的所有人工魚進行以下操作：

3.5.1 交叉操作：以交叉概率Pc從人工魚群中隨機選擇兩條人工魚進行交叉操作，形成兩條新的人工魚個體。將這兩條新人工魚個體的Y值分別與公告板上的值作比較，若優于公告板，則以自身取代之，并將新的人工魚個體取代舊個體。

3.5.2 變異操作：以變異概率Pm從人工魚群中隨機產生新個體，并初始化該個體。然后計算各新人工魚個體所處狀態的函數值Y，并將它與公告板上的值作比較，若優于公告板，則以自身取代之。

3.5.3 將Beststep置為0。

3.6 判斷算法是否終止：判斷最優解是否已經在滿意的誤差界限內或者Num是否已經達到了預設的最大迭代次數Maxnumber，若不是，則Num←Num+1，Beststep←Beststep+1，繼續執行第3步操作；否則執行第7步操作。

3.7 算法終止，輸出公告板上的最優解。

通過引入遺傳算法中的交叉、變異算子，使魚群中人工魚個體產生了跳變，從而調整優化了群體。不僅使AFSA的收斂速度得到提高，同時其全局的搜索能力也得到了保證。

4 算例分析

本文應用上述改進人工魚群算法對IEEE 9節點系統進行仿真計算。模型和算法中主要參數設置如下：人工魚群規模N=50，最大移動步長Step=0.5，感知范圍Visual=15，最大試探次數Trynumber=20，擁擠度因子δ=0.618，最大不變化次數Maxbest=10，最大迭代次數Maxnumber=50,交叉概率cP=0.20，變異概率Pm=0.05；投切代價系數Cq=4kW/次，各點的電壓限值為Vmin=0.85，Vmax=1.05，maxTHD=6%；諧波最高次數為5次。

該算例系統的接線圖見文獻[3]，電容器配置見表1。表2為不同優化方法下的結果比較。

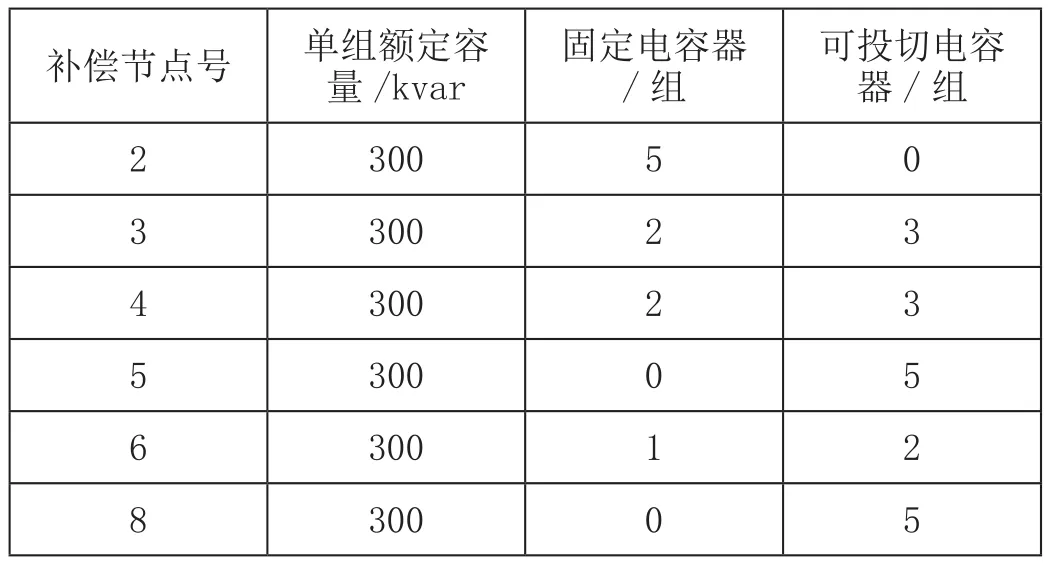
表1 IEEE 9節點配電系統的電容器配置

表2 不同優化方法下結果比較

由上面表2可以看出：①與優化前相比，本文算法在有效控制電容器投切次數和各節點THD值的情況下，可降低網損60.89kW，降幅達11.71%；②較基本人工魚群算法，本文算法在網損下降量與優化后最低電壓上均有所提高；③較遺傳算法，本文算法雖然在優化后最低電壓上稍低，但差別并不顯著，而網損下降量確有明顯提高，提高了2.33%。

5 結論

本文在計及投切代價的配電網電容器優化投切模型的基礎上考慮了諧波的影響，針對本文的優化模型，提出了基于改進人工魚群算法的求解方法。經過算例仿真分析，本文方法有以下幾個特點：

5.1 本文在配電網電容器優化投切模型的約束條件中加入了THD限值的約束，避免了優化方案中各節點出現的諧波放大問題，保證了系統的安全。

5.2 本文首次將人工魚群算法應用到配電網電容器的優化投切中，并針對算法后期收斂速度大大減慢、搜索精度大大降低的缺點，結合遺傳算法的思想對其進行改進。改進后的算法明顯優于原來的算法。

[1]田友元.電力系統并聯電容器運行的諧波問題[J].電力電容器,1999,2:1－7.

[2]Huang Z, Xu W, Dinavahi V R.A Practical Harmonic Resonance Guideline for Shunt Capacitor Applications[J].IEEE Trans.on Power Delivery,2003,18(4): 1382－1387.

[3]Yu X, Xiong X, Wu Y.A PSO-based Approach to Optimal Capacitor Placement with Harmonic Distortion Consideration[J].Electric Power Systems Research,2004,71(1): 27－33.

[4]婁素華,吳耀武,余欣梅,等.考慮諧波影響的配電網電容器優化投切研究[J].水電能源科學,2008,26(4):187－190.

[5]Hsu Y Y, Kuo H C.Dispatch of Capacitors on Distribution System Using Dynamic Programming[J].IEE Proceedings Part C,1993,140(6):433－438.

[6]吳文傳,張伯明.電容器實時優化投切的最優匹配注入流法[J].中國電機工程學報,2004,24(1):35－39.

[7]Deng Y, Ren X, Zhao C, et al.A heuristic and Algorithmic Combined Approach for Reactive Power Optimization with Time-varying Load Demand in Distribution Systems[J].IEEE Trans.on Power Systems,2002,17(4):1068－1072.

[8]劉白,周永權.基于遺傳算法的人工魚群優化算法[J].計算機工程與設計,2008,29(22):5827－5829.

[9]鄭華,劉偉,張粒子,等.基于改進人工魚群算法的電網可用傳輸能力計算[J].電網技術,2008,32(10):84－88.

[10]張愛軍,馮煜珵,陳陳,等.基于改進遺傳算法的電容器優化配置[J].寧夏電力,2006,3:1－5.