多學科設計優化方法在燃氣輪機設計中的應用

楊子龍，王志強

（1．中國艦船研究院，北京 100192；2. 中國船舶重工集團公司第七O三研究所，哈爾濱150036）

0 引言

隨著科學技術日新月異的發展，燃氣輪機設計的要求日益提高，其復雜程度已遠超乎常人想象。設計不僅需要大量的人力，而且還牽涉到數十門學科。傳統設計方法需要不斷往復于各相對獨立的“學科孤島”之間進行分析計算，設計人員工作量大，產品開發周期長。多學科設計優化(Multidisciplinary Design Optimization，MDO)方法極大的縮短了結構設計周期，降低了設計人員的工作強度，并保證了設計前后燃氣輪機的各項指標得到提高。

目前，多學科設計優化是基于確定性條件的優化過程，沒有考慮產品設計的不確定因素。由于沒有考慮這種不確定性因素的影響，使得最優設計通常接近約束的邊界，沒有給不確定因素留夠空間。當設計變量由于不確定性發生波動時，最優解將會在約束邊界附近變化，有可能落入失效區域。因此，為了保證設計結果可靠性，需要在設計時考慮到可靠性，基于可靠性的多學科優化(Reliability Based Multidisciplinary Design Optimization，RBMDO)正是這樣一種設計方法[1-6]。

本文針對傳統燃氣輪機設計周期長、設計可靠性低的問題，提出基于雙循環方法的典型燃氣輪機部件多學科可靠性優化設計方法；采用近似技術縮減設計計算規模，提高設計效率；以典型燃氣輪機渦輪葉片為例，實現了燃氣輪機部件基于可靠性的多學科優化設計，通過與確定性優化設計方法進行比較，驗證方法的有效性。

1 循環方法的多學科可靠性設計優化方法

RBMDO是用于改進或提高設計可靠性，或將失效概率降低到一個設定的上限以下的設計優化方法。其基本思想是：要求設計產品在滿足一定性能的條件下，使其可靠度達到最大；或者使設計產品達到最佳性能指標時，要求它的工作可靠度不低于某一規定水平。在工程問題中，后者的應用更為廣泛，本文的RBMDO也采用后者。

雙循環的優化迭代過程分為兩個部分，內部是可靠性分析循環，外部是優化循環，使含有可靠性約束的問題得到最優解。可靠性分析嵌套在優化循環中，每次優化迭代需執行多次可靠性分析計算每個概率約束和靈敏度，基于雙循環方法的RBMDO過程如圖1所示。

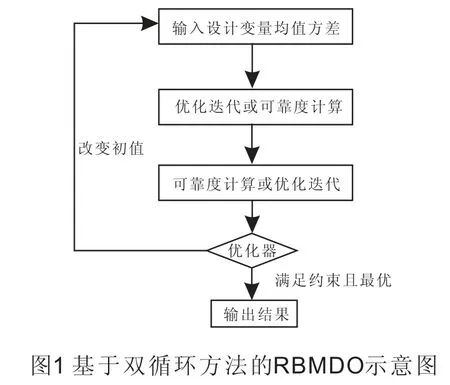
2 Kriging函數的近似模型

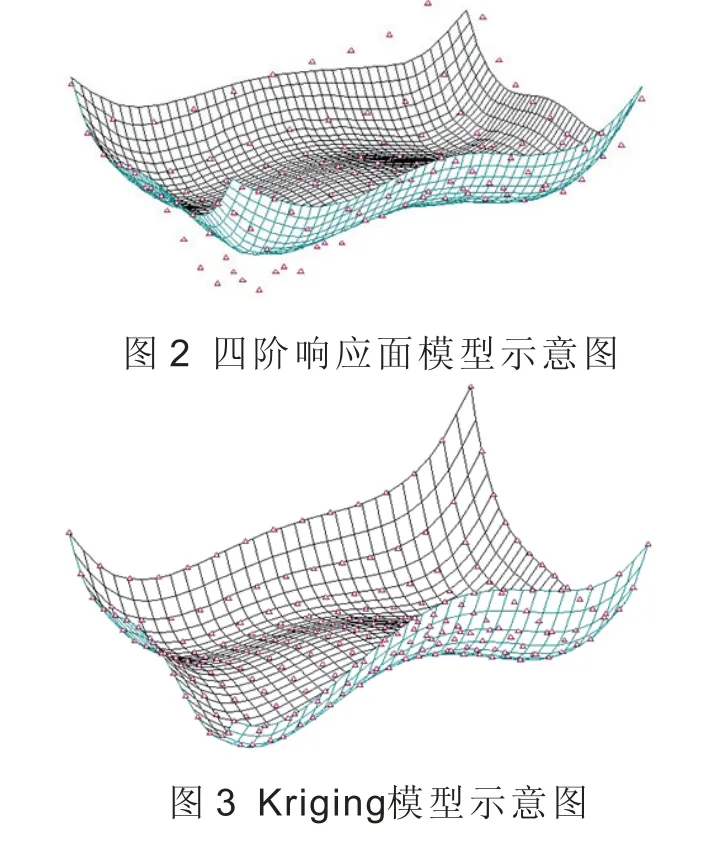
目前，工程應用中的近似模型多為多項式響應面模型。該模型多局限于設計空間的局部，同時對非線性程度較高的問題預測效果不夠理想。對于燃氣輪機RBMDO，涉及的學科和設計變量都比較多，設計空間也很復雜，因此在優化過程中需要使用全局近似模型策略，而Kriging模型正好適用于全局近似；另外，Kriging模型對高度非線性問題的預測效果也明顯好于多項式響應面模型。圖2、圖3為四階響應面模型和Kriging模型擬合精度對比，從圖中可以看到Kriging模型精度明顯高于四階響應面模型。

本文采用Kriging近似模型代替仿真程序進行設計目標尋優。優化流程包括：給定一組基準設計點，使用仿真程序對設計點進行多學科分析，并建立數據庫文件，這一過程可通過試驗設計完成；通過數據庫文件建立Kriging近似模型；使用近似模型在設計空間中進行搜索，得到近似問題的最優解；在最優解處調用仿真程序進行實際的多學科仿真分析；將仿真分析的結果加入數據庫文件，更新近似模型；重復，直至收斂。

3 基于可靠性的多學科設計優化技術在燃氣輪機設計中的應用

本文采用基于雙循環的RBMDO方法對以燃氣輪機典型渦輪葉片為例進行優化設計。以燃氣總壓損失Ploss為優化目標，以葉身最高溫度Tmax、葉身平均溫度Taver、葉尖最大位移dmax和葉身最大應力σmax為可靠性約束。設定需要達到的可靠度為0.95(β=1.645)。采用雷-菲法對最終優化結果進行可靠性分析。根據試驗設計建立優化目標和約束的 Kriging近似模型，通過多學科分析更新近似模型，提高精度。

優化模型：min Ploss

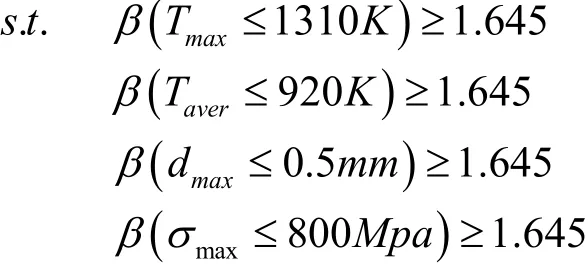
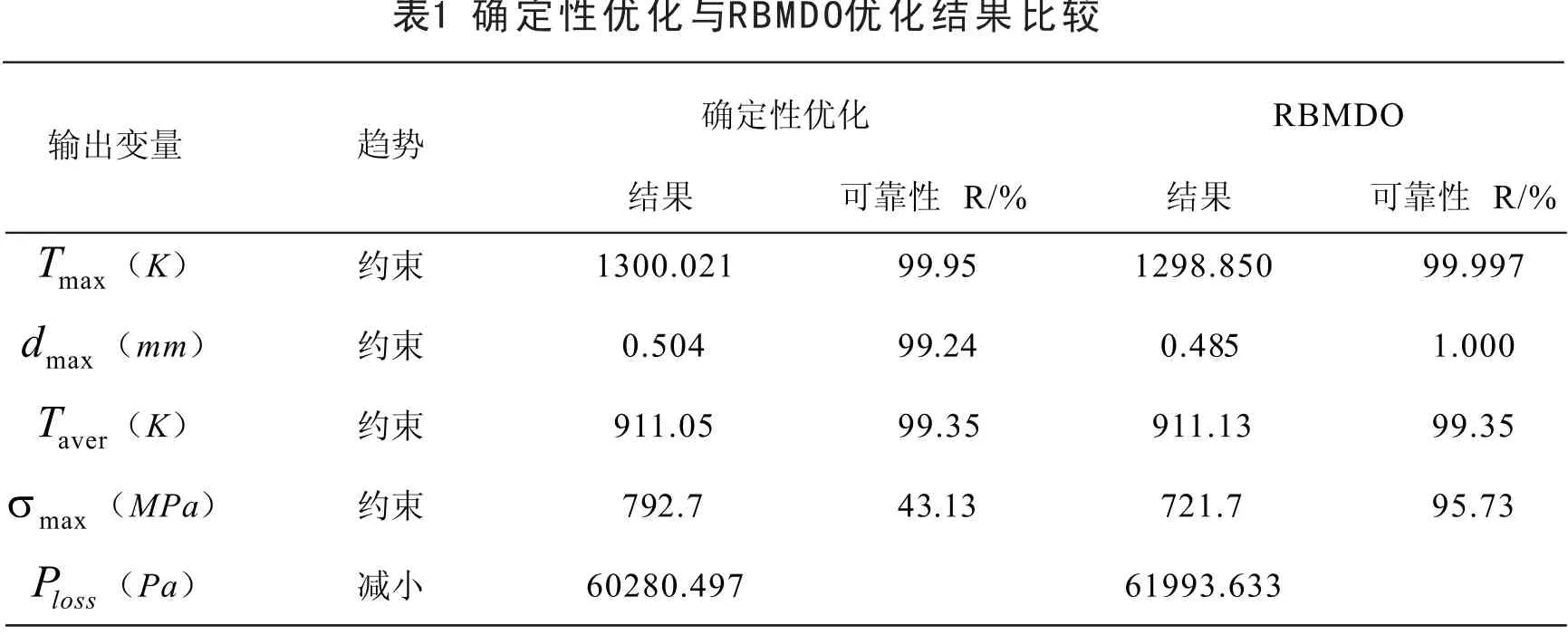
確定性優化與RBMDO結果如表1所示，結果表明，葉尖最大位移、葉身最高溫度和葉身平均溫度的可靠度達到了99.24% 、99.95%和99.35%，這樣的優化結果可以接受。但葉身最大應力的可靠度僅為43.13%，不能滿足工程應用要求。有必要進行基于可靠性多學科設計優化。

?

通過RBMDO，葉身最大應力的可靠度提高到了95.73%，優化結果滿足可靠性約束的要求。總壓損失與與確定性優化相比有所提高，這是由于考慮了不確定因素的影響，在優化過程中犧牲了部分性能以滿足可靠性的要求，這也說明RBMDO是一個折中過程，最終使結構性能和可靠性要求達到平衡。葉片經過RBMDO前后的葉尖及葉根截面型線見圖4。

4 結論

基于雙循環多學科可靠性優化設計方法實現了燃氣輪機典型渦輪葉片優化設計，提高了燃氣輪機典型部件的綜合性能；與確定性優化設計結果比較表明基于可靠性的多學科設計優化方法可以通過犧牲部分性能達到設計可靠性顯著提高；基于Kriging函數的近似模型可以顯著提高優化設計效率，縮短設計周期。

[1] Dhanesh Padmanabhan, Stephen M. Batill.Decomposition strategies for reliability based optimization in multidisciplinary system design[C].AIAA-2002-5471.

[2] Fan Hui, Li Weiji. An efficient method for reliability-based multidisciplinary design optimization[J]. Chinese Journal of Aeronautics. 2008,(22)： 335-340.

[3] Harish Agarwal, John E. Renaud. New decoupled framework for reliability-based design optimization[J]. AIAA Journal. 2006, 44(7)：1524-1531.

[4] Liping Wang, Srinivas Kodiyalam. An efficient method for probabilistic and robust design with non-normal distributions[C]. AIAA-2002-1754.

[5] Xiaoguan Chen, Timothy K. Hasselman. Douglas J.Neill. Reliability based structural design optimization for practical applications[C]. AIAA-97-1403.

[6] Joongki Ahn, Jaehun Lee, Suwhan Kim, Jang Hyuk Kwon. Sequential reliability analysis framework for multidisciplinary systems[C]. 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference 30 August -1 September. Albany： New York, 2004.