基于能量守恒平均電路的半橋變換器建模與仿真

張 慶，張小勇，孫立輝，謝 偉，周 帥

（株洲南車時代電氣股份有限公司，湖南株洲 412001）

0 引言

開關變換器，廣泛應用于通訊系統、電力電子系統中，是通訊電源、各類變流器的核心部分，特別是在電力電子系統中占有舉足輕重的地位。在電力電子應用領域，開關變換器性能的優劣，直接決定了所開發產品的質量。因此，對開關變換器的研究顯得極為重要。開關變換器的建模是研究開關變換器的拓撲結構和控制方法的基礎。開關變換器在工作中，由于功率開關管的開關作用，開關變換器的工作情況是周期性的時變結構系統。開關變換器的這一時變非線性周期性工作性質使得控制系統經典分析法無法直接應用。因此，近年來發展出了新的建模方法，用以解決開關變換器的建模問題[1-2]。

1 開關變換器建模方法

目前開關變換器的主要建模方法即平均法，平均法是把開關變換器一個周期內不同拓撲的電路，在某種意義下進行平均，將時變電路等效為非時變線性電路，從而利用經典的線性電路理論和控制理論來分析開關變換器的工作問題。

1.1 狀態空間平均法[3]

1976 年Middlebrook R.D.等提出了狀態空間平均法。以原始網絡的電容電壓、電感電流為狀態變量，按照變換器開關元件的“開通”和“關斷”兩種狀態，利用時間平均技術，得到一個工作周期內的平均狀態變量。從而將一個非線性、時變的開關電路等效為一個線性、時不變的連續電路。狀態空間平均法的基本公式如下：

其中：x 為電感電壓與電容電流的狀態變量；y為輸出狀態變量d為開關管的占空比；Vi為輸入電壓；A1，A2，B1，B2，C1，C2為與電路參數有關的系數矩陣。

其優點是，物理概念清晰，易于掌握；其缺點是，在分析包含較多元元件的電路時運算量巨大。

1.2 能量守恒平均電路法[4]

能量守恒平均電路法融合三端開關元件模型法、時間平均等效電路法、能量守恒法的基本思想，構建了考慮包括各元件寄生電阻在內的多種元件寄生參數的開關變換器建模方法。其基本思路為：

（1）將非理想元件等效為理想元件及其寄生參數的串聯，開關管等效為理想開關和開通電阻的串聯，二極管等效為理想開關、正向壓降、正向電阻的串聯等；

（2）根據能量守恒原理得到各類寄生電阻的等效值；

（3）將理想開關由整個周期的時間平均受控電壓源、電流源替代；

（4）將由（2）得到的寄生參數折算到輸出電感支路中；

（5）用占空比d 控制的理想變壓器取代受控電壓源、電流源，得到標準模型；

（6）基于標準化模型，推導出傳遞函數。

2 半橋DCDC變換器建模及其傳遞函數

2.1 半橋逆變全橋整流變換器建模

本文根據能量守恒平均電路法的基本思想，對半橋逆變全橋整流DCDC 變換器進行了建模。典型的半橋逆變全橋整流DCDC 變換器的電路原理如圖1 所示。其中S1、S2兩個開關管完全相同；D1、D2兩個快速回復二極管完全相同；D3～D6四個整流二極管完全相同；兩個輸入電容完全相同，共同分擔輸入電壓。

圖1 典型半橋DCDC變換器電路

將圖1 中的各類非理想元件等效為理想元件與寄生參數串聯之后（其中輸入電容的寄生電阻折算到Ron中，Lk為變壓器漏感），得到典型半橋逆變全橋整流DCDC 變換器的等效電路如圖2所示。

圖2 等效半橋DCDC變換器

圖3 考慮變壓器漏感時系統的時序圖

考慮到變壓器漏感的影響，系統工作的時序如圖3 所示。S1、S2為開關管的控制波形；iS為總輸入電流；i1為流過變壓器原邊的電流；iS1、iS2為流過開關管的電流；iD1～iD6為流過各個二極管的電流；考慮到輸出電感一般比較大，認為輸出電流近似不變，即iL=IL。

由于變壓器漏感會引起變壓器副邊繞組電壓的占空比丟失即圖3中時間t1的部分。占空比丟失D1為：

副邊有效占空比為：

由圖3 分別可以得到各瞬時值i1，iS，iS1，iD1，iD3，vs，vD3的表達式：

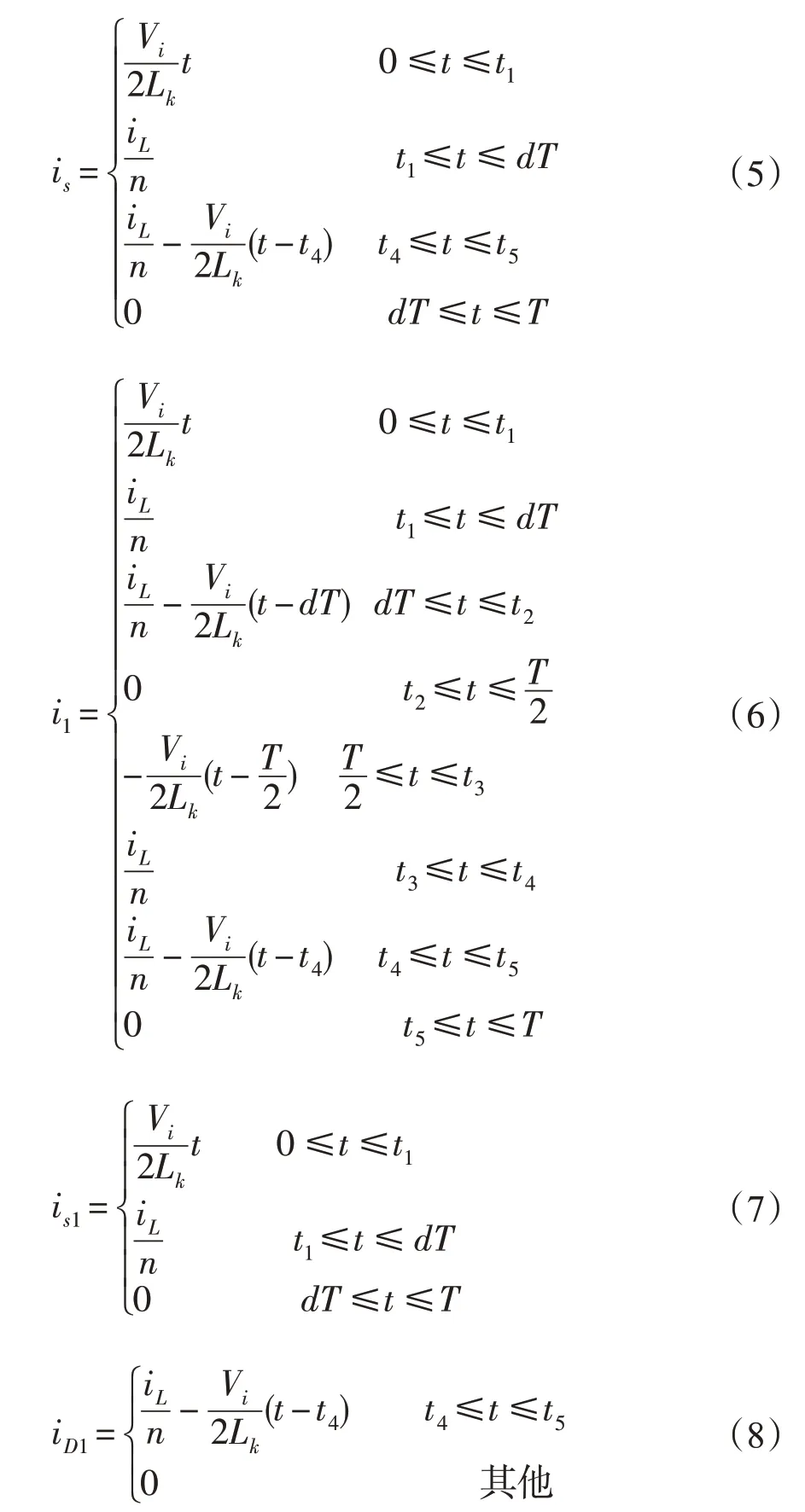
由以上各參量的瞬時值，可以分別得到相應參數的以下數值。

由式（12）和式（13）可以得到各元件寄生參數的功率：

由式（14）可以在平均化的電路模型中將開關管的開通電阻折算到輸出電感支路的等效值為

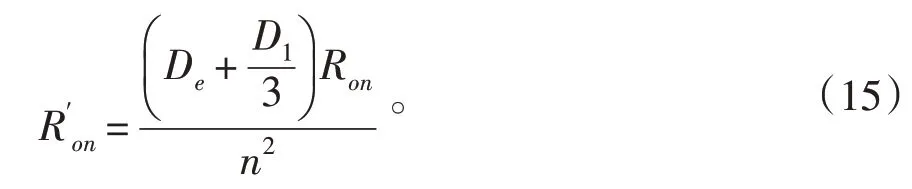
同理，其他寄生電阻也可以得到在平均化電路中的等效值。如下式：

通過整理式（15）和（16）可以得到折算后等效的總參數：

將原邊開關管和二極管用可控電流源替代，副邊二極管用可控電壓源替代之后，由式（12），（17），（18）可以得到圖2 經能量守恒平均電路法處理后的模型，如圖4所示。

圖4 等效模型

化簡得到如圖5所示電路。

圖5 化簡后的電路

2.2 半橋DCDC變換器傳遞函數

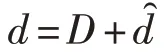
圖6 小信號模型

由圖6 可以得到輸出電壓對占空比的傳遞函數：

3 仿真計算

本文設計了一型半橋逆變全橋整流的DCDC 變換器。其主要參數為：輸入電壓Vi=700 V；開關頻率fs=18 kHz；功率開關管寄生電阻Ron=3.8×10-3Ω；快速回復二極管寄生電阻RF1，2=1.46×10-3Ω，開通壓降VF1，2=1.38 V；變壓器原變電阻RT1=1.15×10-3Ω，變壓器副邊電阻RT2=1.35×10-3Ω，變壓器漏感Lk=1×10-6H；整流二極管寄生電阻RF3～6=1.95×10-3Ω，整流二極管開通壓降VF3～6=1.43 V；輸出電感寄生電阻RL=1.3×10-3Ω，輸出電感L=1×10-3H；輸出電容寄生電阻RC=1×10-3Ω，輸出電容C=2.2×10-3F；負載電阻Ro=0.47 Ω；變壓器變比n=2.76；占空比D=0.45。

由以上各參數及式（17）可以得到：

因此，可以得到所設計的半橋逆變全橋整流DCDC 變換器輸出電壓對PWM 波占空比的傳遞函數：

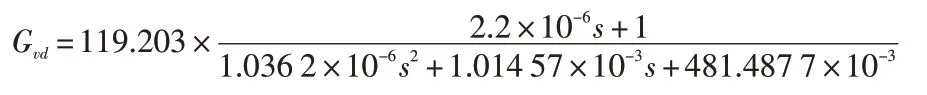
運用以上傳遞函數對所設計的變換器進行仿真。同時，在Simulink 環境下搭建系統電路進行仿真。兩種仿真方式的結果對比如圖7所示：

從仿真結果可以看出，基于能量守恒平均電路法所建立的半橋逆變全橋整流DCDC 變換器模型的仿真結果與在Simulink 環境下搭建同樣電路的仿真結果極為類似。證明了運用該方法建立變換器模型的可行性。

4 結語

本文運用能量守恒平均電路法詳細的討論了半橋逆變全橋整流DC-DC 變換器模型建立的過程，得到了變換后的等效模型和輸出電壓對控制PWM波占空比的傳遞函數。運用所得到的傳遞函數對所設計的一型半橋逆變全橋整流DCDC 變換器進行了分析。同時，在Simulink 環境下搭建了該變換器的電路。對比仿真結果，所建立的模型及其傳遞函數能夠正確的反映系統的運行特性，為指導設計提供依據。

圖7 仿真結果對比

［1］楊亞澤.基于等效小參量法的DC-DC開關變換器建模與仿真［D］.長沙：中南大學，2010.

［2］程心.非理想DC-DC 開關變換器的建模分析與仿真［D］.合肥：合肥工業大學，2009.

［3］宋受俊，劉景林，張智慧.BUCK變換器建模及其先進控制方法仿真［J］.計算機仿真，2006，23（3）：294-300.

［4］歐陽長蓮，嚴仰光.一種新的PWM DC-DC 變換器建模方法［J］.南京航空航天大學學報，2001，33（3）：254-258.