一類具p-Lap lace算子的邊值問題研究

王英博，丁 瑋

（上海師范大學數理學院，上海 200234）

一類具p-Lap lace算子的邊值問題研究

王英博，丁 瑋

（上海師范大學數理學院，上海 200234）

研究了一類具p-Laplace算子的二階三點邊值問題，并且給出這個邊值問題的格林函數.再利用上下解和單調迭代法，得出了這個方程極值解存在的充分條件.

p-Laplace算子；上下解；單調算子；線性邊值問題

0 引 言

邊值問題理論在微分方程中是非常重要的一個領域.在近些年，邊值問題由于其廣泛的理論與實際背景而備受關注，見文獻［1-7］.比如在物理學弦振動問題中，常常會遇到方程求解，這時就需要考慮實際背景，也就是要添加其邊值條件.研究邊值問題的方法有很多，文獻［ 1，2］利用Mawhin的延續定理，上下解問題［ 1，8］，單調迭代方法［3］，等等.在這些方法中，利用上下解和單調迭代方法是證明邊值問題極限解存在性的一種非常有用的方法，見［ 6， 7， 9，10］.

然而，由于有些問題的性質不同，使得對它們的研究更加困難.目前有很多文章［ 11，12］是研究線性邊值條件的，但研究非線性邊值條件的就比較少了［13］，而研究p-laplace算子的就更少了［ 14，15］.原因在于p-laplace算子會使問題變得更加復雜.

在這篇文章中，考慮了如下帶有p-laplace算子的邊值問題：

1 基本引理

引理1.1如果δ＞ 1，f∈C(I×R，R＋），下列邊值問題：

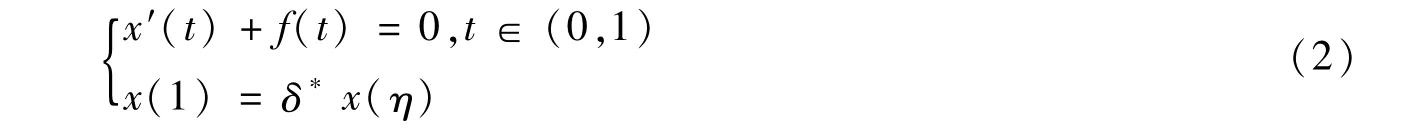
有唯一解，并且唯一解x(t）≤ 0，t∈( 0，1）.

證明 對(2）的第一個方程從η到t積分，得：

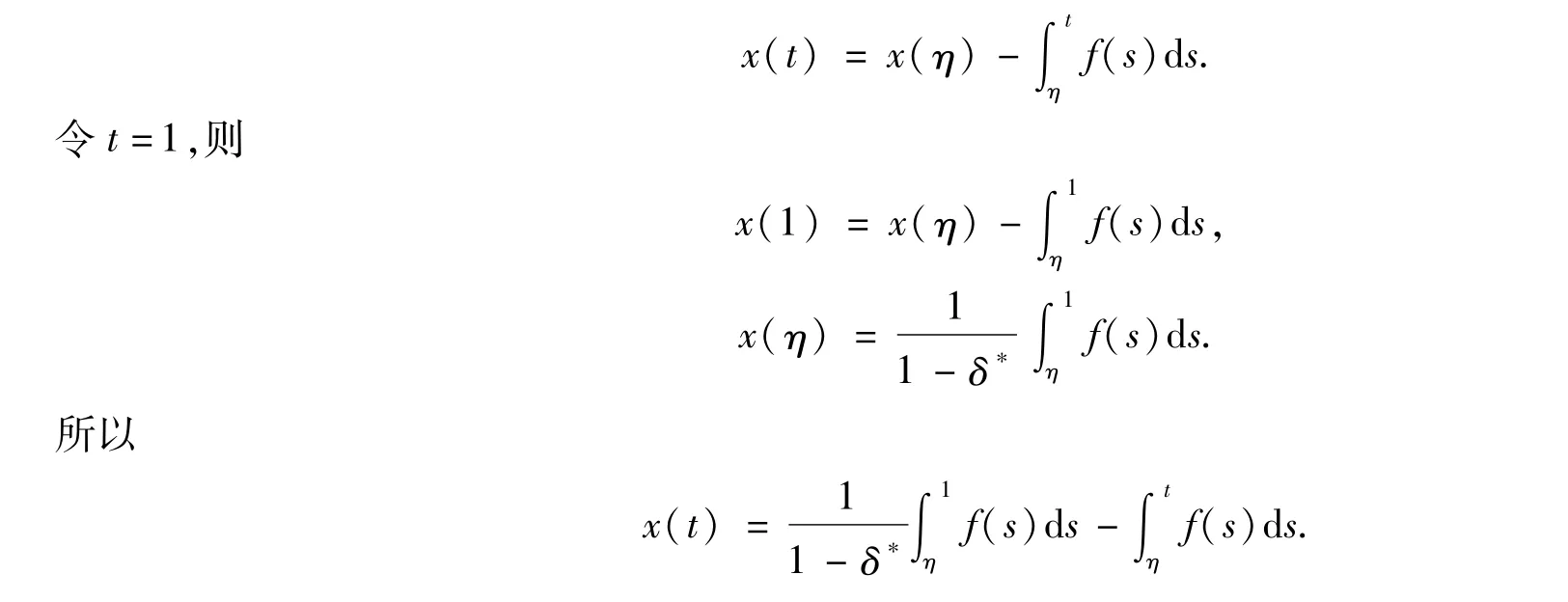
由δ＞ 1，f∈C(I×R，R＋）得x(t）≤ 0，利用引理1.1及其方法，可得下面的結論.

推論1.1如果δ＞ 1，f∈C(I，R＋），則邊值問題：

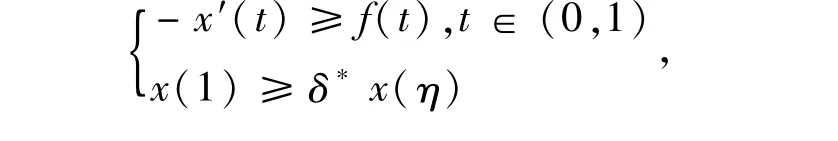
有解x(t）≤ 0，t∈( 0，1）.

引理1.2 如果δ＞ 1，則問題(1）有唯一解：

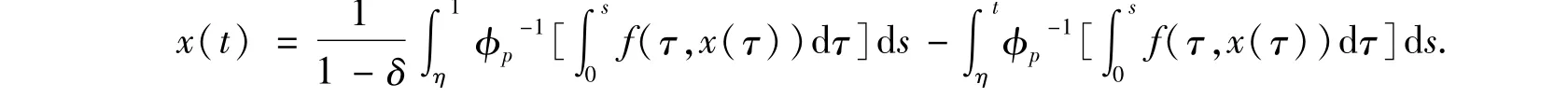
證明對(1）第一個方程從0到t積分，得

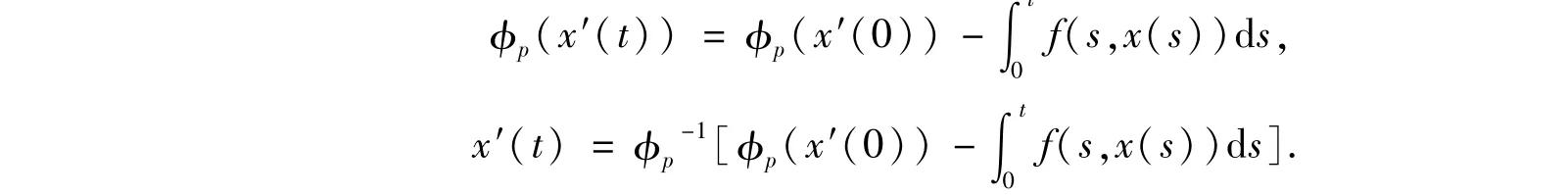
對上式從η到t積分，有：

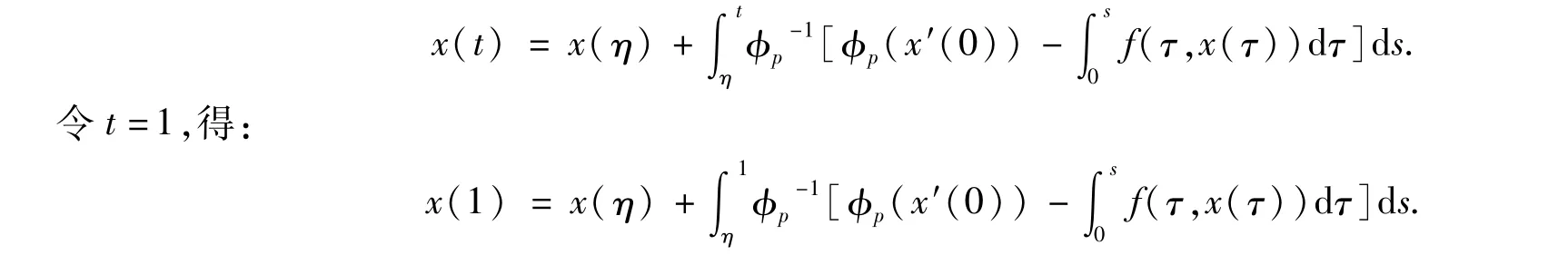
代入邊界條件x′(0）＝ 0，x(1）＝δx(η），得：

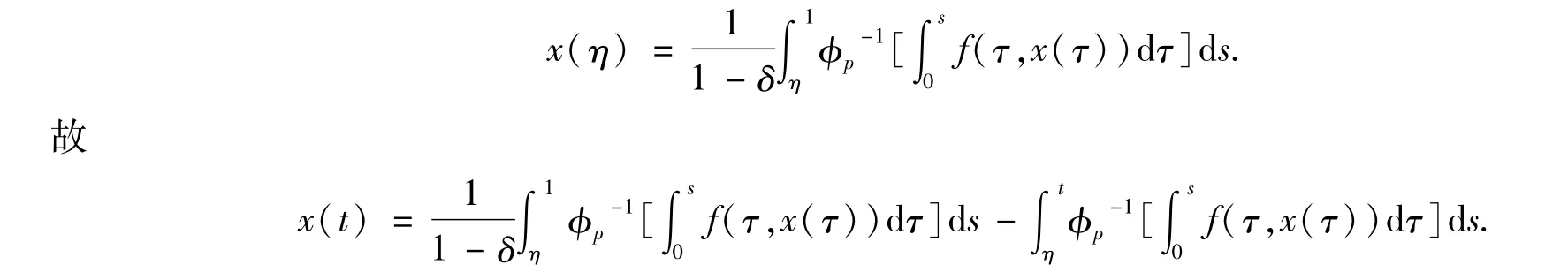
定義1.1α0被稱作邊值問題(1）的上解，當α0滿足下列條件：

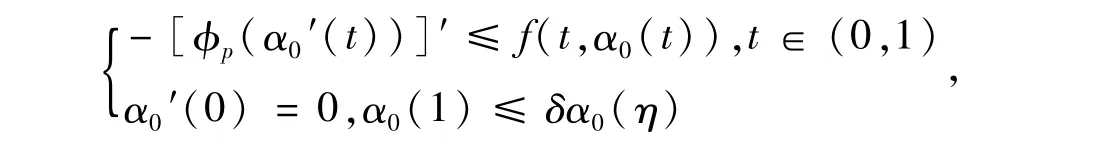
改變不等號的方向，可以定義邊值問題(1）的下解β0.

在本文中，定義空間C與算子A如下：

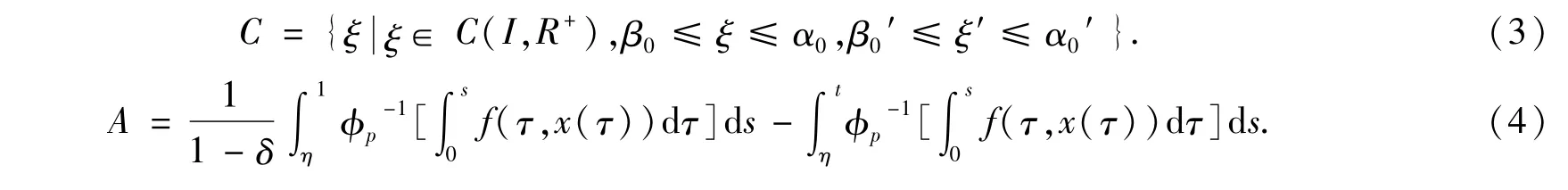
同時，下面兩個假設成立.

引理1.3假設(H1），(H2）成立，且δ＞ 1，則AC?C.

證明對?ξ∈C.令γ＝Aξ，由A的定義與引理1. 3，得：

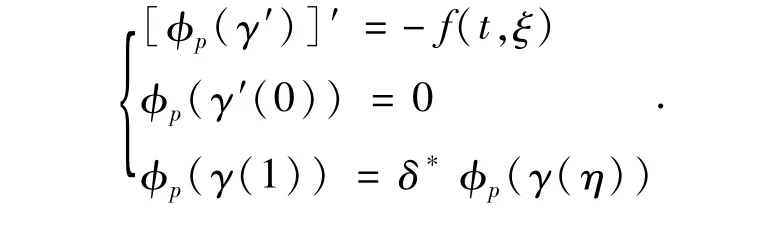
分兩步證明結論成立.

第一步，有：

根據推論1. 2，可得u≤ 0，則γ′≤α0′.

第二步，令v(t）＝γ(t）-α0(t），由第一步知v′(t）＝γ′(t）-α0′(t）≤ 0，由邊界條件v(1）＝δv(η），再根據引理1. 1，可得v≤ 0，則γ≤α0.

同理可證，γ≥β0，γ′≥β0′.

2 主要結果

對α0，β0∈C，定義β0≤α0，β0(t）≤α0(t），t∈( 0，1）.

定理2.1當(H1），(H2）成立，且δ＞ 1，設α0和β0是邊值問題(1）的下解和上解，并且有β0(t）≤α0(t），t∈( 0，1），則存在單調序列｛αn(t）｝(↘），｛βn(t）｝(↗）分別一致收斂與邊值問題(1）的極限解y*(t）與y*(t）.y*(t），y*(t）∈［β0，α0］.

證明將分4步證明.

第一步，證β0≤Aβ0，Aα0≤α0.由C的定義與引理1. 4，可以直接得出上述結論.

第二步，當β0≤ξ1≤ξ2≤α0時，證Aξ2≤Aξ1.

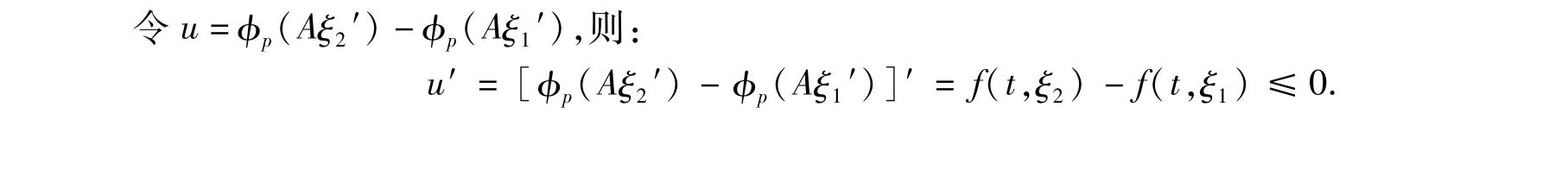
所以y*與y*是(1）的極限解.

［1］ GEW.Boundary value problems for nonlinear ordinary differential equations［M］.Beijing：Science Press，2007.

［2］ GEW，REN J.A extnsion of Mawhin′s continuation theorem and its application to boundary value problem with a p-laplacian［J］.Nonlinear Anal， 2004，58：447-448.

［3］ DINGW，HAN M.Periodic boundary value problems for second order impulsive functional differential equations［J］.Appli Math and Compu， 2004，155：709-726.

［4］ LAKSHMIKANTHAM V，BAINOV D D，SIMEONOV P S.Theory of impulsive differential equations［M］.Singapore：World Scientific，1989.

［5］ BAIZ，HUANG B，GEW.The iterative solutions for some fourth-order p-laplace equation boundary value problems［J］. Applied Math Lett， 2006，16：8-14.

［6］ NIETO J J，RODRIGUEZ-LOPEZ R.Remarks on periodic boundary value problems for fuctional differential equations［J］JCompu and Math with Appli， 2003，158：339-353.

［7］ NIETO J J，RODRIGUEZ-LOPEZR.Existence and approximation of solutions for nonlinear fuctional differential equations with periodic boundary value conditions［J］.JCompu and Math with Appli， 2000，40：433-442.

［8］ MA R.Multiple results for a three-point boundary value problem at resonance［J］.Nonlinear Anal， 2003，53：777-789.

［9］ DINGW，HANM.Periodic bundary value problems for second order functional differentialequations［J］.JMath Anal Appli， 2004，298：341-351.

［10］ LADDE G S，LAKSHMIKANTHAM V，VATSALA A S.Monotone Iterative Techniques for Nonlinear Differential Equations［M］.London：Pitman，1995.

［11］ LIF，SUN J.Monotone iterativemethod for the second-order three-point boundary value problem with upper and lower so-lutions in the reversed order［J］.Appli Math Compu， 2011，217：4840-4847.

［12］ WANGW，YANG X.Boundary value problems involving upper and lower solutions in reverse order［J］.JCompu and Math with Appli， 2009，230：1-7.

［13］ CABADA A，TOMECEK J.Nonlinear second-order equations with functional implicit impulses and nonlinear functional boundary conditions［J］.JMath Anal Appli，in Press.

［14］ ZHANG X，LIU L.Positive solutions of fourth-order four-pointboundary value problemswith p-Laplacian［J］.JMath Anal Appli， 2007，336：1414-1423.

［15］ SU H，WEIZ，，WANG B.The existence of positive solutions for a nonlinear four-point singular boundary value problem with a p-Laplacian operator［J］.Nonlinear Anal， 2007，66：2204-2217.

Nonlinear boundary value problem s w ith p-Laplace operator

WANG Yingbo，DINGWei
(College of Mathematics and Sciences，Shanghai Normal University，Shanghai 200234，China）

We study the second-order three-point boundary value problem with a p-Laplacian operator，and give the expressions of the Green's function for the boundary problems.By themonotone iterativemethod，sufficient conditions for extreme solutions are obtained.An example is given to illuminate the effectiveness of themain result.

p-Laplace operator；upper and lower solution；monotone operator；nonlinear boundary value problems

O 175.2

A

1000-5137(2013）02-0125-05

（責任編輯：馮珍珍）

2012-12-10

國家自然科學基金面上項目(11271261）

王英博(1986-），男，上海師范大學數理學院研究生；丁 瑋(1968-），女，上海師范大學數理學院教授.