基于人工蜂群改進算法的無線傳感器網絡定位算法

李牧東，熊 偉*，梁 青

(1．空軍工程大學信息與導航學院，西安710077;2．西安郵電學院電子與信息工程系，西安710121)

位置信息對傳感器網絡的監測活動至關重要，沒有位置信息的監測消息毫無意義[1]。如何確定無線傳感器網絡中節點的位置信息，成為了必須解決的關鍵問題。現有的無線傳感器網絡定位技術大體可分為基于測距和非測距兩類[2]。

DV-Hop算法是目前最受關注的無需測距的定位算法之一[3－4]。目前，已有很多關于經典 DV-Hop的改進算法，文獻[5]提出了通過先計算錨節點間的平均跳距得出誤差后再對網絡的平均跳距進行修正的方法;文獻[6]通過利用RSSI技術完成對未知節點與錨節點間距離的測量，從而提高了定位精度;文獻[7]對平均跳距進行加權處理并有選擇地選取錨節點進行定位從而減小定位誤差;文獻[8]將人工蜂群算法引入到DV-Hop算法未知節點計算階段從而提高了定位精度。

本文針對DV-Hop節點定位算法中采用多邊測量法計算未知節點坐標時產生較大誤差的問題，把節點定位問題轉化為最優化求解問題，結合人工蜂群算法(Artificial Bee Colony，ABC)的特點，在文獻[8]的基礎上，提出了自適應蜂群算法并將其應用于未知節點坐標的計算階段，以期減小定位誤差。

1 問題描述

DV-Hop算法是由Niculescu等人提出的，其定位過程分為3個步驟[3]:首先，使用典型的距離交換協議，使網絡中所有節點獲得距錨節點的最小跳數;其次，錨節點計算網絡平均跳距，并采用可控洪泛法廣播至整個網絡中，即每個節點僅記錄接收到的第1個平均跳距信息，而忽略之后接收到的;最后，通過未知節點通過所記錄的平均跳距和最小跳數信息計算自身到相應錨節點的距離，利用三邊測量原理或極大似然估計原理計算自身坐標。

在DV-Hop算法中，錨節點的平均跳距計算公式[4]如下

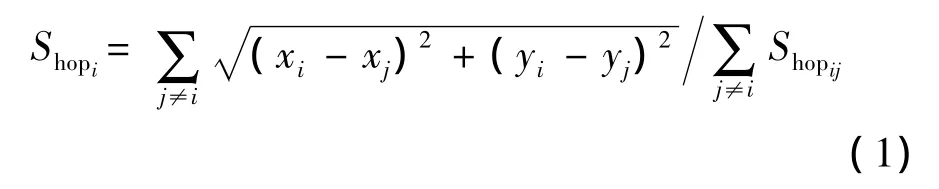
其中:Shopi是錨節點i對應的平均每跳距離，j為錨節點i數據表中的其他錨節點號，Shopij為錨節點i和j之間的跳數。

未知節點接收到平均跳距后，跟據所記錄的跳數信息，通過式(2)計算其到錨節點的距離:

通過上述計算后，傳統DV-Hop算法利用多邊測量法求解未知節點的坐標，從而完成定位，如圖1所示。

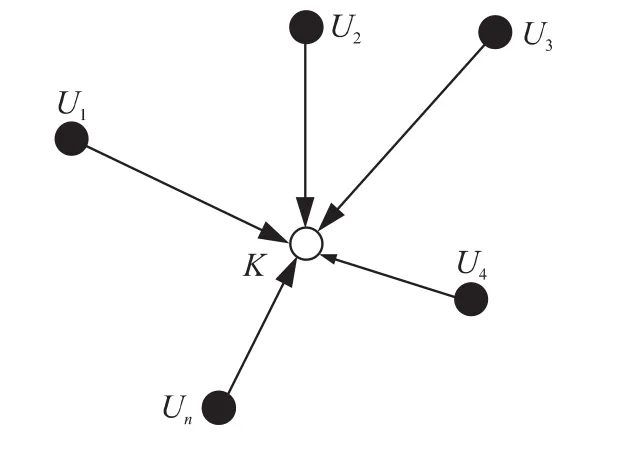
圖1 多邊測量法示意圖

若已知在n(n≥3)個錨節點時，U1(x1，y1)，U2(x2，y2)，…，Un(xn，yn)以及它們到未知節點 K(x，y)的測量距離分別為 d1，d2，…，dn，則有

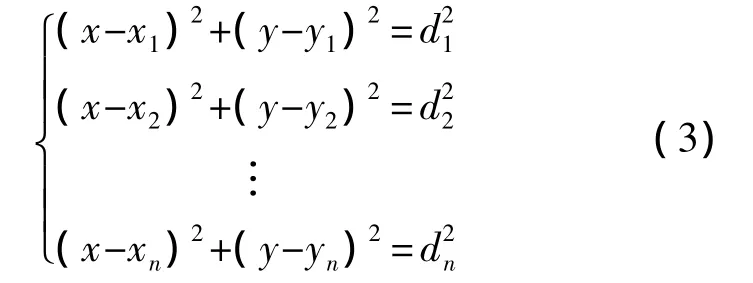
用方程組的前n－1個方程減去第n個方程后，得

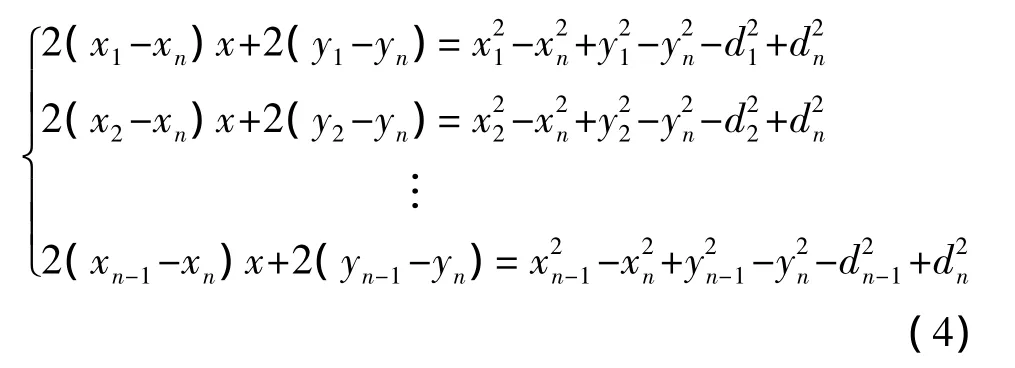
用線性方程組表示為AL=b，其中L=(x，y)T，

由于測距誤差、環境因素、通信等影響，測量距離總存在一定誤差，因此合理的線性方程組應該是AL+ε=b，ε為n－1維隨機誤差向量。使用標準的最小二乘法可以得到方程組的最小二乘解為L=(ATA)－1ATb。由于向量b中的每個元素都包含dn，而dn是帶有誤差的測量距離，因此所計算出結果的準確程度受制于dn。如果dn的誤差足夠小，那么求得的向量L還能滿足要求;若dn的誤差本來就很大，則求得的解的誤差也將很大。該方法雖然簡化了求解非線性方程組的過程，卻有可能犧牲解的精度，針對此情況，本文把問題轉化為全局最優化求解問題。

假設fn為未知節點到錨節點之間的測距誤差，則再由式(3)可知，對于未知節點坐標(x，y)滿足下式:

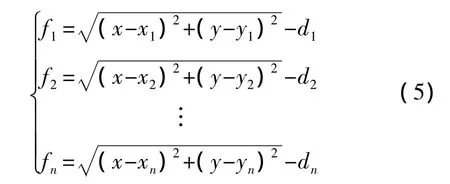
求解(x，y)，使得

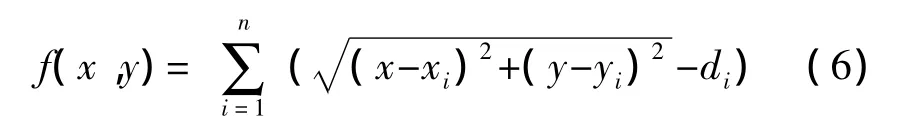
求解過程中，當由式(6)計算出來f(x，y)取最小值時，總誤差最小，則(x，y)的解最接近真實值，而此時的坐標(x，y)為最優解。由式(5)可知，f(x，y)的解不受限于某個方程，即當某個錨節點的測距誤差較大時，對于(x，y)的最終解影響也不大。

如上所述，便把節點定位問題轉化成全局最優化求解問題。對于式(6)的求解是個非線性最優化問題，如果用傳統的數學方法求解是很困難的。而人工蜂群算法是用來解決最優化問題中較為高效的方法，實驗結果表明，用人工蜂群算法求解最優化問題是行之有效的[9]。

2 改進人工蜂群算法求解最優化定位

2．1 ABC算法描述

人工蜂群算法ABC(Artificial Bee Colony)是由土耳其埃爾吉耶斯大學Karaboga在2005年提出的一種基于蜜蜂群智能搜索行為的優化算法[9]。在蜂群算法中，按照分工可將蜂群分為3類，即引領蜂、跟隨蜂和偵查蜂，其中引領蜂和跟隨蜂各占一半，并且引領蜂與蜜源的數量相等，用SN表示。首先，ABC算法初始化生成含有SN個蜜源(解)的初始蜂群;然后，引領蜂對所有的蜜源進行循環次數為C(C=1，2，…，N)的循環搜索，如果搜索到的蜜源的花蜜數量(適應度)優于以前的，則用新的蜜源位置代替舊的蜜源位置，否則保持舊的蜜源位置不變;最后，所有的引領蜂完成搜索之后，回到舞蹈區把蜜源上的信息分享給跟隨蜂，跟隨蜂則根據得到的信息依據貪婪機制選擇較優的蜜源。跟隨蜂選中蜜源后，也進行一次鄰域搜索，并保留較好的解。式(7)為引領蜂和跟隨蜂進行蜜源位置更新的公式:

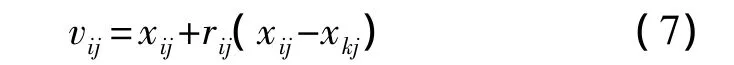
其中k為不同于i的蜜源，j為隨機選擇的下標，且k不等于 i，rij∈[－1，1]是一個隨機數，它控制 xij鄰域的生成范圍，隨著搜索接近最優解，鄰域的范圍會逐漸減小。ABC算法中跟隨蜂對蜜源的選擇是通過判斷蜜源的收益率大小來確定的，收益率通過適應度值來表示，選擇概率Pi按照式(8)確定，其中fiti是第i個解的適應度值，SN是解的個數。

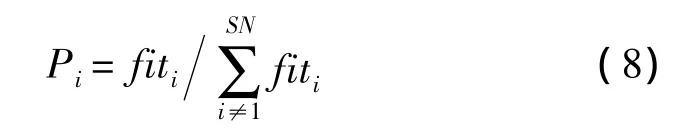
假定蜜源連續經過限定次數循環之后仍沒有得到改善，表明這個解陷入局部最優，那么這個位置就要被放棄，該位置的引領蜂轉變為偵查蜂。限定次數是ABC算法中重要的控制參數，用來控制對偵查蜂的選擇[10]。假設被放棄的解是xi，偵查蜂發現新位置并代替xi的操作如下。

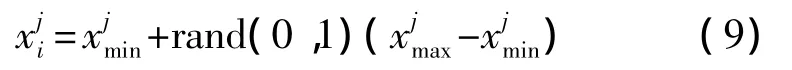
2．2 人工蜂群算法改進

人工蜂群算法中引領蜂對蜜源的搜索階段是影響整個算法全局及局部搜索能力的重要階段，在傳統人工蜂群算法中，由于rij的設置僅是在[－1，1]之間的隨機數，而沒有考慮引領蜂與跟隨蜂在位置更新時存在的聯系，具有較大的隨機性，從而導致在尋優求解過程中存在收斂速度慢、搜索精度低的缺點，嚴重影響了算法的性能。文獻[8]提出的基于人工蜂群算法的DV-Hop改進算法雖然在一定程度上提高了定位精度，但由于人工蜂群算法本身的局限性，算法的定位精度還有待進一步提高。本文在受到文獻[11]的啟發，對式(7)即引領蜂和跟隨蜂進行蜜源位置更新的公式，在文獻[8]的基礎上，引入自適應思想，提出了自適應人工蜂群算法AABC(Adaptive Artificial Bee Colony Algorithm)。

在引領蜂與跟隨蜂進行位置更新時，較大的rij有利于跳出局部極小值點，而較小的rij有利于算法的收斂[12]。對全局搜索通常較好的方法是在算法的初期使用較大的rij以通過較高的探索能力得到較優的蜜源，提高其搜索的精度，而在后期則需要較小的rij值，來提高算法的局部搜索能力以加快其收斂速度。因此將rij設計為迭代次數的函數，且隨著迭代次數逐漸遞減，并考慮到引領蜂與跟隨蜂的關系，將rij設置如下:

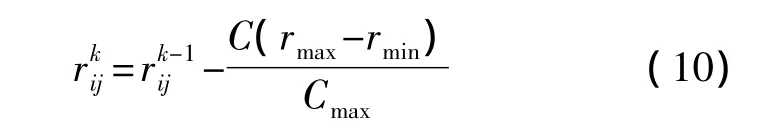
其中，rmin、rmax分別為初始和終止權重，Cmax為最大迭代次數，C為當前迭代次數。則引領蜂與跟隨蜂進行蜜源位置的更新公式改為:

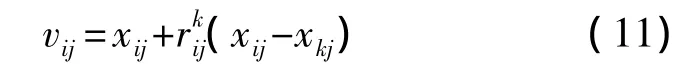
由此對蜜源位置的搜索趨勢起到了一定的引導作用，克服了算法本身隨機性強、收斂速度慢的缺陷。因此根據式(6)，定義本文適應度函數為:

其中，M為錨節點個數，則AABC算法主要步驟如下:

步驟1:設置主要初始參數:種群數、最大循環次數、參數維數、閾值等，其中引領蜂和跟隨蜂各占50%，偵查蜂1個;

步驟2:隨機產生SN個初始蜜源;

步驟3:引領蜂搜索蜜源，并根據式(12)計算蜜源適應度值，進入循環;

步驟4:跟隨蜂分享蜜源信息，由式(8)選擇其中一個蜜源，然后按式(11)搜索臨近新蜜源;

步驟5:對新蜜源計算適應度值，并根據貪婪機制選擇更優的蜜源;

步驟6:若循環至限定次數后，蜜源適應度值仍不達標則放棄，引領蜂變成偵查蜂繼續搜索，由式(9)更新位置;

步驟7:存儲此時的最優解;

步驟8:循環次數加1;

步驟9:滿足終止條件，達到最大循環次數。

2．3 結合AABC算法的DV-Hop改進

假設在一個無線傳感器網絡中總共存在N個節點，其中M個錨節點、N－M個未知節點，且錨節點坐標已知。根據DV-Hop算法原理，結合其定位過程，將AABC算法引入到 DV-Hop算法中，記為ADV-Hop，則基于AABC算法的DV-Hop算法定位流程如圖2所示。

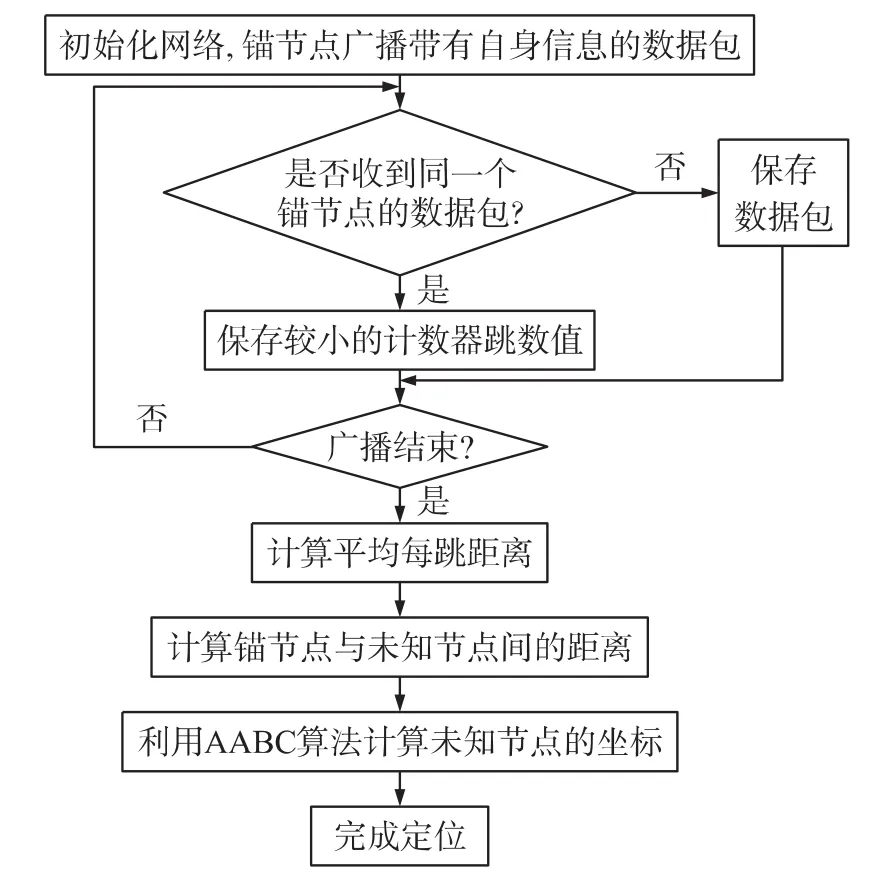
圖2 ADV-Hop算法的定位流程

3 性能分析

本文的實驗在Matlab平臺上進行，由于無線傳感器網絡節點受到體積、能量的限制，為了最大程度地減小本文改進算法ADV-Hop的定位誤差及能量消耗，設置循環次數C=30，引領蜂和跟隨蜂總數SN為50，且各占總數的一半，控制參數限定次數為10，rmin=0．4，rmax=1．2，r初始值設為 1，閾值 ε =10－6。假設所有錨節點坐標已知，節點隨機分布在邊長為100 m的方形區域內;未知節點和錨節點的坐標隨機產生;每個節點的通信半徑R=21 m。

假設各次仿真時的網絡區域、節點總數、錨節點總數、節點通信半徑等網絡參數相同，仿真次數為k=500，錨節點個數為m，節點個數為N，定位節點的真實坐標為，用統計的歸一化平均定位誤差、平均定位誤差均方差作為定位算法精度和穩定性的衡量指標。設ej、σj分別為仿真1次時的平均定位誤差和定位誤差均方差[13]。則基于k次仿真結果統計的歸一化平均定位誤差及歸一化的平均定位誤差的均方差分別為:

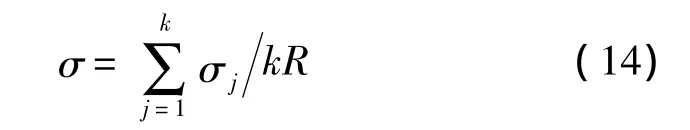
為了客觀地分析本文改進算法的定位性能，本實驗將文獻[8]提出的基于ABC算法的DV-Hop改進算法(記為BDV-Hop)，與利用最小二乘法計算未知節點的DV-Hop算法[4]一起，通過500次仿真實驗，與本文改進算法ADV-Hop進行比較。

圖3給出了100個節點隨機分布在方形區域內錨節點比例在5% ～40%變化時，歸一化平均定位誤差變化情況;圖4給出了相同條件下錨節點比例變化時，歸一化的定位誤差均方差的變化情況。從圖3、圖4可以看出:在節點總數和節點通信半徑不變的情況下，3種算法的平均定位誤差和均方差都隨著錨節點比例的增加而減小;另外，在相同條件下，ADV-Hop的平均定位誤差和均方差都明顯小于DV-Hop和BDV-Hop，具體的本文改進算法 ADVHop分別比DV-Hop歸一化的平均定位誤差平均減小了34．37%，較BDV-Hop平均減小了17．95%;而對應的歸一化的定位誤差均方差平均減小了21.58% 和 7．83%。

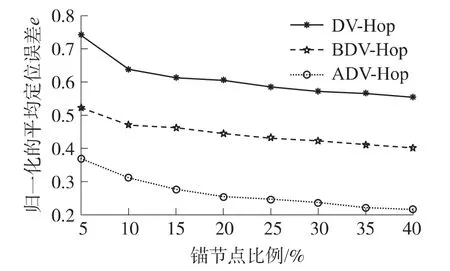
圖3 錨節點比例與歸一化的平均定位誤差關系

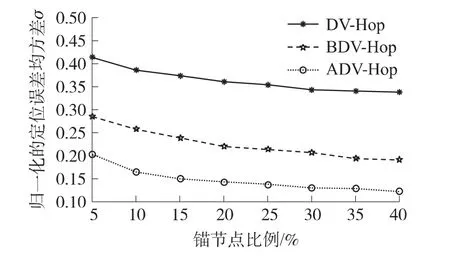
圖4 錨節點比例與歸一化的定位誤差均方差關系

圖5和圖6是在網絡區域內隨機選取10個錨節點，節點總數分別取 100、150、200、250、300、350、400時，各個算法的定位性能比較。從圖5、圖6可以看出，在錨節點不變的情況下，3種定位算法的定位誤差、定位誤差均方差都隨節點個數的增多而逐漸減小。ADV-Hop的定位誤差較DV-Hop平均減小了25．68%，較 BDV-Hop減小了10．15%，相應的誤差均方差分別平均減小了20．27%和7．38%。

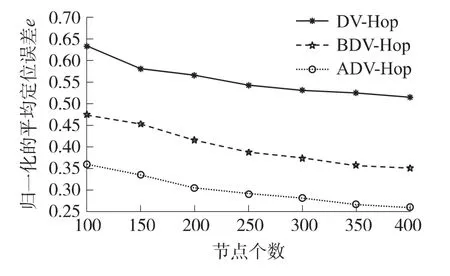
圖5 節點個數與歸一化的平均定位誤差關系

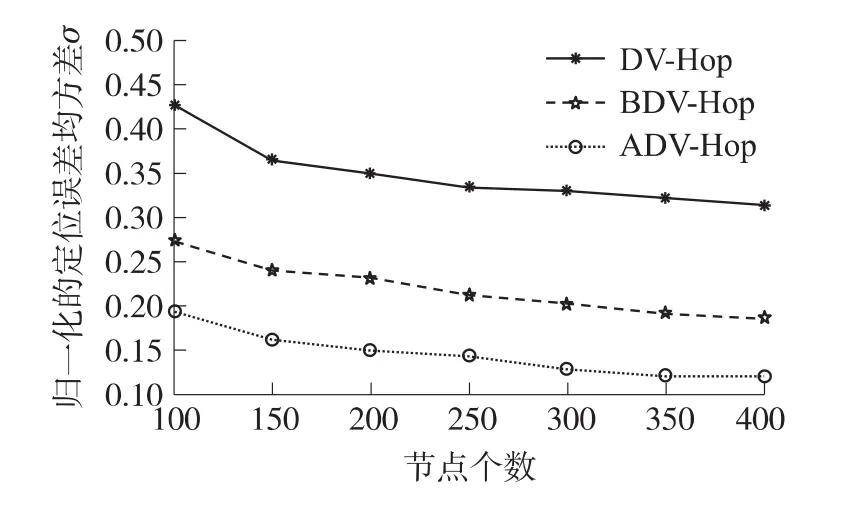
圖6 節點個數與歸一化的定位誤差均方差關系

從以上的結果分析中可以看出BDV-Hop算法在定位精度和穩定性方面都優于傳統DV-Hop算法，說明了將人工蜂群算法應用于無線傳感器網絡節點定位是一種可行的方案，另外相比于BDV-Hop算法，改進的ADV-Hop算法在定位精度和精度穩定性方面都有較大改善，有效地提高了算法的全局搜索能力以及收斂速度。

4 結束語

節點定位是無線傳感器網絡的應用基礎。本文在詳細分析DV-Hop算法中定位階段利用多邊測量法計算未知節點坐標過程的基礎上，成功將節點定位問題轉化為最優化求解問題，并利用ABC算法在解決最優化問題的優勢，結合定位具體問題，對ABC算法進行了改進，提出了基于改進ABC算法的ADV-Hop算法。該定位算法實現簡單，運行穩定，并且能夠有效地解決傳統DV-Hop算法采用多邊測量法估計未知節點坐標時定位誤差較大的問題，提高了算法在定位過程中的定位精度以及穩定性。仿真結果表明，ADV-Hop算法在不增加硬件開銷及略微增加計算開銷的基礎上，相比于傳統DV-Hop算法及BDV-Hop算法，在不同錨節點數和節點個數的條件下，明顯改善了算法的定位性能。

[1]Akyildiz I F，Weilian Su，Sankarasubramaniam Y，et al．A Survey on Sensor Networks[J]．IEEE Communications Magazine，2002，40(8):102－114．

[2]張震，閆連山，劉江濤，等．基于DV-Hop的無線傳感器網絡定位算法研究[J]．傳感技術學報，2011，24(10):1469－1472．

[3]姜鈞，程良倫．采用虛擬錨節點的高精度VAD-Hop定位算法[J]．傳感技術學報，2011，24(7):1048－1052．

[4]Niculescu D，Nath B．Ad-Hoc Positioning System(APS)[C]//Proceedings of the 2001 IEEE Global Telecommunications，2003，1734－1743．

[5]Dongxiao Liu，Yujun Kuang，Wei Wei．Research and Improvement of DVHOP Localization Algorithm in Wireless Sensor Networks[C]//Proceedings of International Conference on Computational Photography，2010，47－50．

[6]Fang Wangsheng，Yang Guangyu．Improvement Based on DV-Hop Localization Algorithm ofWirelessSensorNetwork[C]//Proceedings of International Conference on Mechatronic Science，Electric Engineering and Computer，2011，2421－2424．

[7]劉文遠，王恩爽，陳子軍．無線傳感器網絡中DV-Hop定位算法的改進[J]．小型微型計算機系統，2011，6(6):1071－1074．

[8]李牧東，熊偉，郭龍．基于人工蜂群算法的DV-Hop定位改進[J]．計算機科學，2013，40(1):33－36．

[9]Karaboga D．An Idea Based on Honey Bee Swarm for Numerical Optimization，Technical Report-TR06[R]．Kayseri:Erciyes University，Engineering Faculty，Computer Engineering Department，2005．

[10]Karaboga D，Basturk B．On the Performance of Artificial Bee Colony(ABC)Algorithm[J]．Applied Soft Computing，2008，8(1):687－697．

[11]陳貴敏，賈建援，韓騏．粒子群優化算法的慣性權值遞減策略研究[J]．西安交通大學學報，2006，40(1):53－56．

[12]Lei Xiujuan，Huang Xu，Zhang Aidong．Improved Artificial Bee Colony Algorithm and Its Application in Data Clustering[C]//Proc．of 2010 IEEE Fifth International Conference on Bio-Inspired Computing:Theories and Applications，2010，514－521．

[13]林金朝，陳曉冰，劉海波．基于平均跳距修正的無線傳感器網絡節點迭代定位算法[J]．通信學報，2009，30(10):107－113．