可識別聲源深度的三維聲聚焦波束形成方法*

丁 浩，李春曉，金江明，梅東挺，盧奐采，柴國鐘

(浙江工業大學機械工程學院，特種裝備制造與先進加工技術教育部/浙江省重點實驗室，杭州310014)

當前近場聲全息(Near-filedAcoustic Holography，NAH)[1]和波束形成[2]是對聲源在三維空間中進行識別定位的主要聲全息方法。NAH主要針對近場、中低頻的聲源識別定位，而波束形成方法有效地彌補了NAH在高頻和中、長距離的不足。目前波束形成方法結合傳聲器陣列信號處理技術已經廣泛應用于汽車、航空、雷達、通信、電子對抗和聲納等領域[4－6]。

如今人們對聲源的關注已經不僅僅局限于聲源究竟位于指定平面上的哪個位置，而更加關心復雜對象及復雜結構表面的聲場的三維空間分布狀況，而以往的研究主要著重于平面陣列結合波束形成方法識別定位聲源X、Y的坐標，但這類方法給出的聲場全息圖中不能揭示聲源的深度，所以無法識別定位聲源的三維坐標，其中包括相對于平面陣列的距離(深度)[2－3，7－12]，為解決這一問題，本文提出了可識別聲源深度的三維聲聚焦波束形成方法，該方法給出一系列聲場全息圖，通過跟蹤波束形成功率的最大點位置的軌跡確定聲源的深度，最終識別出聲源的三維坐標。

本文第1節給出了基于球面聲波傳播模型和波束形成方法，可識別聲源深度的三維聲聚焦波束形成方法的原理;第2節針對點聲源形成的聲場進行了仿真驗證，傳聲器布置依照B＆K60通道的輪輻陣列上傳聲器位置坐標[2];第3節在全消聲室內對仿真結果進行了實驗驗證;最后對研究結果進行了討論并給出本文的結論。

1 三維聲聚焦波束形成的原理和方法

通過由近及遠對垂直于z軸的不同距離的平面進行聲聚焦來完成對整個三維空間進行聲聚焦的原理，見圖1。移動間距定義為ΔZ，帶有網格虛擬平面稱為聚焦面，網格交點為聚焦點，同一個聚焦面上相鄰聚焦點沿x、y軸方向的間距ΔX和間距ΔY，聲聚焦即計算聚焦面上各個聚焦點上的歸一化后的波束形成聲功率相對輸出|B(r，ω)|2，稱為聲場響應。

圖1 可識別聲源深度的三維聲聚焦波束形成方法的基本原理

圖1為基于球面波假設的波束形成基本原理示意圖，對于任意傳聲器陣列形狀，當陣列中陣元與聲源的距離符合近場條件[7]時，聲源輻射的聲波假定為球面波，設定一點聲源坐標為(x0，y0，z0)，第m號傳聲器坐標為(xm，ym，zm)，m=1，2，…，M，其中 M為傳聲器個數。如設定1號傳聲器為參考傳聲器，其坐標為(x1，y1，z1)，那么參考傳聲器接收聲壓信號的表達式如式(1)所示[2]:

式中，P1(ω)為參考傳聲器接收到的聲壓信號;為聲源到參考傳聲器之間的距離;||表示向量取模;k=ω/c為波數;ω表示聲源角頻率;c是聲波的傳播速度;P0為聲源的強度。

第m號傳聲器相對于參考傳聲器的延時時間Δt'm(r)如式(2)所示:

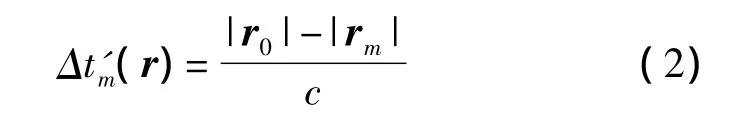
由于聲源輻射的聲波假定為球面波，傳聲器遠離聲源時，接收到的聲壓信號會有幅值衰減，所以第m號傳聲器相對于參考傳聲器接收聲壓信號的表達式如式(3)所示[2]:

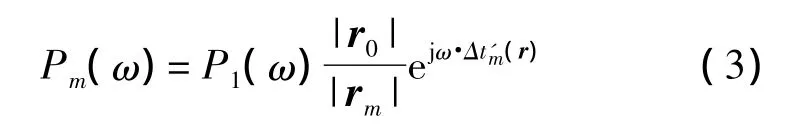
當將傳聲器測量到的聲壓逆向映射到第k個聚焦面上的聚焦點(xf，yf，zk)時，k=1，2，…，K，其中 K為聚焦面個數，設為參考傳聲器到聚焦點的距離，為第m號傳聲器到聚焦點的距離，Δrm(r)=|rc|－|rfm|，那么第m號傳聲器相對于參考傳聲器的延時時間Δtm(r)如式(4)所示:

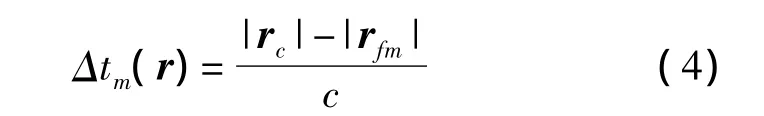
根據延遲求和原理，對各傳聲器信號進行相位延遲量Δtm(r)的補償后求和。按傳聲器通道數目M，再對聲壓進行歸一化的結果如式(5)所示[2]:

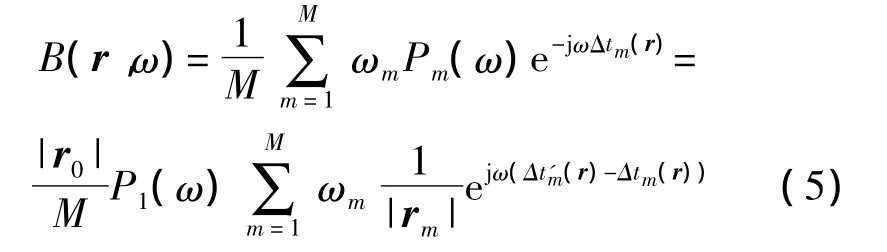
式中，ωm是第m號傳聲器的加權系數;B(r，ω)為波束形成歸一化聲壓復數相對輸出，相對于聚焦點的實際輸出。

對式(5)取功率后根據復數的三角不等式[13]得

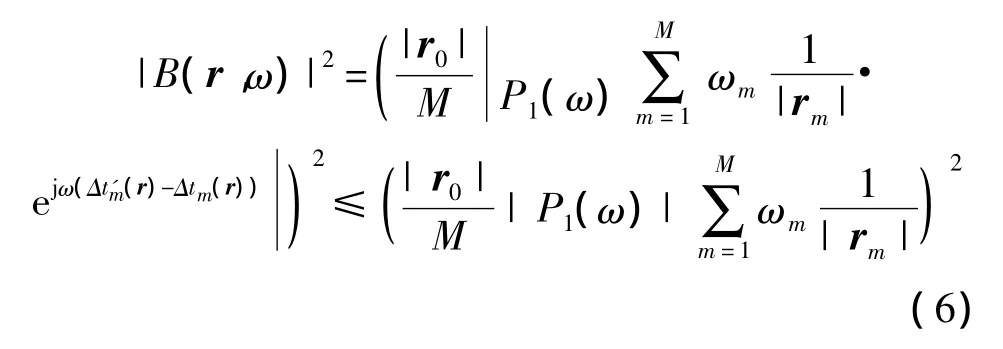
式中，|B(r，ω)|2為波束形成歸一化聲壓功率相對輸出。

由式(6)可知，當且僅當式(7)成立時，|B(r，ω)|2取得最大值，文中也稱為聲場響應的最大值。|B(r，ω)|2的最大值所在的空間位置也稱為聲場響應的最大值對應的空間位置。

根據各個聚焦面上聲場響應的最大值沿z軸方向的軌跡變化來搜索在該方向上具有最大聲場響應的聚焦面，從而判斷聲源在z軸方向的位置，再進一步根據該聚焦面上的聲場響應分布，搜索該面上的最大聲場響應點，來確定聲源在x軸和y軸方向的位置。

2 仿真及驗證

2．1 仿真流程和條件

本文用Matlab軟件仿真，設聲聚焦空間為長方體，其中心位于坐標原點，按照先驗值假定其邊界條件為－1 m≤xf≤1 m、－1 m≤yf≤1 m、0 m≤zk≤4 m，設 ΔX、ΔY均為0．01 m，ΔZ 為0．1 m，Z 方向采用步進掃描，即Zk+1=Zk+ΔZ。假設目標聲源為點聲源，考慮到測量誤差，假定傳聲器接收到的聲壓信號包含10%的測量噪聲，單聲源情況下，聲源x坐標x0為0.04 m，聲源y坐標y0為－0．08 m，聲源深度 z0分別為0．5 m、1．5 m、2．5 m 三種情況，聲源頻率為1 kHz、2．5 kHz、4 kHz;多聲源情況下，聲源1 的 x 坐標 xs1為－0．3 m，y 坐標ys1為－0．3 m，聲源深度zs1為0．5 m，聲源2 的 x坐標 xs2為－0．3 m，y坐標 ys2為－0．3 m，聲源深度zs2分別為1．5 m，聲源頻率為4 kHz，聲源強度都為50 Pa。二維陣列選用B＆K的60通道的輪輻陣列，陣列面位于x、y坐標平面內，陣列面的中心位于坐標原點。仿真驗證可識別聲源深度的三維聲聚焦波束形成方法的有效性，仿真流程如圖2所示。

2．2 仿真結果及分析

根據前面設置的仿真參數，當聲源位置為(0．04，－0．08，1．5)m 時，通過 Matlab 軟件仿真可以得到所有聚焦點處|B(r，ω)|2的值在三維空間的分布，但是為了更清楚的顯示識別定位結果，首先找到|B(r，ω)|2的最大值所在的空間位置，再選取與此空間位置共面同時又分別垂直于x、y、z軸的所有散點，最后經過篩選后的散點圖如圖3所示，同樣的方式可以得到多聲源的結果，如圖4所示。

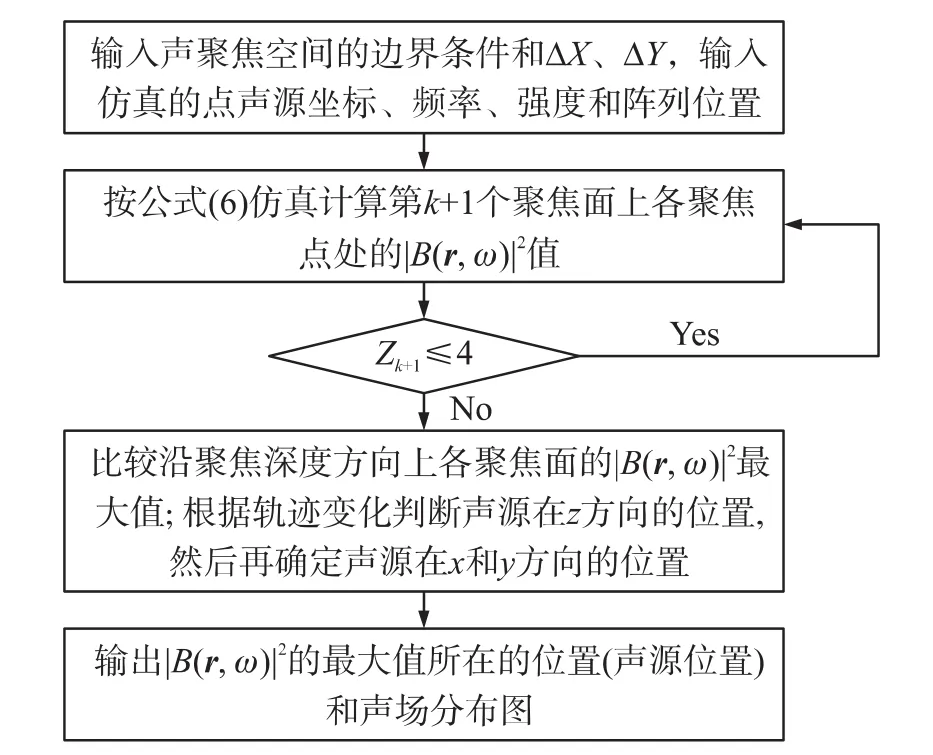
圖2 可識別聲源深度的三維聲聚焦波束形成方法識別定位聲源三維空間位置的仿真流程

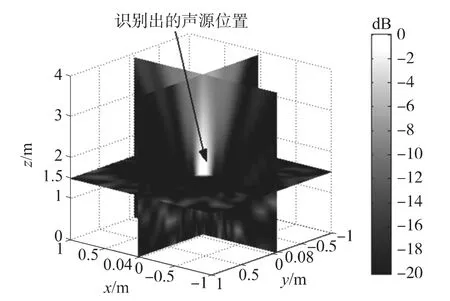
圖3 波束形成識別定位單個三維聲源仿真結果

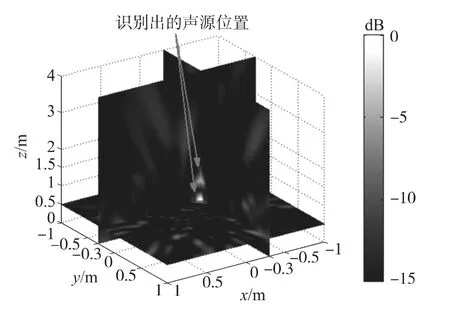
圖4 波束形成識別定位多個三維聲源仿真結果

由圖3、圖4可見，仿真結果表明通過輸出|B(r，ω)|2的最大值所在的空間位置可以同時識別定位單聲源或雙聲源的三維坐標。

為了進一步驗證聲源識別定位的有效性，分2步來顯示聲源識別定位的精度。

(1)側重于分析比較不同聲源深度條件下，該方法在z方向上的識別定位精度。

聚焦面在某一深度時，輸出此聚焦面上|B(r，ω)|2的最大值，隨著聚焦面平移，就得到|B(r，ω)|2的最大值隨zf的變化關系，最后分別模擬計算完3種聲源深度情況后，其結果如圖5所示。

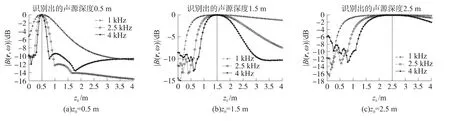
圖5 不同聲源深度條件下，聚焦面上|B(r，ω)|2的最大值隨zk的變化關系

(2)側重于分析比較聚焦面分別在不同聲源深度時，該方法在x、y方向上的識別定位精度。

當聲源頻率為4 kHz，聚焦面深度zk與聲源深度z0一致時，此聚焦面上的聲場分布情況如圖6所示。

圖6 不同聲源深度條件下，zk=z0時聚焦面上|B(r，ω)|2的全息圖

3 實驗驗證

3．1 實驗步驟和條件

實驗在浙江工業大學全消聲室內進行，消聲室的尺寸為3 m×3 m×3 m，本底噪聲為18 dB，最低截止頻率為63 Hz，利用輪輻陣列在全消聲室內測得的聲壓數據來驗證該方法的有效性和精度，實驗的陣列和聲源放置的相對位置關系如圖7所示。

圖7 實驗布置

小型揚聲器為目標聲源，選用B＆K的60通道輪輻陣列作為平面測量陣列，源和陣列的放置、聚焦的聲場各項參數及空間坐標系的設定與仿真時一致。實驗過程中，單聲源情況下，聲源x坐標x0為0．04 m，聲源y坐標y0為－0．08 m，為了在實驗驗證過程中，能夠通過計算聲源識別定位誤差來量化衡量聲源深度及頻率對本方法識別定位精度的影響，設置聲源深度z0范圍為0．25 m～2．5 m，深度變化間隔為0．25 m，聲源發出矩形脈沖信號，信號強度為30 dB，持續時間為10 s，頻率分別為500 Hz～4 kHz，頻率變化間隔為500 Hz，進行多次試驗測量;多聲源情況下，聲源1 的 x坐標 xs1為－0．3 m，y坐標 ys1為－0．3 m，聲源深度 zs1為0．5 m，聲源 2 的 x坐標 xs2為－0．3 m，y坐標 ys2為－0．3 m，聲源深度 zs2分別為 1．5 m，聲源頻率為4 kHz。輪輻陣列采用的是B＆K 4958傳聲器，有效工作頻率范圍10 Hz～20 000 Hz，動態范圍為28 d～140 dB，輪輻陣列的傳聲器布置為不規則布置，因此可有效避免柵瓣的產生。

3．2 實驗結果及分析

根據陣列測得的聲壓數據結合仿真時給出的參數，通過Matlab軟件得到|B(r，ω)|2的最大值所在的空間位置，散點圖如圖8所示，同樣的方式可以得到多聲源的結果，如圖9所示。

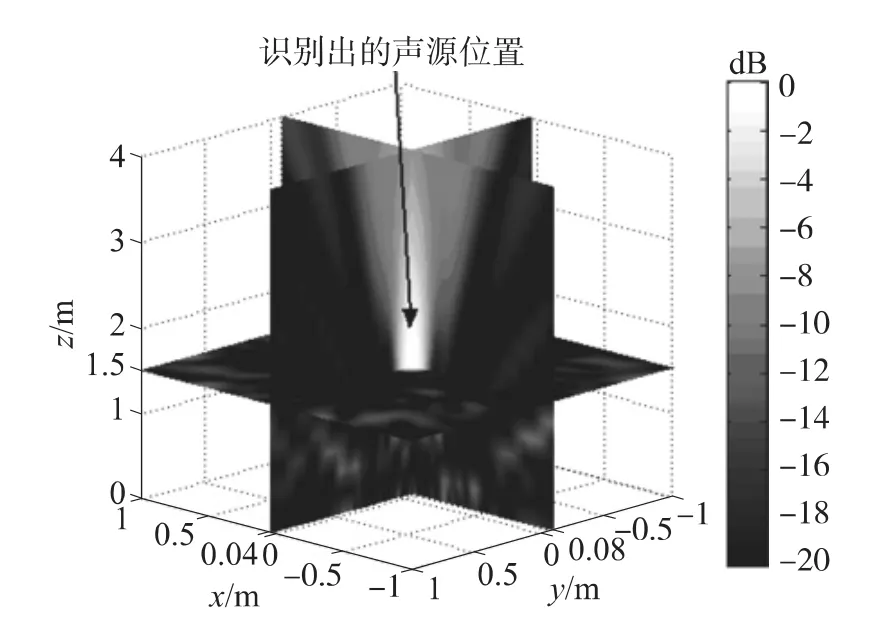
圖8 波束形成識別定位單個三維聲源實驗結果

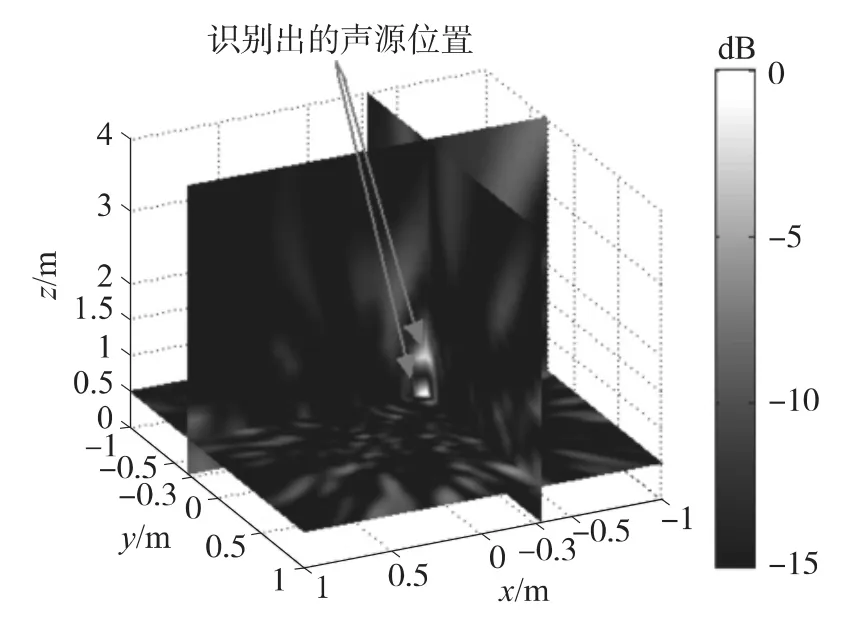
圖9 波束形成識別定位多個三維聲源實驗結果

圖10 不同聲源深度條件下，各聚焦面上|B(r，ω)|2的最大值隨zk的變化關系

由于聲源深度是變化的，考慮到單聲源實驗結果較多，將全部單聲源實驗結果給出較為累贅，而0．5 m、1．5 m、2．5 m 這3 個聲源深度的實驗結果能夠充分體現聲源深度對于定位精度的影響，并且便于和仿真結果比對，因此只給出這3個聲源深度條件下，聚焦面上|B(r，ω)|2的最大值隨zk的變化關系，和 zk=z0時，聚焦面上|B(r，ω)|2的值隨 xf、yf的變化關系，如圖8、圖9所示。

對比圖3與圖8，圖4與圖9，仿真和實驗結果吻合，表明通過輸出|B(r，ω)|2的最大值所在的空間位置可以同時識別定位單聲源和多聲源的三維坐標。

對比圖5和圖10，仿真和實驗結果一致表明所有聚焦面中|B(r，ω)|2的最大值相對應的zk與聲源深度一致，即可以準確識別定位聲源的z坐標;聲源頻率和聲源深度變化時，仍可以準確識別定位聲源的z坐標;聲源在z方向上的識別定位精度與聲源距平面陣列的距離有關，距離越遠，z方向空間分辨率越低，同時，聲源在z方向上的識別定位精度與三維空間在z軸方向上劃分的間距有關，間距越小，聲源識別定位的精度越高，同時也會增加計算時間。

對比圖6和圖11，結果表明聚焦面在聲源深度位置時，波束形成輸出的最大值所在的x、y平面坐標與聲源的x、y坐標一致，即該方法在智能確定深度的前提下，能同時準確的識別定位聲源的x、y坐標;然而隨著聲源深度的增大，該方法的空間分辨率會逐漸變差。

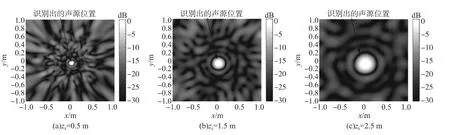
圖11 不同聲源深度條件下，zf=z0時聚焦面上|B(r，ω)|2的全息圖

為量化衡量本方法的識別定位精度，引入了聲源識別定位誤差的定義，聲源識別定位誤差δ為:

式中，ξ0為實際聲源X坐標或Y坐標或Z坐標，ξ為聲源X坐標或Y坐標或Z坐標的預測值。

如圖12所示，單聲源情況下在不同的深度條件時，X、Y、Z方向上的聲源識別定位誤差都保持在15%以內，特別是深度在2 m以內時，識別定位誤差都保持在10%以內，但隨著聲源深度的增大，識別定位誤差趨于上升，該方法的空間分辨率逐漸降低。

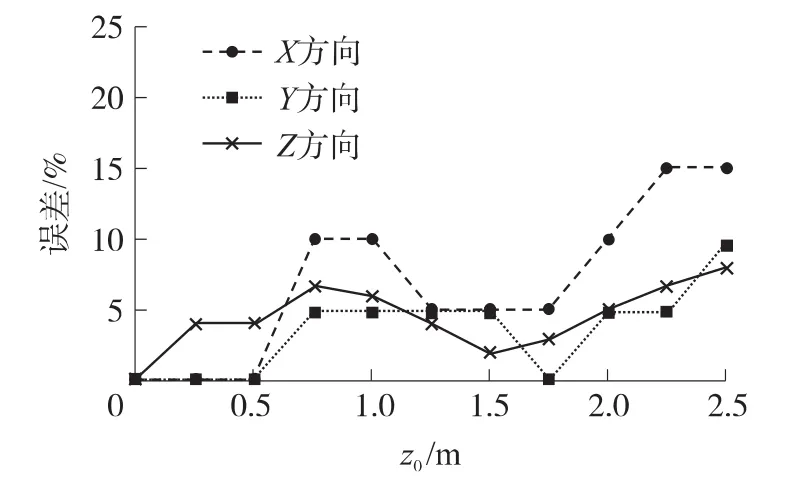
圖12 不同聲源深度條件下，聲源頻率4 000 Hz時，X、Y、Z方向上的聲源識別定位誤差曲線圖

如圖13所示，不同聲源頻率條件下，X、Y、Z方向上的聲源識別定位誤差都保持在20%內，特別是頻率在3 000 Hz以上時，識別定位誤差都保持在10%以內，隨著聲源頻率的增高，識別定位誤差趨于下降，該方法的空間分辨率逐漸提高。

圖13 不同聲源頻率條件下，聲源深度1．5 m時，X、Y、Z方向上的聲源識別定位誤差曲線圖

4 結論

基于球面波波束形成理論，提出了可識別聲源深度的三維聲聚焦波束形成方法，并借助點聲源模型模擬計算了聲源的聲場分布圖。仿真和實驗結果吻合，從而論證了該方法的有效性和精度。取得的主要結論如下:

(1)可識別聲源深度的三維聲聚焦波束形成方法能夠識別定位聲源的三維空間位置。

(2)隨著聲源深度的增大，識別定位誤差趨于上升，該方法的空間分辨率會逐漸降低，在2 m以內的范圍，有較好的空間分辨率。

(3)隨著聲源頻率的增高，識別定位誤差趨于下降，該方法的空間分辨率會逐漸提高，尤其在3 000 Hz以上的中、高頻，有較好的空間分辨率。

該方法還應在這幾方面進行完善:在單聲源識別定位時，空間分辨率隨聲源深度的增加而下滑較快，尋求提高空間分辨率的方法，以及解決有關聚焦面大小形狀和網格大小形狀等參數選擇的最優化、智能化等問題;進一步研究在多聲源識別時，該方法的識別能力;探討除測量噪聲外，陣元安裝誤差、混淆誤差等其他測量誤差[14－16]對聲源定位所帶來的影響。

[1]Parthy A，Van Schaik C J A A．Acoustic Holography with a Concentric Rigid and Open Spherical Microphone Array[J]．2009，1(5):2173－2176．

[2]Christensen J J，Hald J．Beamforming[J]．B＆K Technical Review，2004(1):1－31．

[3]張金圈，畢傳興，陳心昭．Beamforming方法的陣列研究及其在噪聲源識別中的應用[J]．噪聲與振動控制，2009，29(3):54－58．

[4]Kirkebo J E，Austeng A．Improved Beamforming Using Curved Sparse 2D Arrays in Ultrasound[J]．Ultrasonics，2007，46(2):119－128．

[5]Van Veen B D，Buckley K M．Beamforming:A Versatile Approach to Spatial Filtering[J]．ASSP Magazine，IEEE，1988，5(2):4－24．

[6]Bai M R，Lee J．Industrial Noise Source Identification by Using an Acoustic Beamforming System[J]．Journal of Vibration and Acoustics，1998，120(2):426－433．

[7]褚志剛，楊洋，蔣忠翰．波束形成傳聲器陣列性能研究[J]．傳感技術學報，2011，24(5):665－670．

[8]Kennedy R A，Abhayapala T D，Ward D B．Broadband Nearfield Beamforming Using a Radial Beampattern Transformation[J]．IEEE Transactions on Signal Processing，1998，46(8):2147－2156．

[9]Dhanantwari A C，Stergiopoulos S，Song L，et al．An Efficient 3D Beamformer Implementation for Real-Time 4D Ultrasound Systems Deploying Planar Array Probes[J]．IEEE Ultrasonics Symposium，2004，2:1421－1424

[10]Karl B Washburn，Tony Frazer，Jason Kunio．Correlating Noise Sources Identified by Beamforming with Sound Power Measurements[C]//SAE，2005－01－2510．

[11]Mukwevho Tshilidzi，Jordaan Jaco，Noel Guillaume．Advanced Beamforming Techniques for Acoustic Source Localization[C]//IEEE Africon Conference，2009，5308363．

[12]Arye Nehorai M，Kwok-Chiang Ho，B．T．G．Tan Minimum-Noise-Variance Beamformer with an Electromagnetic Vector Sensor[J]．Ieee transactions on signal processing，1999，47(3):601－618．

[13]Hardy G H，Littlewood J E，Pólya G．不等式[M]．2 版．北京:世界圖書出版社，2004:3．

[14]翟春平．劉雨東．聚焦波束形成聲圖法誤差分析[J]．聲學技術，2008，27(1):18－24．

[15]余毅，謝植廣，陳晟．球體表面圓環陣模態域波束形成誤差分析[J]．電聲技術，2010，34(10):69－72．

[16]賈瑞武，石庚辰．四元聲傳感器面陣快速測向算法及誤差分析[J]．傳感技術學報，2009，22(12):1757－1762．