航空發動機腔內積油引發振動故障分析

姜廣義，武 鵬，張 潔

（中航工業沈陽發動機設計研究所，沈陽 110015）

0 引言

航空發動機壓氣機結構大多采用鼓筒方式，其前后支撐的封嚴裝置在發動機調試和試制過程中漏油現象時有發生，導致鼓筒腔內積油。在轉子旋轉過程中，積油在一定條件下將發生自激振動，使轉子系統的振動異常。但由于流體的旋轉作用，使得這類問題的機理分析較一般的流固耦合問題更為復雜，而且還具有許多特殊性，成為目前轉子動力學研究領域的1個新課題[1-3]。

本文結合實際發動機試車過程中發生的異常振動，通過相關結構件模態分析、振動測試以及噪聲測試分析，最終找出振動異常原因。其經驗性結論可以在機理分析不完善情況下為振動故障診斷提供參考。

1 故障現象

某發動機在1次開車中剛進入慢車時發生喘振。此后，發動機在從起動到慢車過程中，以及慢車運轉一段時間后，會突發1種嗡鳴聲，同時振動總量突增。為此，將發動機下臺分解。分解時發現空氣導管軸心通風的甩油臺與低壓軸磨損，未見其它明顯故障，因此懷疑故障是氣動問題。將發動機重新裝配后上臺試車，原故障仍然存在。共開車2 3次后，再次將發動機下臺分解。發現如下故障點：（1）空氣導管軸心通風器甩油臺磨損；（2）低壓軸磨損；（3）高壓壓氣機工作葉片多級磨損，且輕重級分布為從后到前；（4）3支點外鋼套與軸承座磨損；（5）風扇第3級工作葉片磨損；（6）2支點石墨跑道磨損。將發動機再次裝配后上臺試車，該故障現象仍然存在。在第4次裝配中，在發動機軸承外環和3號軸承座間裝了銷釘，并將甩油孔件的甩油孔按原位改回，在其后試車過程中未再發生嗡鳴聲，一切正常。

2 原因分析

在發動機的聲音異常故障分析中，開始懷疑激振源是由氣動力引起的，因此在其后幾次試車中，對高壓壓氣機進氣和排氣都進行了監測，同時注意觀察各供油壓力，均未發現明顯變化以及與振動有關的現象，所以可以排除氣動因素影響。

2.1 結構分析

就該發動機結構而言，僅是調整了附件機匣的位置，并無其他變動，但該變化有可能會造成與之相關的結構件振動特性發生變化，從而誘發上述故障發生。為此，對幾次均發生磨損的空氣導管和中介機匣進行模態分析。

為較真實模擬空氣導管的實際安裝情況，在模態分析試驗中，將空氣導管和高壓渦輪盤等組合件支承于裝配架上，對應渦輪轉子在旋轉過程中的狀態，其結構的固有頻率見表1。

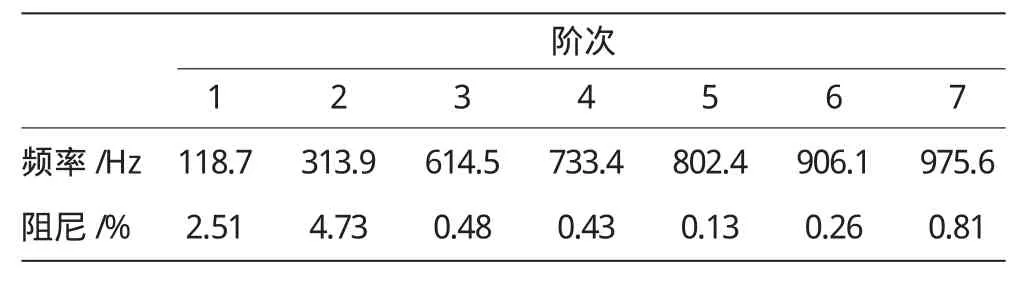
表1 空氣導管模態試驗結果

其中118.7Hz的固有頻率為1階彎曲形式，該頻率是1個不穩定值，隨盤所承受的載荷或渦輪轉子的氣動負荷變化而不同。如將該組合件用繩吊起做模態試驗，則其1階彎曲頻率為145Hz。但由于該類型空氣導管在多臺發動機中都有使用，以及在此臺發動機第1次上臺試車喘振前也未發生故障，所以可排除因其結構共振導致振動異常及出現嗡鳴聲。

中介機匣試驗件主要由支板、附件機匣、中央傳動齒輪和3支點軸承等組成，在附件機匣上同向等距離放置7個傳感器，測得的振型有1、2階彎曲振動，其固有頻率分別為20、110Hz。機匣振型由支板上放置的傳感器進行測試，其振型為1、2階彎曲振動，1階振型為158 Hz，而在機匣的直徑方向無振型存在。在發動機臺架試車時，附件機匣的確存在明顯的2階彎曲振型，1階振型頻率較低，約20～30Hz，2階振型頻率約為100～120Hz，1階振動固有頻率在慢車之前表現明顯，2階振型只有在軸承外環與軸承座松動時才有明顯表現。但從整機振動信號（如圖1所示）可見，發生振動異常和嗡鳴聲時，此異常頻率與轉速頻率并不重合，故判斷應不是因轉速頻率與此構件固有頻率耦合，從而誘發共振。

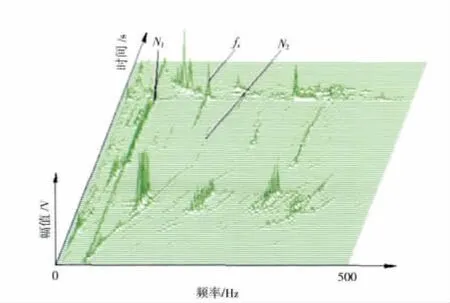
圖1 進氣機匣振動響應

2.2 轉子腔內積油自激振動分析

在發動機的幾次分解裝配過程中都發現高壓轉子內錐壁有積油現象，而積油的存在可能會引起轉子運動和轉子空腔內積液運動的相互作用。當轉子作無擾動的穩定自旋時，積油會均勻地貼于內壁，且與轉子一起以同一角速度自旋，無相對運動；但在一定條件下，積油產生自激現象，而不再與轉子一起同步擾動，積油的相對運動和壓力場對轉子產生1個附加力，與轉子的相互作用會使轉子以極大的振動作異步渦動，嚴重地影響轉子系統的正常運行，在一定轉速范圍內產生不穩定區。

整機振動測試的其它測點振動響應瀑布如圖2～4所示。

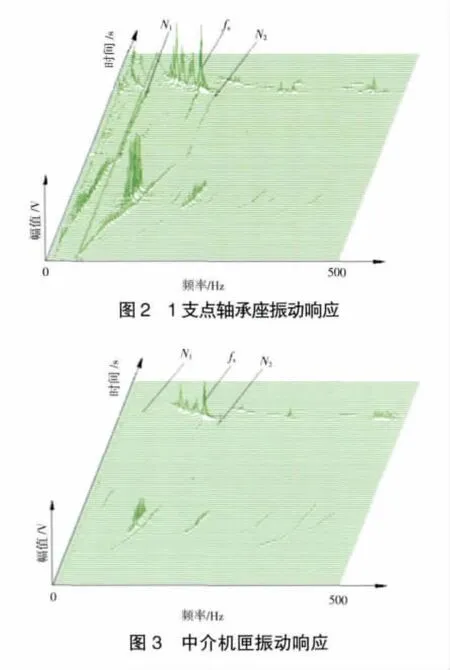
圖4 渦輪后機匣振動響應

從圖2～4中可見，fx頻率在一定轉速范圍內出現，并作異步渦動，幅值很大，所以fx頻率的出現應是因為腔內積油，并且在一定轉速范圍內出現自激現象的結果。

自從Kollmann[4]在試驗中觀察到部分充液轉子的不穩定現象后，已有一些學者開展了相關研究，但轉子系統基本上采用剛度各向同性的模型。Brommundt和Ostermeyer[5]及Holm和Trager[6]分別研究了支承剛度非對稱柔性懸臂轉子和剛性轉子系統的穩定性問題，發現由于支承剛度的非對稱使原來支承剛度對稱的部分充液轉子的1個不穩定區分裂為多個獨立的不穩定區，但并未說明出現多個獨立不穩定區的條件。祝長生[7]在2維無黏旋轉流體模型的基礎上，詳細地分析了支承剛度各向異性部分充液轉子系統的穩定性問題和轉子系統的各參數對穩定性的影響，認為影響系統穩定性的參數有充液量、質量比、外阻尼比、轉速比和支承剛度比；并認為支承剛度各向異性轉子系統的不穩定區可能是多個有限區間，分別與該系統的多個臨界區相對應。

從發動機起動到慢車停留過程中各振動測點頻譜圖中可見，共有2個不穩定區，對1支點軸承座所測振動響應數據進行整理，可得這2個不穩定區所對應的高壓轉子轉速范圍，如圖5所示。

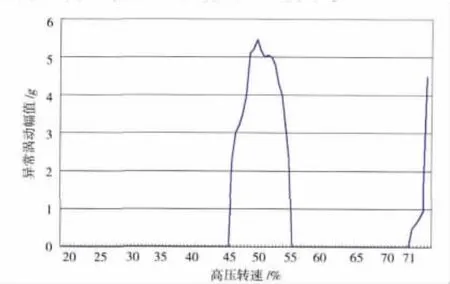
圖5 對應高壓轉速的不穩定區

從圖5中可見，高壓轉速從45%～55%最高轉速附近為第1個不穩定區，從71%最高轉速附近開始為第2個不穩定區。

使用MSC/PATRAN建立發動機轉子-支承系統分析模型，進行振動分析和后處理，得到高壓轉子激振臨界轉速計算結果。

通過與計算結果對比可知，在第1個不穩定區，異步渦動最大幅值的頻率為102.5Hz，對應于高壓轉子第3階臨界轉速，第2個不穩定區所對應的異步渦動最大幅值的頻率為147.5Hz，對應于高壓轉子的第4階臨界轉速。在發動機轉子腔內積油情況下，如果繼續增大轉速，由于多階臨界轉速的存在，積油也將存在于多個相對應的不穩定區。

文獻[8]研究了部分積液較多的兩端簡支的剛性轉子，并考慮了液壓梯度、流速等因素的影響，得到產生部分積液自激進動的失穩區為

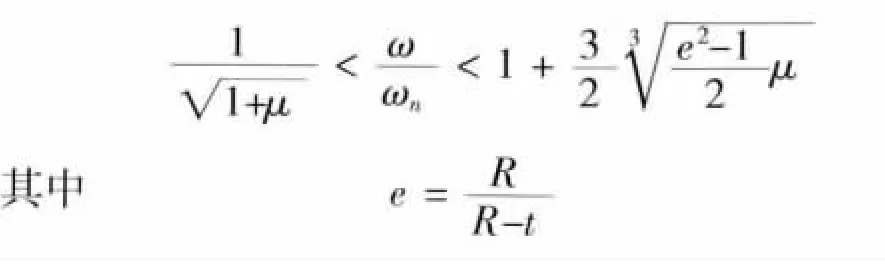
式中：R為空腔半徑；t為積液厚度；μ為黏度。

文獻[9]研究了兩端彈支轉子部分積液后的自激進動，得到的結果為失穩區有2個，相應在ω/ωn≈0.95～1.20及1.80～2.05。

針對該發動機，從整機振動1階高壓跟蹤幅值可知，該發動機的高壓轉子第3階臨界轉速為39.8%最高轉速，第4階臨界轉速為55.4%最高轉速。由于發動機在整個工作轉速范圍內無彎曲臨界，以上所述臨界振型都為剛體振型，所以發動機轉子可視為準剛性轉子，其第1個不穩定區的范圍為1.13＆lt;ω/ωn＆lt;1.36。

由于發動機轉速并未達到第2個不穩定區，所以無法確定其上邊界，其不穩定區范圍為1.29＆lt;ω/ω4＆lt;?。

2.3 振動異常時聲音分析

發動機在振動異常時會出現嗡鳴聲。在發動機第1次上臺1 6次開車中，為分析嗡鳴聲的頻率成分，增加了1個噪聲測試傳感器。在嗡鳴聲出現時，該傳感器所測噪聲信號的頻率成分如圖6所示。

從圖6中可見，出現嗡鳴聲時，噪聲的主要頻率成分fx與整機振動測點所測高壓轉子異步渦動頻率相吻合，即嗡鳴聲是因高壓轉子腔內的積油在自激情況下出現的。

圖6 聲振時噪聲測點所測頻率

2.4 磨損故障分析

在發動機分解過程中發現高壓壓氣機葉片、低壓軸等有多處磨損。從圖1～4中可見，當轉子腔內積油發生自激振動時，頻率成分明顯比振動正常情況時的豐富，并且包含轉子的倍頻成分，所以判斷在積油發生自激振動的同時，由于振動較大，導致發動機轉靜件發生多處碰摩[10]。

3 排故措施及驗證

在發動機轉子的鼓筒段和軸的內腔，如果存在設計不當，可能出現積油現象，將會改變整個轉子系統的振動特性。所以應在空腔的轉子上開甩油孔，使轉子在運轉過程中將油甩出，從而保證腔內無積油。

在該發動機第4次裝配中，將甩油孔件的甩油孔按原位改回，在其后試車過程中一切正常，未出現振動異常現象及嗡鳴聲。

通過以上分析，該發動機出現振動異常及嗡鳴聲的原因可以排除氣動因素以及結構件共振等因素，而是因高壓轉子內腔的積油，在特定轉速范圍內發生自激振動，該自激振動屬異步渦動，幅值較大，從而導致振動總量突增，使發動機轉靜件發生多處碰摩。由于發動機多個臨界轉速的存在，會出現多個相對應的不穩定區，而且不穩定區的下限轉速要大于臨界轉速。

4 結束語

針對腔內積油現象，目前主要以理論探索為主，所建試驗器也多為立式轉子試驗器。由于忽略了重力等因素影響，其試驗結論可能與臥式轉子有一定差異。如果能夠建立臥式轉子試驗器，以理論結合試驗進行研究，明晰故障特征和邊界條件，可在發動機設計和研制中更好地處理此類故障。

[1]張文. 轉子動力學理論基礎[M]. 北京：科學出版社，1990： 250-262.

ZHANG Wen. Theoretical basis on rotor dynamics[M]. Beijing： Science Press, 1990：250-262. (in Chinese)

聞邦椿，顧家柳，夏松波，等. 高等轉子動力學[M]. 北京：機械工業出版社，2000：194-198.

WEN Bangchun, GU Jialiu, XIA Songbo, et al. Advanced rotor dynamics [M]. Beijing：China Machine Press, 2000:194 -198. (in Chinese)

[3] 鐘一諤，何衍宗，王正. 轉子動力學[M]. 北京：清華大學出版社，1987：21-175.

ZHONG Yie, HE Yanzong, WANG Zheng. Rotor dynamics[M]. Beijing: Tsinghua University Press, 1987：21-175. (in Chinese)

[4] Kollmann F G. Experimentelle and theoretische unter-suchungen uber die kritischen drehzahlen flussigkeits-gefulter hohlkorper [J]. Forschund auf dem Gebiete des In-genieurw easns， 1962，28（B）：115-123,147-153.

[5] Brommundt E，Ostermeyer G P. Stability of a rotor partially filled with liquid and attached to an anisotropically mounted shaft[J]. Ingenieur-Archiv，1986，56（3）：379-388.

[6] Holm-Christensen O，Trager K. A note of instability caused by liquid motions[J]. Journal of Applied Mechanics, Transaction of ASME，1991，58（4）：801-811.

[7] 祝長生. 支承剛度各向異性部分充液轉子系統的穩定性[J].航空動力學報，2000，15（4）：432-434.

ZHU Changsheng. Stability of a rotor system on support of anisotropical rigidity and partially filled with an inviscid fluid [J]. Journal of Aerospace Power, 2000，15 （4）：432-434. (in Chinese)

[8] Colding-Jorgensen J. Rotor whirl measurements on a long rotating cylinder partially filled with liquid [J]. ASME DE, 1991,35: 127-131.

[9] Hendricks S L. Stability of a clamped-free rotor partially with liquid[J]. Journal of Applied Mechanics, Transaction of ASME，1986,53（1）: 166-172.

[10] 姜廣義，王娟，姜睿. 航空發動機風扇機匣振動故障分析[J]. 航空發動機，2011，37（5）：38-40.

JIANG Guangyi, WANG Juan, JIANG Rui. Vibration analysis of a fan casing in an aero-engine [J]. Aeroengine, 2011，37 （5）：38-40. (in Chinese)