一種基于SVD與EMD的多頻小信號檢測方法*

鄭 堂 李世平 羅 鵬 鄔肖敏

(第二炮兵工程大學，西安 710025)

0 引言

在工程實際中，測試得到的信號往往含有大量的噪聲，這嚴重影響了下一步對信號的處理和分析，同時，對于一個含有多個頻率成分的信號，需要知道其中所包含的具體頻率成分，就要對該信號進行分解。

在去除噪聲方面，奇異值分解(SVD)方法已經得到了成功應用并被證明是有效的[1-2]，SVD方法通過將反映噪聲的奇異值置零能夠有效的達到去除噪聲的目的。經驗模態分解(EMD)方法根據不同的時間尺度將信號分解為多個滿足一定條件的單一震蕩模式的線性疊加，每一個震蕩模式稱為一個本征模態函數(IMF)，通過這一方法，可以將信號中所包含的有用成分提取出來。

本文提出一種基于SVD與EMD相結合的方法，對于采集的信號，首先用SVD方法濾除噪聲，使信號的信噪比滿足EMD分解的要求，然后用EMD對信號進行分解，得到其中所包含的各頻率成分，最終達到檢測多頻小信號的目的。

1 SVD濾除噪聲原理

1.1 SVD相關理論[3]

設有m×n階矩陣：

(1)

假定其中n≤m，那么A的秩r≤n。存在n階正交陣V和m階正交陣U，使得：

UTAV=Λ

(2)

其中，Λ為m×n階非負對角陣，即：

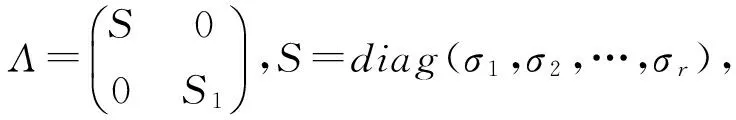
(3)

式中，σ1,σ2,…,σr和σr+1=σr+2=…=σn=0稱為A的奇異值；U、V的列向量分別為A的左右奇異向量。

對式(2)作等效變換可得：

A=UΛVT

(4)

上式就是矩陣的奇異值分解形式。

1.2 SVD去噪原理[4-6]

設含有噪聲的信號為：

f(n)=s(n)+u(n)

(5)

其中，s(n)為信號成分；u(n)為噪聲成分。設f(n)的信號長度為N，那么由f(n)可構造Hankel矩陣：

(6)

對F作SVD，它的奇異值σ1,σ2,…,σr可反映信號和噪聲能力集中的情況，將其按遞減順序排列，即σ(1)≥σ(2)≥…≥σ(r)，那么前i個較大的奇異值主要反映信號，后面較小的奇異值主要反映噪聲，將反映噪聲的奇異值置零即可達到去噪的目的。……