平板在任意周期表面熱擾動作用下的非Fourier熱傳導的求解與分析*

趙偉濤 吳九匯?

1)(西安交通大學機械學院，西安 710049)

2)(西安交通大學，機械結構強度與振動國家重點實驗室，西安 710049)

(2013年4月2日收到;2013年5月4日收到修改稿)

1 引言

自從17世紀Fourier建立了導熱的數學模型，Fourier定律隨之被廣泛應用于導熱問題分析的各個領域.對于熱作用時間較長的穩(wěn)態(tài)傳熱過程以及熱傳播速度較快的非穩(wěn)態(tài)常規(guī)傳熱過程，采用Fourier定律來描述熱流密度與溫度梯度之間的關系是可以滿足精度要求的.但是，Fourier定律不涉及傳熱時間項，隱含了熱擾動傳播速度為無限大的假設.隨著科學技術的進步，超短激光脈沖的出現和制冷水平的提高，存在著極高(低)溫條件下的傳熱問題和超急速傳熱問題，使得Fourier定律中的準平衡條件假設不再成立[1-4].

為了克服Fourier定律的局限性，Cattaneo[5]和Vernotte[6]分別獨立地提出了具有熱流延遲相的非Fourier熱傳導模型，計及熱流變化率對熱傳導的影響，其修正后的熱傳導方程為

其中，q是熱流矢量，T為溫度，k為熱傳導率，t是時間，τ0為熱松弛時間.方程(1)結合能量守恒方程得到以溫度T描述的雙曲線型熱傳導方程：

其中，a=k/(ρc)為熱擴散系數，ρ為密度，c為常應變比熱.

為描述熱以有限速度傳播這一超常規(guī)熱傳導現象，研究者們對方程(2)在不同初始條件和邊界條件下進行了求解.Tao等[7]采用數值模擬研究了固體激光器的非Fourier導熱問題.李世榮等[8]采用單相延遲模型，研究了薄板在受周期熱流邊界條件下板內的溫度響應.Sarkar和Haji-Sheikh[9]采用Laplace變換技術研究了由介電材料制成的有限平板的雙曲型熱傳導問題.Tang和Araki[10]求解了表面周期性加熱條件下有限介質的非Fourier熱傳導問題.Moosaie[11]在Tang等的工作基礎上，運用Fourier積分表達式，求解了有限介質在周期表面熱擾動條件下的非Fourier熱傳導問題.Barletta和Zanchini[12]分析了無限圓柱體存在內熱源以及與外界流體有熱對流的情況下的雙曲型熱傳導問題.Ate fi和Talaee[13]使用分離變量法求解了邊界條件不隨時間變化的無限長圓筒的非Fourier溫度場.Mishra和Sahai[14]運用格子Boltzmann法研究了一維圓柱和球體的非Fourier熱傳導問題.Jiang[15]運用Laplace變換法研究了空心球體在內外兩個表面溫度突然變化時的雙曲型熱傳導問題.Shirmohammadi和Moosaie[16]采用分離變量法得到空心球體在周期表面熱流條件下的解析解.

本文主要運用Duhamel積分和Fourier級數展開法得到平板前表面熱流任意周期變化時雙曲型熱傳導方程的解析解.首先采用Duhamel積分和分離變量法分析了方程在平板前表面遭受突變熱流和簡諧熱流這兩類特殊情況下解的形式，在此基礎上應用Fourier級數展開法和疊加原理研究了平板前表面熱流任意周期變化時解的形式.按照這些表達式，不同周期邊界條件下平板的雙曲線熱傳導行為得到分析和研究.這為工程應用和數值計算的驗證提供了便利.

2 數學模型

考慮一厚度為L，邊界絕緣，熱物性為常數的平板，假設其初始溫度T(x,0)=T0，從時間t=0時起，平板一表面x=0處(稱該表面為平板前表面，另一面稱平板后表面)遭受一熱流為q0·q(t)的作用.在這種情況下，由方程(2)可得一維平板的非Fourier熱傳導方程：

為了獲得方程(3)—(5)的無量綱形式，特引入以下無量綱量：

式中，Fo是 Fourier數，Ve是Vernotte數，1/Ve代表溫度波傳播的無量綱速度.

則方程(3)—(5)無量綱化之后為

3 分析求解

由于邊界條件(8)式中的f(Fo)是任意函數，這就使得直接求解方程(7)變得不可能.因此，首先假定f(Fo)為一時間無關量f，求解此條件下的溫度場;其次運用Duhamel積分，求解在任意函數f(Fo)下的溫度場.

設在邊界條件f下方程(7)的解為

當Ve→0時，方程(7)對應經典Fourier導熱的情形.此時βn為實數，(35)式變?yōu)?/p>

把(37)式代入(34)式可得經典Fourier導熱時平板內部的溫度場.

4 結果分析與討論

為了得到任意周期邊界條件下平板溫度場的解析解，將做如下遞進式推導.4.1給出了邊界條件為常數的情況;4.2的邊界條件為簡諧周期函數;4.3在前兩步的基礎上，計算與討論了邊界條件可用Fourier級數展開的任意周期函數的情況.

4.1 突變邊界條件

當厚度為L的平板前表面遭受大小為q0的突變熱擾動(q(t)=1)時，無量綱化后

此時(30)式就是方程(7)在邊界條件為常數下的解

對于Fourier導熱，當Ve→0時，方程的解為

根據(39)式，可以計算得到厚度為L的平板前面遭受一突變熱擾動時的溫度分布.為了驗證結果的可靠性，直接對方程(7)—(9)進行數值求解.圖1給出了平板前表面遭受突變熱擾動時，在Ve=0.8下，平板后表面溫度響應的數值解與解析解的對比.可以看出，數值解和解析解的誤差非常小，幾乎看不到差異，從而驗證了解析解的正確性.

圖1 平板前表面遭受突變熱擾動時后表面溫度響應的數值解與解析解的比較

圖2 平板前表面遭受突變熱擾動時不同熱松弛時間Ve下的表面溫度響應 (a)前表面溫度響應;(b)后表面溫度響應

圖2給出了平板前表面遭受突變熱擾動時不同無量綱熱松弛時間Ve下，平板兩表面無量綱溫度隨無量綱時間的變化曲線.可以看出當Ve=0.3，0.6，0.8時，其溫度分布曲線與典型的Fourier溫度分布曲線已不一致，尤其是當Ve=0.6，0.8時，其曲線有了凸凹點，熱傳導的非Fourier效應變得更加明顯.從圖2(b)可以看出其溫度響應曲線均存在一明顯的延遲，由于熱波的傳播速度為1/Ve，所以在平板后表面(無量綱化后X=1)，其延遲時間為Fo0=Ve.

4.2 簡諧變化邊界條件

當厚度為L的平板前表面遭受一幅值為q0，角頻率為α的簡諧熱擾動(q(t)=cos(αt))時

式中，Fo1=a/αL2.

把(41)式代入(34)和(35)式得平板前表面熱擾動簡諧變化時平板內部的溫度場分布

式中

對于Fourier導熱，當Ve→0時，把(41)式代入(34)和(37)式可得

使用(42)式，可以模擬得到厚度為L的平板在其前表面受到簡諧熱擾動時，平板前后兩表面的溫度響應.

圖3給出了平板前表面在簡諧熱流作用下，當Fo1=0.25，Ve=0.8時，平板前后兩表面的溫度響應曲線，反映出了非Fourier熱傳導的瞬態(tài)溫度特性.從圖3可以看出兩條曲線都存在一系列階躍點，它們表示溫度波波前經過邊界的傳播和反射到達的時刻.由于熱波的傳播速度為1/Ve，所以在兩表面X(X=0,1)處，階躍點位置為Fo=Ve·X，Ve(2+X)，Ve(4+X),···.由于擴散的作用，前表面溫度波的階躍值和幅值要比后表面的大.從圖3還可以看出溫度波曲線的階躍點隨著時間的增加而減小并逐漸消失，曲線最終變成光滑的周期曲線.

圖3 平板前表面遭受簡諧熱擾動時前后兩表面的溫度響應(Fo1=0.25，Ve=0.8)

圖4 平板前表面遭受簡諧熱擾動時不同熱松弛時間Ve下前后兩表面的溫度響應(Fo1=0.25) (a)前表面溫度響應;(b)后表面溫度響應

圖4給出了在前表面遭受簡諧熱擾動和Fo1=0.25的情況下，不同無量綱熱松弛時間Ve下，平板前后兩表面處無量綱溫度隨無量綱時間的變化曲線，以及采用(44)式得到的Fourier熱傳導模型下的溫度響應曲線.從圖中可以看出，隨著熱松弛時間Ve的減小，熱波的傳播速度增大，熱量能夠迅速地傳遞，從而導致平板內溫度響應的幅值也隨之減小，非Fourier效應逐漸減弱.Ve越小，非Fourier和Fourier的溫度響應曲線越接近.

4.3 任意周期邊界條件

當厚度為L的平板前表面遭受任意周期熱流變化時，假設該周期函數q0·q(t)的周期為2l.在實際問題中，q(t)只能在t≥0上有定義，故我們可以在t＜0的區(qū)間內將函數q(t)進行偶延拓，使q(t)=q(-t)，即延拓后的函數為偶函數.這樣周期函數q(t)可以展開成余弦級數的形式

當i=0時，方程(7)的解可以由(39)式得到：

把(50)與(52)式進行疊加，可得平板表面溫度任意周期變化時的非Fourier溫度場：

當Ve→0時，根據疊加原理與(40)，(44)和(45)式，可得在任意周期邊界條件下的非Fourier導熱溫度場：

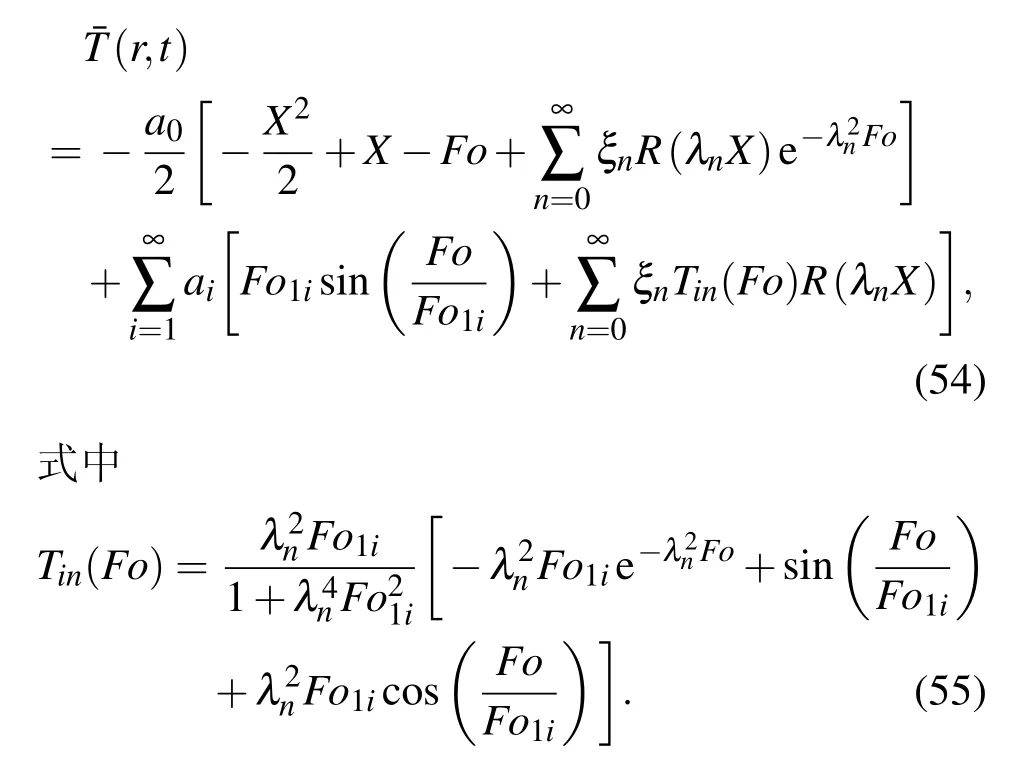
4.4 應用舉例

設q(t)是周期為2π的三角波函數(如圖5所示)，它在[0,2π)上的表達式為

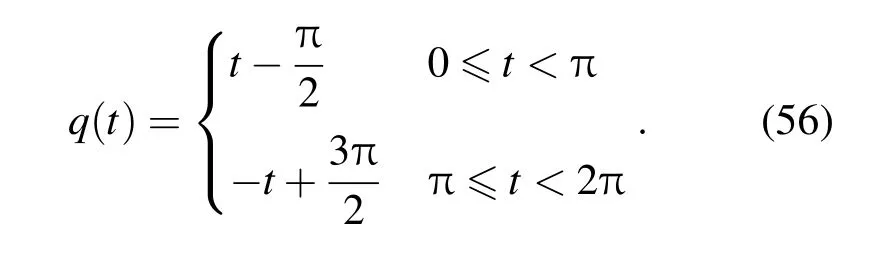
將函數q(t)進行偶延拓后，展開成余弦級數

將(57)式分別代入(53)式和(54)式得三角波條件下的非Fourier和Fourier導熱溫度場.

圖5 三角波熱擾動

圖6給出了在前表面遭受三角波熱擾動和a/L2=0.25的情況下，不同無量綱熱松弛時間Ve下，平板前后兩表面處無量綱溫度隨無量綱時間的變化曲線.從圖6可以看出，該溫度響應曲線除具有前面介紹的規(guī)律外，還具有隨著Ve的增大，特別是Ve=0.50時，溫度響應曲線形狀越接近前表面輸入的三角波熱擾動信號這樣的現象.這是因為，Ve越大，熱波的傳播速度越小，其延遲效應越明顯，隨著時間的增加，當階躍消失時，其溫度響應曲線形狀將越接近輸入信號.

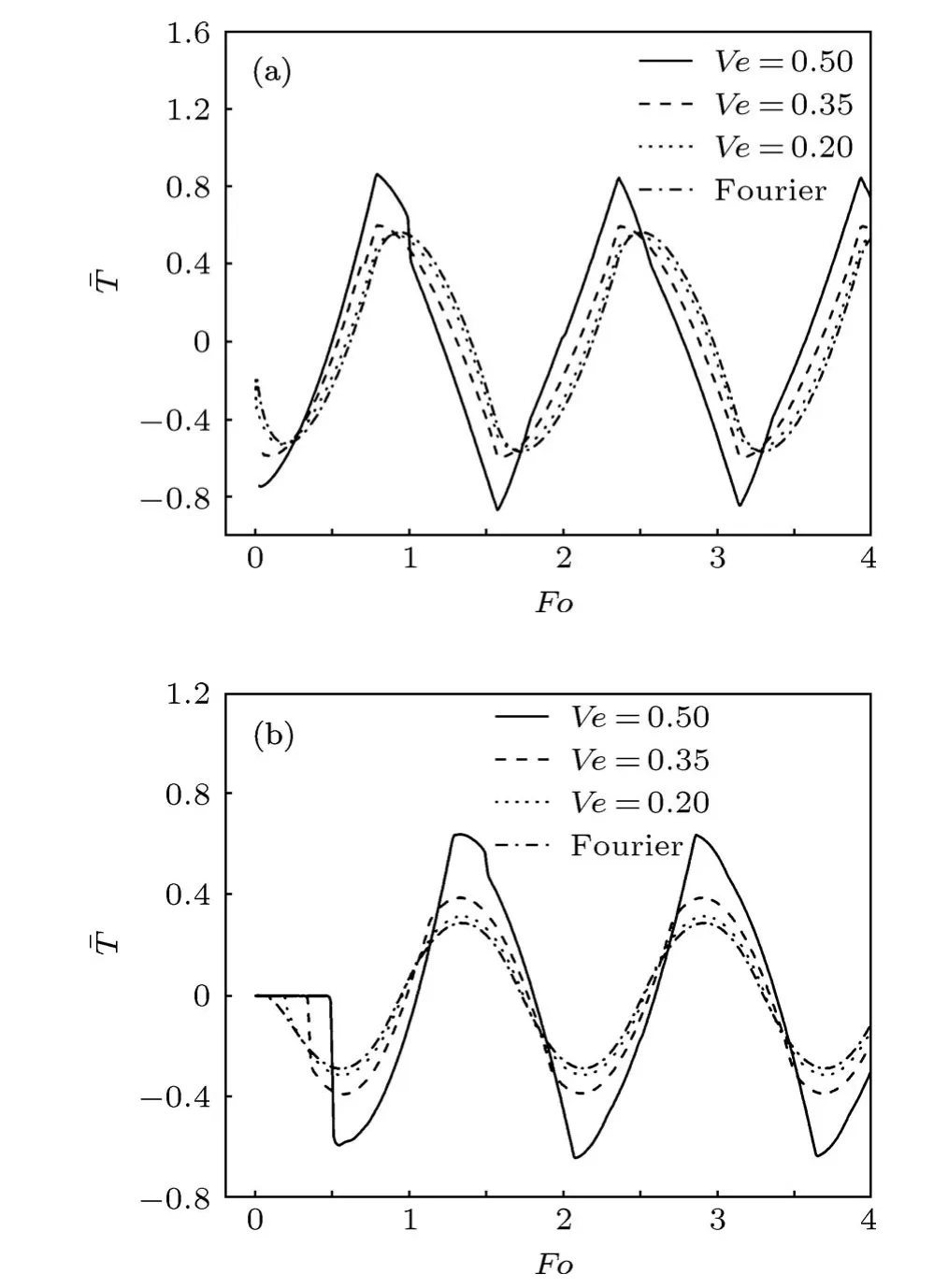
圖6 平板前表面遭受三角波熱擾動時不同熱松弛時間Ve下前后兩表面的溫度響應(a/L2=0.25) (a)前表面溫度響應;(b)后表面溫度響應

5 結論

本文首先通過分離變量法和Duhamel積分原理，對平板前表面遭受突變熱擾動和簡諧熱擾動這兩類邊界條件下的非Fourier熱傳導問題進行了分析求解，在此基礎上，利用Fourier級數展開法和疊加原理，得到了雙曲線型熱傳導方程在平板前表面遭受任意周期變化熱流時這個最一般情況下的解析解.通過理論計算與數值模擬，展示了非Fourier熱傳導模型所給出的溫度響應與Fourier熱傳導模型的如下差別：

1)溫度響應曲線存在一系列的階躍點，在兩表面X(X=0,1)處，它們依次出現的時間為Fo=Ve·X，Ve(2+X)，Ve(4+X)，···，但隨著時間的延長，溫度響應曲線逐漸變得光滑;

2)同一位置處，溫度響應的幅值隨著熱松弛時間Ve的減小而減小，最終趨近于Fourier熱傳導時的溫度響應幅值;

3)具有有限的傳播速度，其大小與1/Ve成線性關系;

4)熱松弛時間Ve越大，溫度響應曲線的形狀越和前表面遭受的熱流形狀相似.

[1]Wang Y Z，Song X N 2012Acta Phys.Sin.61 234601(in Chinese)[王穎澤，宋新南2012物理學報61 234601]

[2]Guo Z Y，Cao B Y 2008Acta Phys.Sin.57 4273(in Chinese)[過增元，曹炳陽2008物理學報57 4273]

[3]Tian X G，Shen Y P 2012Adv.Mech.42 18(in Chinese)[田曉耕，沈亞鵬2012力學進展42 18]

[4]Tung T L，Fong E 2011Int.J.Heat Mass Transfer54 4796

[5]Cattaneo C 1948Atti.Sem.Mat.Fis.Univ.Modena3 83

[6]Vernotte P 1958C.R.Acad.Sci.246 3154

[7]Tao Y J，Huai X L，Li Z G 2006Chin.Phys.Lett.23 2487

[8]Li S R，Zhou F X，Wu H M 2007Engineer.Mech.24 48(in Chinese)[李世榮，周鳳璽，吳紅梅2007工程力學24 48]

[9]Sarkar D，Haji-Sheikh A 2012Int.Commun.Heat Mass Transfer39 1009

[10]Tang D W，Araki N 1996Int.J.Heat Mass Transfer39 1585

[11]Moosaie A 2007Int.Commun.Heat Mass Transfer34 996

[12]Barletta A，Zanchini E 1997Heat and Mass Transfer32 285

[13]Ate fiG，Talaee M R 2011Arch.Appl.Mech.81 569

[14]Mishra S C，Sahai H 2012Int.J.Heat Mass Transfer55 7015

[15]Jiang F M 2006Heat and Mass Transfer42 1083

[16]Shirmohammadi R，Moosaie A 2009Int.Commun.Heat Mass Transfer36 827