三維柱腔內(nèi)輻射輸運(yùn)的一維模擬

宋天明 楊家敏

(中國(guó)工程物理研究院激光聚變研究中心，綿陽(yáng) 621900)

(2012年5月27日收到;2012年7月16日收到修改稿)

1 引言

在慣性約束聚變、輻射輸運(yùn)、輻射流體力學(xué)等物理實(shí)驗(yàn)中，使用強(qiáng)激光產(chǎn)生的X射線(xiàn)輻射源對(duì)柱腔約束下的樣品進(jìn)行加熱，以研究X射線(xiàn)輻射在不同介質(zhì)中傳輸?shù)奶匦砸约皩?duì)輻射能譜的改造[1-6].為了對(duì)這一物理過(guò)程進(jìn)行模擬，國(guó)內(nèi)外開(kāi)發(fā)了很多輻射流體力學(xué)模擬程序，包括一維模擬程序如MULTI[7]、RDMG[8]等，二維程序如LARED[9]、LASNEX[10]等，三維程序如 Hydra[11]等.一維模擬程序一般模型簡(jiǎn)單，運(yùn)行時(shí)間較短.而二維和三維程序往往需要耗費(fèi)較多的計(jì)算資源并且需要運(yùn)行較長(zhǎng)時(shí)間.因此，經(jīng)常將實(shí)驗(yàn)相關(guān)的物理問(wèn)題簡(jiǎn)化為一維模型進(jìn)行理論分析.而輻射在柱腔中輸運(yùn)的過(guò)程中，腔壁被燒蝕，損失了輻射能量;或者由于管壁上的診斷口造成了輻射的直接漏失.由于涉及輻射與管壁作用的物理過(guò)程或靶的三維空間結(jié)構(gòu)，無(wú)法直接使用一維模擬程序進(jìn)行模擬.由于沒(méi)有考慮二維或三維因素的影響，一維模擬會(huì)給計(jì)算結(jié)果帶來(lái)較大誤差[1].

本文首先介紹了針對(duì)一維模擬無(wú)法處理的邊緣漏失對(duì)一維輻射流體力學(xué)程序MULTI的修正;然后，用修正后的程序?qū)鼙诘入x子體運(yùn)動(dòng)實(shí)驗(yàn)中X射線(xiàn)輻照產(chǎn)生的金等離子體的界面運(yùn)動(dòng)軌跡進(jìn)行了模擬;最后對(duì)程序修正的效果進(jìn)行了總結(jié)和討論.

2 輻射輸運(yùn)計(jì)算的修正

MULTI[7]是一維拉格朗日輻射流體力學(xué)模擬，程序能夠進(jìn)行多群輻射輸運(yùn)的計(jì)算.程序使用的不透明度數(shù)據(jù)用SNOP計(jì)算，狀態(tài)方程則使用MPQeos程序的QEOS模型[12]計(jì)算，數(shù)據(jù)存儲(chǔ)在SESAME格式的數(shù)據(jù)表格中，計(jì)算時(shí)可實(shí)時(shí)調(diào)用.

在一維輻射輸運(yùn)的數(shù)值模擬中，一個(gè)網(wǎng)格單元中的輻射輸運(yùn)如圖1所示.

輻射流從左側(cè)進(jìn)入界面1，與網(wǎng)格內(nèi)物質(zhì)相互作用后從界面2流出，進(jìn)入下一個(gè)網(wǎng)格.在三維空間中，定義F12為從界面1輸運(yùn)到界面2的輻射流份額，它由視角因子決定.對(duì)柱腔來(lái)說(shuō)，從圓柱體一個(gè)圓面到另一個(gè)圓面的視角因子有解析解.假設(shè)圓柱腔半徑為r，網(wǎng)格寬度為a，定義X=2+a2/r2，那么兩個(gè)端面間的視角因子為假設(shè)在一個(gè)網(wǎng)格內(nèi)物質(zhì)是光學(xué)薄的，那么從界面1進(jìn)入網(wǎng)格并與管壁作用的輻射流份額為(1-F12).定義反照率α為再發(fā)射輻射流與入射輻射流的比值，那么將有份額flost=(1-F12)(1-α)的輻射能流會(huì)在與管壁的相互作用中損失.部分靶型為了完成測(cè)量而在輸運(yùn)管壁上開(kāi)了診斷口，輸運(yùn)管內(nèi)的部分輻射通過(guò)診斷口完全漏失到管外，定義這個(gè)份額為f，損失輻射的總份額為

那么除去管壁和診斷口帶來(lái)的輻射能量損失，剩余的1-flost將參與到與介質(zhì)的相互作用并進(jìn)入到下一個(gè)網(wǎng)格中，繼續(xù)輻射輸運(yùn)過(guò)程.(1)式中，反照率α可以使用定標(biāo)率公式來(lái)模擬計(jì)算，診斷口引起的輻射能量損失份額f根據(jù)診斷口所占管壁的面積比來(lái)計(jì)算.

圖1 模擬網(wǎng)格示意圖

3 模擬算例

下面用一個(gè)實(shí)驗(yàn)算例來(lái)對(duì)計(jì)算程序的修正進(jìn)行檢驗(yàn).Yang等[1]在神光II激光裝置上進(jìn)行了研究金壁等離子體運(yùn)動(dòng)的實(shí)驗(yàn)，如圖2所示.實(shí)驗(yàn)中利用1 ns方波激光脈沖單端注入半黑腔產(chǎn)生的強(qiáng)X射線(xiàn)作為輻射源，X射線(xiàn)從半腔靶底部進(jìn)入輸運(yùn)柱腔.半腔靶底部為防止散射激光直接加熱樣品，安裝了0.1μm的金膜和1μm的CH膜.安裝在半腔靶底部的金柱腔中填充CH泡沫，在柱腔的底部有金平面靶，X射線(xiàn)輻射輸運(yùn)到金平面靶后對(duì)其進(jìn)行燒蝕，產(chǎn)生向泡沫中運(yùn)動(dòng)的金等離子體.通過(guò)在柱腔上開(kāi)診斷口的方式，使用Ti盤(pán)靶產(chǎn)生的He-α線(xiàn)發(fā)射作為背光源，用X射線(xiàn)條紋相機(jī)對(duì)金等離子體的運(yùn)動(dòng)軌跡進(jìn)行記錄.

實(shí)驗(yàn)中還使用軟X光能譜儀從激光注入口與黑腔對(duì)稱(chēng)軸呈30°方向觀測(cè)半黑腔內(nèi)的輻射溫度，測(cè)量的輻射溫度如圖3.數(shù)值模擬中以軟X光能譜儀測(cè)量的輻射溫度時(shí)間演化過(guò)程為輸入條件，直接模擬輻射在泡沫填充的輸運(yùn)管中的傳輸和與金平面靶的相互作用.

通過(guò)背光照相，用條紋相機(jī)測(cè)得了金等離子體運(yùn)動(dòng)的軌跡，實(shí)驗(yàn)數(shù)據(jù)如圖4.去掉初始加速階段，對(duì)線(xiàn)性運(yùn)動(dòng)階段的界面數(shù)據(jù)進(jìn)行線(xiàn)性擬合，得到等離子體界面運(yùn)動(dòng)速度約為37.5 m/s.

圖2 管壁等離子體運(yùn)動(dòng)實(shí)驗(yàn)示意圖

圖3 黑腔內(nèi)輻射溫度隨時(shí)間的演化

圖4 實(shí)驗(yàn)測(cè)量的等離子體界面位置和擬合曲線(xiàn)

Yang等使用一維輻射流體力學(xué)模擬程序RTMG以及二維輻射輸運(yùn)模擬程序LARED-R進(jìn)行了模擬計(jì)算.結(jié)果顯示，一維程序由于沒(méi)有考慮管壁漏失等邊緣效應(yīng)，模擬結(jié)果與實(shí)際不符，而二維輻射輸運(yùn)模擬結(jié)果更接近實(shí)測(cè)結(jié)果[1].我們使用一維MULTI程序?qū)鼙谶\(yùn)動(dòng)進(jìn)行模擬，考慮金和CH膜以及柱腔中填充的泡沫和金平面靶四層材料，用軟X光能譜儀測(cè)得的輻射流作為輻射源.不考慮管壁反照和漏失，那么金等離子體向上運(yùn)動(dòng)的速度約為58.6 km/s.這個(gè)數(shù)值與實(shí)驗(yàn)結(jié)果相差較大，因此必須考慮管壁反照和漏失的影響.實(shí)驗(yàn)中使用的靶型除了存在管壁吸收帶來(lái)的輻射能量損失外，管壁上還開(kāi)有兩個(gè)診斷口，這使得管靶不是軸對(duì)稱(chēng)，而是三維的.使用本文介紹的方法，金壁的反照率使用α=(1+0.32T-0.7t-0.38)-1[13]，根據(jù)診斷口在管壁上所占空間比例計(jì)算經(jīng)過(guò)柱腔壁上的開(kāi)口的漏失約為15.6%.通過(guò)模擬計(jì)算得到的金等離子體界面運(yùn)動(dòng)速度約為38 km/s.數(shù)值模擬和實(shí)驗(yàn)測(cè)量得到的金等離子體界面運(yùn)動(dòng)軌跡見(jiàn)圖5.可見(jiàn)，通過(guò)添加輻射能量損失等邊緣效應(yīng)對(duì)輸運(yùn)計(jì)算進(jìn)行修正，模擬得到的金等離子體界面運(yùn)動(dòng)軌跡和實(shí)驗(yàn)測(cè)量的結(jié)果符合較好;圖中還給出了LARED-R二維程序模擬的結(jié)果.

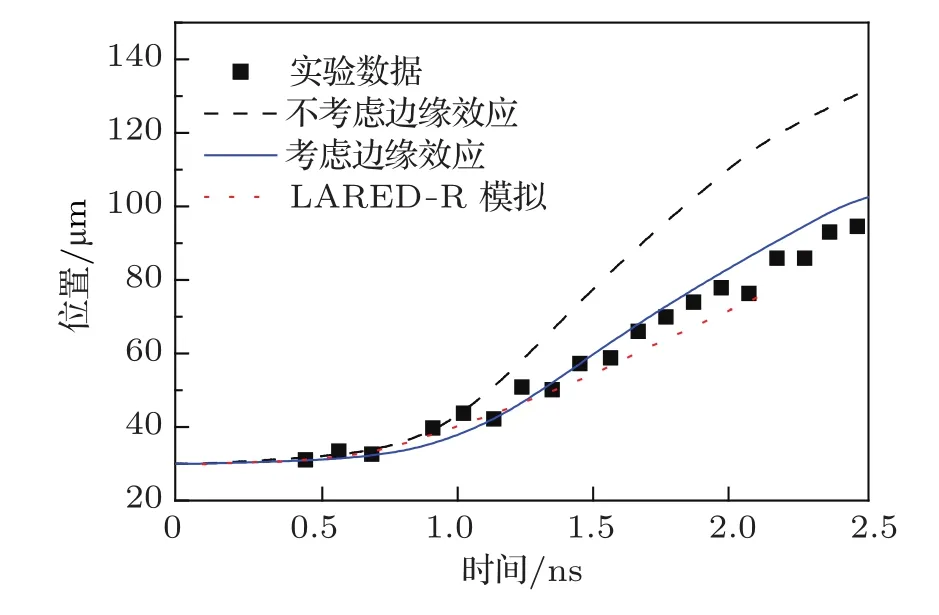
圖5 MULTI修正前后的模擬結(jié)果

從圖5中還可以看到，模擬結(jié)果和實(shí)驗(yàn)測(cè)量結(jié)果仍有一些差異.除了程序數(shù)值模擬受網(wǎng)格劃分、不透明度等參數(shù)誤差的影響之外，二者的誤差還包括：上述模型中只考慮了輻射的漏失和損失，沒(méi)有考慮流體運(yùn)動(dòng)受管壁的影響所產(chǎn)生的二維效應(yīng)(本算例中管子的長(zhǎng)徑比較小，這一項(xiàng)影響較小);另外實(shí)驗(yàn)測(cè)量中金等離子膨脹時(shí)存在密度變化，實(shí)驗(yàn)數(shù)據(jù)處理時(shí)界面的提取也存在誤差，等等.

4 結(jié)論

通過(guò)對(duì)一維輻射流體力學(xué)程序的改進(jìn)，使用視角因子和反照率定標(biāo)公式將管壁上的輻射能量損失等邊緣效應(yīng)考慮到一維輻射輸運(yùn)模擬中，使一維程序能夠?qū)ΧS或三維柱腔輻射的漏失進(jìn)行模擬計(jì)算.對(duì)管壁等離子體運(yùn)動(dòng)實(shí)驗(yàn)中一個(gè)有診斷口的柱腔靶的模擬，成功將診斷口漏失和管壁吸收的輻射能損失考慮進(jìn)來(lái)，得到了和實(shí)驗(yàn)測(cè)量結(jié)果相近的金等離子體界面運(yùn)動(dòng)軌跡.

數(shù)值實(shí)驗(yàn)證明，通過(guò)視角因子和反照率定標(biāo)公式將管壁漏失添加到輻射輸運(yùn)中能夠在一維模擬程序中反映簡(jiǎn)單二維或三維空間中的一些物理現(xiàn)象，因而可以快速實(shí)現(xiàn)對(duì)某些三維輻射輸運(yùn)問(wèn)題的近似模擬.用快捷的一維模擬計(jì)算確定了關(guān)鍵參數(shù)范圍后再使用需要較多計(jì)算資源和計(jì)算時(shí)間的二維、三維等更復(fù)雜模擬程序進(jìn)行更深入準(zhǔn)確的計(jì)算，可以有效節(jié)約計(jì)算資源，方便我們對(duì)這些物理現(xiàn)象的研究.

[1］Yang J，Meng G，Zhu T，Zhang J，Li J，He X，Yi R，Xu Y，Hu Z，Ding Y，Liu S，Ding Y 2010Phys.Plasmas17 1

[2］Back C A，Bauer J D，Hammer J H，Lasinski B F，Turner R E，Rambo P W，Landen O L，Suter L J，Rosen M D，Hsing W W 2000Phys.Plasmas7 2126

[3］Back C A，Bauer J D，Landen O L，Turner R E，Lasinski B F，Hammer J H，Rosen M D，Suter L J，Hsing W H 2000Phys.Rev.Lett.84 274

[4］Jiang S E，Xu Y，Ding Y K，Lai D X，Zheng Z J，Sun K X，Huang Y X，Hu X，Yi R Q，Cui Y L 2005Sci.ChinaGPhysics Mechanics&Astronomy35 473(in Chinese)[江少恩，許琰，丁永坤，賴(lài)東顯，鄭志堅(jiān)，孫可煦，黃翼翔，胡昕，易榮清，崔延莉2005中國(guó)科學(xué)G輯物理學(xué)力學(xué)天文學(xué)35 473］

[5］Jiang S E，Sun K X，Huang T X，Cheng J X，Ding Y K，Hu X，Cui Y L，Chen J S，Yu Y N，Zheng Z J 2004Acta Phys.Sin.53 1425(in Chinese)[江少恩，孫可煦，黃天暄，成金秀，丁永坤，胡昕，崔延莉，陳久森，于艷寧，鄭志堅(jiān)2004物理學(xué)報(bào)53 1425］

[6］Cheng J X，Miu W Y，Sun K X，Wang H B，Yang J M，Cao L F，Wen T S，Chen Z L，Yang C B，Jiang S E，Cui Y L，Tang X Q，Yu Y N，Chen J S 2000Acta Phys.Sin.49 282(in Chinese)[成金秀，繆文勇，孫可熙，王紅斌，楊家敏，曹磊峰，溫天舒，陳正林，楊存榜，江少恩，崔延莉，湯小青，于艷寧，陳久森2000物理學(xué)報(bào)49 282］

[7］Ramis R，Schmalz R，Meyer-ter-Vehn J 1988Comput.Phys.Commun.49 475

[8］Gu P J，Pei W B，F(xiàn)eng T G，Wa C S 2005Sci.ChinaGPhysics,Mechanics&Astronomy48 345

[9］Zhu S P，Zhang W Y 2006Journal of the Korean Physical Society49 33

[10］Harte J A，Alley W E，Bailey D S，Eddleman J L，Zimmerman G B 1997 1996Lawrence Livermore National Laboratory ICF Annual ReportUCRL-LR-105821-96 150

[11］Marinak M M，Kerbel G D，Gentile N A，Jones O，Munro D，Pollaine S，Dittrich T R，Haan S W 2001Phys.Plasmas8 2275

[12］More R M，Warren K H，Young D A，Zimmerman G B 1988Phys.Fluids31 3059

[13］Lindl J，1995Phys.Plasmas2 3933