基于最短距離優(yōu)先的集裝箱空箱調(diào)度優(yōu)化算法
田昌彪, 王曉峰
(上海海事大學(xué) 信息工程學(xué)院,上海 201306)
0 引 言
由于集裝箱具有運輸量大、便于機械化操作、能減少物品破損等優(yōu)點,世界海運貨物的集裝箱化已成為不可阻擋的發(fā)展趨勢.然而由于國際貿(mào)易不平衡及集裝箱管理等方面的原因,每天都有大量的集裝箱空箱由箱源充裕地區(qū)運往箱源匱乏地區(qū),隨即產(chǎn)生集裝箱空箱調(diào)運問題.
對經(jīng)濟危機下的船公司來講,一個好的空箱調(diào)度算法不僅能降低成本、提高經(jīng)濟效益,而且能提高運輸設(shè)備的利用率、改善服務(wù)質(zhì)量.同時,空箱最優(yōu)化問題的本身就是對資源的最優(yōu)化配置,解決一類問題,就可以解決很大一部分相似資源的最優(yōu)化配置問題.
國內(nèi)外學(xué)者對空箱調(diào)度問題進行大量研究,取得一系列成果,為實際運營過程提供有益的參考.施欣[1-2]對海上集裝箱空箱調(diào)運過程進行分析,建立系統(tǒng)優(yōu)化模型;劉恒江[3-4]把航線經(jīng)營人作為主體,建立空箱調(diào)運的Petri網(wǎng)模型;周紅梅等[5]借鑒鐵路空車調(diào)度優(yōu)化模型,建立海運空箱調(diào)運優(yōu)化模型;劉建軍等[6]基于廣義費用目標(biāo)函數(shù)提出從港口到貨主企業(yè)間不同運輸方式的集裝箱組織優(yōu)化模型.武振業(yè)等[7]建立需求不確定的海運集裝箱路徑隨機規(guī)劃模型.國外研究方面,F(xiàn)LOREZ[8]建立利潤優(yōu)化模型研究遠洋航運企業(yè)空箱租賃和重新配置問題;SHEN等[9]構(gòu)建海運空箱調(diào)運決策支持系統(tǒng);WHITE等[10]通過構(gòu)造一個空間-時間模型描述現(xiàn)實中的集裝箱空箱調(diào)運問題;CHOONG等[11]建立以美國五大湖區(qū)為實際調(diào)運背景的空箱多式聯(lián)運調(diào)運整數(shù)規(guī)劃模型,分析規(guī)劃周期長短對多式聯(lián)運中空箱管理的影響;JULA等[12]建立線性規(guī)劃模型解決洛杉磯/長灘復(fù)合港的交通擁擠問題,并提出線性規(guī)劃問題的求解方法和優(yōu)化解.然而這些研究在建立模型時進行大量假設(shè),與實際系統(tǒng)相差較遠.本文擬在考慮多箱種的情況下,結(jié)合大型船公司的實際情況,提出新的空箱調(diào)度優(yōu)化算法,并運用實驗進行驗證.
1 建立模型
1.1 模型假定
假定港口運輸網(wǎng)絡(luò)中一共有U個港口,其中m個港口多余空箱,n個港口缺少空箱.模型用到的變量:設(shè)X(k,i,j,t)表示時刻t空箱經(jīng)船k由多箱港口i調(diào)往缺箱港口j的空箱量,其中,k=1,2,…,K,i=1,2,…,U,j=1,2,…,U,t=1,2,…,T;T(k,i,j,t)表示時刻t空箱經(jīng)船k由多箱港口i調(diào)往缺箱港口j的時間;D(k,i,j,t)表示時刻t經(jīng)船k由多箱港口i調(diào)往缺箱港口j的距離;Z(k,i,j,t)表示時刻t經(jīng)船k從港口i運往港口j的重箱量;O(i,t)表示租箱量;Q(i,t)表示空箱存量;Ti(i,t)表示堆場存放時間;Tr(i,t)表示租箱時間.
模型用到的參數(shù):C(k,i,j,t)表示時刻t經(jīng)船k由多箱港口i調(diào)往缺箱港口j的單位空箱單位距離運輸成本;Y(k,i)表示船k運輸能力限制;Ch(i,t)表示單位空箱裝卸成本;Cr(i,t)表示單位空箱單位時間的租箱費率;Ci(i,t)表示單位空箱單位時間的存箱成本;T表示整個空箱調(diào)度的周期,為常數(shù);K表示船舶數(shù)量;N表示箱型數(shù)量.
1.2 數(shù)學(xué)模型
空箱調(diào)度成本一般包括牽引成本、維修成本、管理成本、托運成本、空箱裝卸成本、運輸成本、堆場成本、租箱成本等.為簡化模型,只考慮空箱裝卸成本、運輸成本、堆場成本、租箱成本.
空箱裝卸成本=調(diào)箱量×單位空箱裝卸成本=
(1)
運輸成本=調(diào)箱量×經(jīng)過的距離×單位空箱單位距離運輸成本=
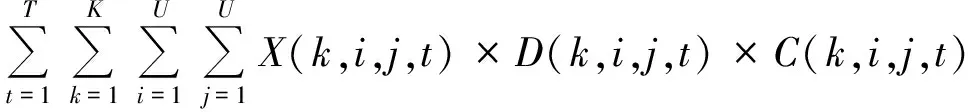
(2)
堆場成本=空箱存量×單位空箱單位時間的堆場成本×堆場存放時間=
(3)
(4)
因此,航線成本最小化的目標(biāo)函數(shù)為
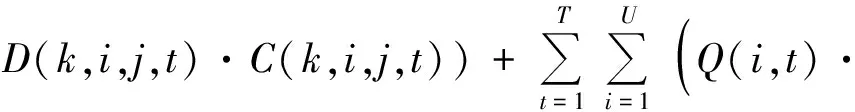
(5)
判定某一確定缺箱港口與某一確定多箱港口之間選擇空箱調(diào)度的方法:單位空箱裝卸成本+單位空箱調(diào)運成本+單位空箱堆場成本<單位租箱成本,則調(diào)箱,即
Ch(i,t)+D(k,i,j,t)·C(k,i,j,t)+
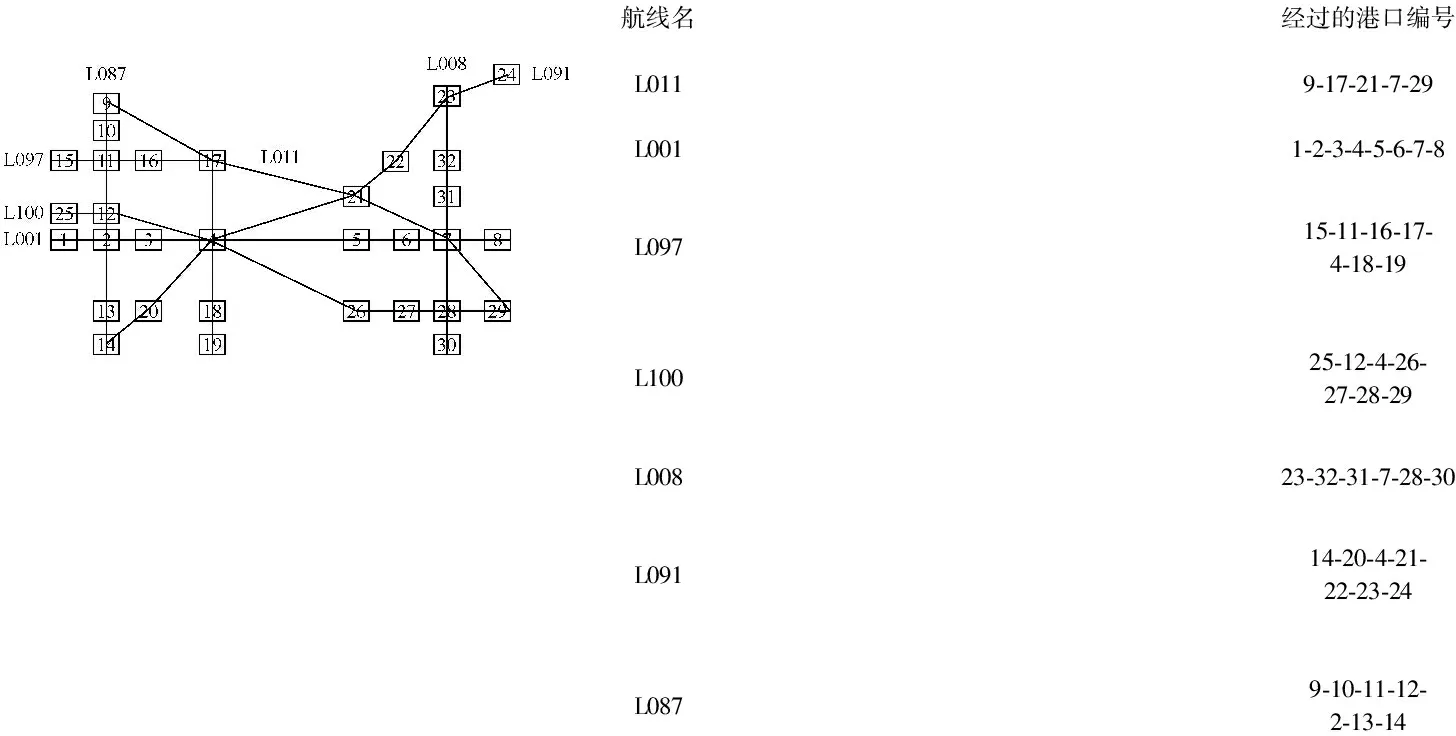
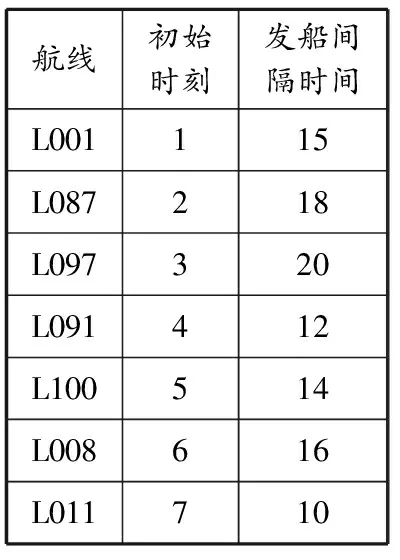
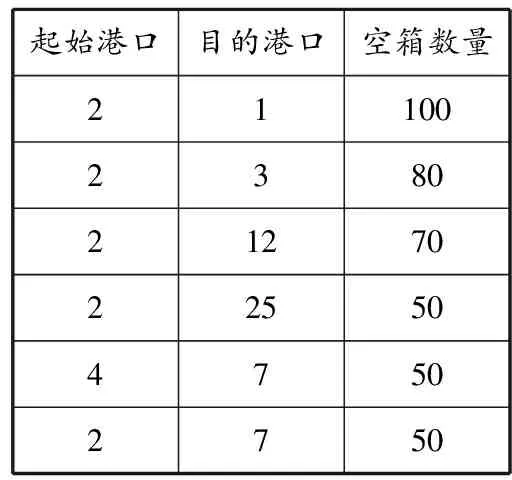
Ci(i,t)·Ti(i,t) 約束函數(shù)為 X(k,i,j,t)+Z(k,i,j,t)≤Y(k,i)[13] (6) T(k,i,j,t)+Ti(i,t)≤T (7) (8) 式(6)表示空箱量和重箱量應(yīng)小于船舶的最大裝載量;式(7)表示空箱調(diào)運時間和占用堆場時間之和在調(diào)度期限之內(nèi);式(8)表示空箱調(diào)運量小于空箱的總存量. 國內(nèi)大型船公司的箱管部門一般按照人工經(jīng)驗[14]調(diào)度空箱,目前以最短距離優(yōu)先調(diào)度為主,即把多余的空箱運輸?shù)骄嚯x最近的缺箱港口,從而實現(xiàn)時間最少、距離最短,達到節(jié)約成本的目的. 距離是指兩物體在空間或時間上相隔的長度.最短距離優(yōu)先是指在空箱調(diào)度過程中總是優(yōu)先調(diào)度距離缺箱港口最近的多箱港口的空箱.距離最近的兩個港口之間實現(xiàn)空箱最優(yōu)調(diào)度,不僅能減少運輸成本和運輸時間,還能有效提高運營效率. 將任意兩港口之間的實際距離表示成矩陣,調(diào)度時只需在距離最近的兩個港口之間進行按需分配即可實現(xiàn)最短距離優(yōu)先調(diào)度.為敘述方便,給出32個港口的分布,見圖1. 圖1港口分布網(wǎng)絡(luò) 為實現(xiàn)空箱調(diào)度成本的最低化,需要已知各港口之間的距離和各個港口對應(yīng)空箱箱型的數(shù)量. 式中:dij表示港口i與港口j之間的距離,1≤i,j≤v. 式中:aij表示港口i,箱型為j的集裝箱空箱數(shù)量(1≤i≤v,1≤j≤N),正負分別表示可供應(yīng)或需求的空箱數(shù)目,0表示不缺少也不多余,但并不代表該港口一個空箱都沒有,只表示該港口空箱只能滿足自身的需要而且不能提供多余的空箱.假設(shè)f表示空箱最短距離優(yōu)先調(diào)運函數(shù),其中有2個參數(shù)D和A.{aij|i=1,2,…,v}表示各港口某一箱型j的空箱數(shù)量,數(shù)組S存儲多箱港口的編號,數(shù)組E存儲缺箱港口的編號,s表示多箱港口編號,e表示缺箱港口編號,算法步驟如下: 步驟1將箱型為1的各港口的空箱數(shù)量存入{ai1}數(shù)組. 步驟2將{ai1}中大于0的港口編號存入數(shù)組S,小于0的港口編號存入數(shù)組E. 步驟3找出{dij|i∈S,j∈E}的最小值,并把多箱港口編號賦值給s,缺箱港口編號賦值給e. 步驟4判斷as1和ae1絕對值的大小,修改{ai1},打印出s,e,該箱型空箱的數(shù)目. 步驟5判斷數(shù)組S或E是否為空.若否,則執(zhí)行步驟2;若是,跳出循環(huán),執(zhí)行步驟6. 步驟6將箱型加1,執(zhí)行循環(huán),直至N. 空間距離最短的兩個港口之間往往有很多條路徑,要求得成本最低的路徑,需要窮舉路徑,從中擇優(yōu).實際最短距離路徑有時未必是最優(yōu)路徑,成本最低的路徑才是最優(yōu)路徑,因此需要窮舉路徑以決定空箱調(diào)度方案.若圖1中的2號港口多余很多空箱,4號缺少很多空箱,而且也滿足最短距離的條件,但如果2號港口常年出口貨物到4號港口,這時2號港口的空箱通過L001航線運輸?shù)?號港口就會大大增加成本,而一般的解決辦法就是窮舉路徑.2號港口到4號港口的直達線路L001成本高,就可以取2號港口運輸?shù)?2號港口、12號港口運輸?shù)?號港口的路徑,或是其他的窮舉出來的成本更低的路徑. 盡管空箱調(diào)度一般需要幾次中轉(zhuǎn)才能到達目的港口,但也是有限制的.隨著中轉(zhuǎn)港口增多,中轉(zhuǎn)過程的裝卸費用、運輸成本會大大增加.一般中轉(zhuǎn)次數(shù)不超過一個固定的常數(shù).此處只給出中轉(zhuǎn)3次以內(nèi)的窮舉路徑算法.設(shè)F表示窮舉路徑函數(shù),其中有3個參數(shù):多箱港口編號s,缺箱港口編號e,航線L;m1表示中轉(zhuǎn)港口編號,m2表示另一中轉(zhuǎn)港口編號.具體算法如下. 步驟1判斷港口s和e是否在同一航線上.是則執(zhí)行步驟2,否則執(zhí)行步驟3. 步驟2查航線表L,將港口s與e之間的時間和距離累加.根據(jù)距離計算運輸費用,裝卸費用按1次計算,堆場費用為0,租箱費用已知,生成結(jié)果集. 步驟3在港口s所在的航線上找中轉(zhuǎn)港口m1及m1所在的航線,判斷m1與e是否在同一航線上.是則執(zhí)行步驟4,否則執(zhí)行步驟5. 步驟4分別查航線表,將港口s與m1,m1與e之間的時間和距離累加.根據(jù)距離計算運輸費用,裝卸費用按2次計算,按航期表計算堆場時間,得出堆場費用,租箱費用已知,生成結(jié)果集. 步驟5在m1所在的航線上再找一中轉(zhuǎn)港口m2及m2所在的航線,判斷m2與e是否在同一航線上,是則執(zhí)行步驟6,否則放棄. 步驟6分別查航線表,將s與m1,m1與m2,m2與e之間的時間和距離累加.根據(jù)距離計算運輸費用,裝卸費用按3次計算,按航期表計算堆場時間,得出堆場費用,租箱費用已知,生成結(jié)果集. 步驟7將結(jié)果集按成本進行排序并輸出. 對于某一固定的班輪,基本上有固定的掛靠時刻和掛靠港口,用一個固定的航期表表示.船期表中所列項目包括港口編號、上一港口到下一港口的時間和距離. 假定A和B是同一時刻某航線上兩端的港口,i和j表示需要進行空箱調(diào)度的兩個港口,i表示起始港口,j表示終點港口,若A→B,B→A方向上各有一班輪,設(shè)初始時刻為0,班輪周期為T1.用tij表示i到j(luò)所用的時間. (1)如果i和j都在AB航線上,則:A→B方向,船舶到i的所有時刻ti=tAi+K1T1,K1=0,1,2,…;B→A方向,船舶到i的所有時刻ti=tBi+K1T1,K1=0,1,2,….查船期表,將時間字段和距離字段相加可得i到j(luò)所需要的總時間tij和總距離,由于不經(jīng)過中轉(zhuǎn),堆場時間為0,把完整的裝一次、卸一次看作裝卸一次,用成本分析就可算得裝卸成本、運輸成本、堆場成本.配船方案為AB航線的(K1+1)航次. (2)如果i和j不在同一航線上,并且兩航線有共同港口M,i在AB航線上,j在CD航線上,且初始時刻都為0,AB航線的周期為T1,CD航線的周期為T2,則:A→B方向,船舶到i的所有時刻ti=tAi+K1T1,K1=0,1,2,…;C→D方向,船舶到j(luò)的所有時刻tj=tCj+K2T2,K2=0,1,2,…;由i到j(luò)所需要的時間t=tj-ti=tCj-tAi+K2T2-K1T1.船舶運輸時間tiM+tMj.堆場堆放時間tAM+K2T2-tCM-K1T1(≥0).配船方案為AB航線的(K1+1)航次,和CD航線的(K2+1)航次. 表1 各航線的船期表 假定一個有32個港口、7條航線的港口運輸網(wǎng)絡(luò),見圖1.對某一特定類型的空箱,1號港口缺少100個,2號港口多余400個,3號港口缺少100個,4號港口多余50個,7號港口缺少100個,12號港口缺少80個,25號港口缺少70個,其他港口空箱數(shù)目為0.其中部分航線的船期見表1. 為簡述方便,中轉(zhuǎn)費用常數(shù)假定為4,單位距離運輸費用為5,單位空箱單位時間堆場費用為1,租箱費用為65. 表2 最短距離優(yōu)先調(diào)度結(jié)果 第一步給出以最短距離優(yōu)先的某一箱型的調(diào)度結(jié)果,包括起始港口和目的港口及需運輸?shù)目障鋽?shù)量,見表2. 確定起始港口為2號港口、目的港口為7號港口后,計算出排序后2號港口到7號港口的窮舉3次中轉(zhuǎn)限制內(nèi)的路徑結(jié)果集合,見表3. 當(dāng)單位租箱成本小于單位空箱調(diào)度成本時,選擇租箱,否則選擇空箱調(diào)度.如,表5中第1條路徑空箱調(diào)度比較劃算,而其他7條選擇租箱比較劃算. 與以人工經(jīng)驗調(diào)度為主的空箱調(diào)度比較,該算法按距離遠近給出調(diào)度先后順序,能有效給出空箱調(diào)度優(yōu)化路徑,并按成本大小排序,同時對是否租箱給出輔助決策. 結(jié)果不僅可以按照成本排序,還可以按照時間進行排序,得出空箱調(diào)運最短時間調(diào)運方案. 由于空箱調(diào)運系統(tǒng)復(fù)雜,根據(jù)單一的排序后的成本或時間空箱調(diào)運方案,并不能得出最優(yōu)方案,二者不可兼得,最終還需要箱管部門結(jié)合其他因素制訂空箱調(diào)度計劃. 該空箱調(diào)度算法不僅能有效給出空箱調(diào)度最優(yōu)路徑,而且對是否租箱給出輔助決策,使空箱調(diào)度變得有章可循.與實際人工經(jīng)驗調(diào)度比較,該算法能簡化調(diào)度過程、提高調(diào)度效率. 該算法適用于航線較多的情況,但對實際中特定的情況并不適用.比如,對于同樣是出口為主的港口上海港和寧波港,基本上沒有空箱調(diào)運,該方法失效.為更好地應(yīng)用,還需要進一步改進算法. 表3 窮舉3次中轉(zhuǎn)限制內(nèi)的路徑結(jié)果 參考文獻: [1] 施欣. 集裝箱海運空箱調(diào)運優(yōu)化分析[J]. 系統(tǒng)工程理論與實踐, 2003, 4(4): 70-76. [2] 施欣. 基于Petri網(wǎng)的航運業(yè)務(wù)流程的仿真優(yōu)化[J]. 系統(tǒng)仿真學(xué)報, 2001, 11(6): 767-780. [3] 劉恒江. 集裝箱空箱調(diào)運分析[J]. 集裝箱化, 2001, 12(10): 11-13 [4] 劉恒江. 集裝箱空箱調(diào)運Petri網(wǎng)模型仿真分析[D]. 上海: 上海海運學(xué)院, 2002. [5] 周紅梅, 方芳. 航運集裝箱空箱調(diào)運優(yōu)化模型的研究[J]. 武漢理工大學(xué)學(xué)報: 交通科學(xué)與工程版, 2003(3): 384-387. [6] 劉建軍, 楊浩. 港口樞紐集裝箱運輸?shù)慕M織優(yōu)化研究[J]. 土木工程學(xué)報, 2004, 37(10): 99-103. [7] 武振業(yè), 宋天生, 趙柯. 海運集裝箱運輸路徑選擇[J]. 西南交通大學(xué)學(xué)報, 2006, 41(3): 269-272. [8] FLOREZ H. Empty container repositioning and leasing:an optimization model[D]. New York: Polytechnic Institute of New York, 1986. [9] SHEN W S, KHONG C M. A DSS for empty container distribution planning[J]. Decision Support System, 1955, 15(1): 75-82. [10] WHITE W W,BOMBERAWLT A M. A network algorithm for empty freight car allocation[J]. IBM System J, 1969, 15(2): 147-169. [11] CHOONG S T, COLE M H, KUTANOGLU E. Empty container management for intermodal transportation networks[J]. Transportation Res Part E: Logistics & Transportation Rev, 2002, 38(6): 423-438. [12] JULA H, CHASSIAKOS A, IOANNOU P. Port dynamic empty container reuse[J]. Transportation Res Part E: Logistics & Transportation Rev, 2006, 42(1): 43-60. [13] 劉大镕, 賀斌, 蔣良奎, 等. 隨機(單箱種)陸上空箱調(diào)運模型[J]. 上海海運學(xué)院學(xué)報, 2000, 21(3): 8-18. [14] 楊洋. 班輪公司空箱合作調(diào)運優(yōu)化模型[J]. 上海海事大學(xué)學(xué)報, 2010, 31(3): 68-73.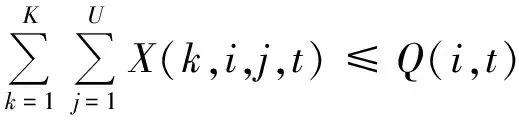
2 調(diào)度算法
2.1 最短距離優(yōu)先調(diào)度
2.2 窮舉路徑
2.3 堆場時間計算和配船方案
3 實 驗
3.1 實驗步驟
3.2 實驗結(jié)果
3.3 結(jié)果分析
4 總結(jié)和展望